快速入门
本章将介绍BDF的各种功能的基本使用,针对具体的计算功能给出基本的算例和数据读取分析说明。
第一个算例 \(\ce{H2O}\) 分子的RHF计算
Hartree-Fock是量子化学最基本算法。本小节,我们将通过一个水分子的Hartree-Fock计算例子,引导用户完成一个BDF计算并分析输入与输出信息。这里,我们先给出BDF的简洁输入,为了使用户理解BDF的简洁输入与高级输入模式的区别,我们也会给出每个简洁输入对应的高级输入文件。
准备输入
首先准备水分子单点能量Hartree-Fock计算的输入文件,命名为 h2o.inp, 输入内容如下:
#!bdf.sh
HF/3-21G
Geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # input bond length with the default unit angstrom
End geometry
- 输入解读如下:
第一行必须以
#!开始,跟着一个名为bdf.sh字符串,这个可以是任意的字母和数组字成字符串,不能包含除.外的特殊字符。第一行是系统保留行,用户可以利用这个字符串来标记计算任务。第二行
HF/3-21G是BDF的计算参数控制行,HF是Hartree-Fock的缩写,3-21G指定计算使用3-21G基组。关键参数控制行可以是连续的多行。第三行为空行,可忽略。这里输入是为了区分不同的输入内容,增强输入的可读性,建议用户保留。
第四行与第十行分别为
Geometry和End geometry,标记分子几何结构输入的起始与中止,坐标的默认单位是埃 (Angstrom)。第五行到第九行用内坐标的模式输入了水分子的结构。(详见 分子结构的内坐标格式输入)
这个简单的输入对应的BDF高级输入为:
$compass
Geometry
O
H 1 1.0
H 1 1.0 2 109.
End geometry
Basis
3-21g # set basis set as 3-21g
$end
$xuanyuan
$end
$scf
RHF # 限制性Hartree-Fock方法
Charge # 分子的电荷设置为0,默认计算中性分子,电荷为零
0
Spinmulti # 自旋多重度 2S+1,偶数电子体系默认计算单重态
1
$end
从高级输入可以看出,BDF将按顺序执行模块 COMPASS , XUANYUAN 和 SCF 完成水分子的单点能量计算。
COMPASS 用于读入分子结构,基函数等基本信息,判断分子的对称性,将分子转动到标准取向(Standard orientation,详见 BDF对群论的使用小节),产生对称匹配轨道等,
并将这些信息存入BDF的执行目录下的文件 h2o.chkfil 。 COMPASS 中的关键词
Geometry到End geometry之间定义的分子结构;
Basis定义基组为3-21G。
备注
只有在简洁输入中,才能用变量名(如上例中的R1)定义内坐标、定义完内坐标以后再给变量赋值。高级输入里的内坐标必须直接用数字定义,不支持使用变量。
执行完 COMPASS 模块后,BDF利用 XUANYUAN 模块计算单、双电子积分。由于BDF默认采用的是 重复计算双电子积分的SCF 方法,即 Integral Direct SCF 。
最后,BDF执行 SCF 模块,完成基于Hartree-Fock的自洽场计算。
RHF指定使用限制性Hartree-Fock方法;
Charge指定体系的电荷为0;
Spinmulti指定体系的自旋多重度为1。
这里 RHF 是必须输入的关键词, Charge 和 Spinmulti 对于限制性方法可以忽略。
执行计算
执行计算,需要准备一个Shell脚本,命名为 run.sh ,放入 输入文件 h2o.inp 所在的目录。内容如下:
#!/bin/bash
# 设置BDF的安装目录
export BDFHOME=/home/bsuo/bdf-pkg-pro
# 设置BDF的临时文件存放目录
export BDF_TMPDIR=/tmp/$RANDOM
# 设置可用堆区内存不受限,如果在超算环境计算,可能会受系统管理的限制
ulimit -s unlimitted
# 设定可用计算时间不受限,如果在超算环境计算,可能会受系统管理的限制
ulimit -t unlimitted
# 设置OpenMP并行线程数
export OMP_NUM_THREADS=4
# 设置OpenMP可用堆区内存大小
export OMP_STACKSIZE=1024M
# 执行BDF计算,注意,默认输出会打印至标准输出
$BDFHOME/sbin/bdfdrv.py -r h2o.inp
以上是 Bash Shell 脚本,定义了一些基本的环境变量,并利用 $BDFHOME/sbin/bdfdrv.py 执行计算。脚本中定义的环境变量有:
BDFHOME变量指定BDF的安装目录;
BDF_TMPDIR变量指定BDF运行时临时文件存放目录;
ulimit -s unlimitted设定程序可用的Stack区内存不受限;
ulimit -t unlimitted设定程序执行时间不受限;
export OMP_NUM_THREADS=4设定可用4个OpenMP线程执行并行计算;
export OMP_STACKSIZE=1024M设定OpenMP可用的Stack区内存为1024兆字节。
执行计算的命令为
$ ./run.sh h2o.inp &>h2o.out&
由于BDF将默认输出打印到标准输出,这里我们用了Linux的重定向命令,将标准输出定向到文件 h2o.out 。
计算结果分析
计算结束后,将得到 h2o.out , h2o.chkfil , h2o.scforb 等文件。
h2o.out是文本文件,用户可读,存储BDF输出打印信息;
h2o.chkfil是二进制文件,用户不可读,用于在BDF不同模块间传递数据;
h2o.scforb是文本文件,用户可读,存储了scf自洽迭代的分子轨道因子、轨道能等信息,主要用于重启动或作为其他scf计算的初始猜测轨道。
如果输入文件采用的是BDF简洁输入模式, h2o.out 中首先会给出一些基本的用户设置信息,
|================== BDF Control parameters ==================|
1: Input BDF Keywords
soc=None scf=rhf skeleton=True xcfuntype=None
xcfun=None direct=True charge=0 hamilton=None
spinmulti=1
2: Basis sets
['3-21g']
3: Wavefunction, Charges and spin multiplicity
charge=0 nuclearcharge=10 spinmulti=1
5: Energy method
scf
7: Acceleration method
ERI
8: Potential energy surface method
energy
|============================================================|
这里,
Input BDF Keywords给出了一些基本控制参数;
Basis set给出计算所用基组;
Wavefunction, Charges and spinmulti给出了体系电荷、总的核电荷数和自旋多重度(2S+1);
Energy method给出能量计算方法;
Accleration method给出双电子积分计算加速方法;
Potential energy surface method给出势能面计算方法,这里是单点能量计算。
随后,系统执行 COMPASS 模块,会给出如下提示:
|************************************************************|
Start running module compass
Current time 2021-11-18 11:26:28
|************************************************************|
然后打印输入的分子结构的笛卡尔坐标,单位为 Bohr ,以及每种类型原子的基函数详细信息
|---------------------------------------------------------------------------------|
Atom Cartcoord(Bohr) Charge Basis Auxbas Uatom Nstab Alink Mass
O 0.000000 0.000000 0.000000 8.00 1 0 0 0 E 15.9949
H 1.889726 0.000000 0.000000 1.00 2 0 0 0 E 1.0073
H -0.615235 1.786771 0.000000 1.00 2 0 0 0 E 1.0073
|----------------------------------------------------------------------------------|
End of reading atomic basis sets ..
Printing basis sets for checking ....
Atomic label: O 8
Maximum L 1 6s3p ----> 3s2p NBF = 9
#--->s function
Exp Coef Norm Coef Con Coef
322.037000 0.192063E+03 0.059239 0.000000 0.000000
48.430800 0.463827E+02 0.351500 0.000000 0.000000
10.420600 0.146533E+02 0.707658 0.000000 0.000000
7.402940 0.113388E+02 0.000000 -0.404454 0.000000
1.576200 0.355405E+01 0.000000 1.221562 0.000000
0.373684 0.120752E+01 0.000000 0.000000 1.000000
#--->p function
Exp Coef Norm Coef Con Coef
7.402940 0.356238E+02 0.244586 0.000000
1.576200 0.515227E+01 0.853955 0.000000
0.373684 0.852344E+00 0.000000 1.000000
Atomic label: H 1
Maximum L 0 3s ----> 2s NBF = 2
#--->s function
Exp Coef Norm Coef Con Coef
5.447178 0.900832E+01 0.156285 0.000000
0.824547 0.218613E+01 0.904691 0.000000
0.183192 0.707447E+00 0.000000 1.000000
随后,自动判断分子对称性,并根据用户设置决定是否转动为标准取向模式,
Auto decide molecular point group! Rotate coordinates into standard orientation!
Threshold= 0.10000E-08 0.10000E-11 0.10000E-03
geomsort being called!
gsym: C02V, noper= 4
Exiting zgeomsort....
Representation generated
Binary group is observed ...
Point group name C(2V) 4
User set point group as C(2V)
Largest Abelian Subgroup C(2V) 4
Representation generated
C|2|V| 2
Symmetry check OK
Molecule has been symmetrized
Number of symmery unique centers: 2
|---------------------------------------------------------------------------------|
Atom Cartcoord(Bohr) Charge Basis Auxbas Uatom Nstab Alink Mass
O 0.000000 0.000000 0.000000 8.00 1 0 0 0 E 15.9949
H 1.889726 0.000000 0.000000 1.00 2 0 0 0 E 1.0073
H -0.615235 1.786771 0.000000 1.00 2 0 0 0 E 1.0073
|----------------------------------------------------------------------------------|
Atom Cartcoord(Bohr) Charge Basis Auxbas Uatom Nstab Alink Mass
O 0.000000 -0.000000 0.219474 8.00 1 0 0 0 E 15.9949
H -1.538455 0.000000 -0.877896 1.00 2 0 0 0 E 1.0073
H 1.538455 -0.000000 -0.877896 1.00 2 0 0 0 E 1.0073
|----------------------------------------------------------------------------------|
细心的用户可能已经注意到,这里的水分子的坐标与输入的不一样。最后, COMPASS 会产生对称匹配轨道(Symmetry adapted orbital),并给出偶极矩和四极矩所属
的不可约表示,打印 C(2v) 点群的乘法表,给出总的基函数数目和每个不可约表示对称匹配轨道数目。
Number of irreps: 4
IRREP: 3 4 1
DIMEN: 1 1 1
Irreps of multipole moment operators ...
Operator Component Irrep Row
Dipole x B1 1
Dipole y B2 1
Dipole z A1 1
Quadpole xx A1 1
Quadpole xy A2 1
Quadpole yy A1 1
Quadpole xz B1 1
Quadpole yz B2 1
Quadpole zz A1 1
Generate symmetry adapted orbital ...
Print Multab
1 2 3 4
2 1 4 3
3 4 1 2
4 3 2 1
|--------------------------------------------------|
Symmetry adapted orbital
Total number of basis functions: 13 13
Number of irreps: 4
Irrep : A1 A2 B1 B2
Norb : 7 0 4 2
|--------------------------------------------------|
这里, C(2v) 点群有4个一维不可约表示,标记为 A1, A2, B1, B2 , 分别有 7, 0, 4, 2 个对称匹配的轨道。
注意
不同的量子化学软件,可能会采用不同的分子标准取向,导致某些分子轨道在不同程序中标记为不同的不可约表示。
最后, COMPASS 计算正常结束,会给出如下输出:
|******************************************************************************|
Total cpu time: 0.00 S
Total system time: 0.00 S
Total wall time: 0.02 S
Current time 2021-11-18 11:26:28
End running module compass
|******************************************************************************|
备注
BDF的每个模块执行,都会有开始执行和执行结束后打印时间信息,方便用户具体定位哪个计算模块出错。
本算例计算执行的第二个模块是 XUANYUAN , 该模块主要用于计算单、双电子积分。如果不特别指定,BDF默认采用直接计算双电子积分构造Fock矩阵的算法。这里, XUANYUAN 模块只计算和保存单电子积分及需要做积分预筛选的特殊双电子积分。如果用户在 compass 模块指定了 Saorb 关键词,双电子积分将被计算并保存到硬盘。 XUANYUAN 模块的输出比较简单,一般不需要特别关注。这里,我们给出最关键的输出:
[aoint_1e]
Calculating one electron integrals ...
S T and V integrals ....
Dipole and Quadupole integrals ....
Finish calculating one electron integrals ...
---------------------------------------------------------------
Timing to calculate 1-electronic integrals
CPU TIME(S) SYSTEM TIME(S) WALL TIME(S)
0.017 0.000 0.000
---------------------------------------------------------------
Finish calculating 1e integral ...
Direct SCF required. Skip 2e integral!
Set significant shell pairs!
Number of significant pairs: 7
Timing caluclate K2 integrals.
CPU: 0.00 SYS: 0.00 WALL: 0.00
从输出我们看到单电子重叠、动能与核吸引积分被计算,还计算了偶极矩和四极矩积分。由于输入要求默认的积分直接SCF计算(Direct SCF),双电子积分计算被忽略。
最后,BDF调用 SCF 模块执行 RHF 自洽场计算。需要关注的信息有:
Wave function information ...
Total Nuclear charge : 10
Total electrons : 10
ECP-core electrons : 0
Spin multiplicity(2S+1) : 1
Num. of alpha electrons : 5
Num. of beta electrons : 5
这里给出了核电荷数、总电子数、赝势计算的芯电子数、自旋多重度、alpha及beta电子数等信息,用户应当检查电子态是否正确。
然后, scf 模块先计算原子,并产生分子计算的初始猜测密度矩阵,
[ATOM SCF control]
heff= 0
After initial atom grid ...
Finish atom 1 O -73.8654283850
After initial atom grid ...
Finish atom 2 H -0.4961986360
Superposition of atomic densities as initial guess.
检查处理基函数可能的线性相关问题,
Check basis set linear dependence! Tolerance = 0.100000E-04
随后进入SCF迭代,8次迭代收敛后关闭 DIIS 和 Level shift 等加速收敛方法并重新计算能量,
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -75.465225043 -0.607399386 0.039410497 0.238219747 0.0000 0.00
2 1 0.000 -75.535887715 -0.070662672 0.013896819 0.080831047 0.0000 0.00
3 2 0.000 -75.574187153 -0.038299437 0.004423591 0.029016074 0.0000 0.00
4 3 0.000 -75.583580885 -0.009393732 0.000961664 0.003782740 0.0000 0.00
5 4 0.000 -75.583826898 -0.000246012 0.000146525 0.000871203 0.0000 0.00
6 5 0.000 -75.583831666 -0.000004768 0.000012300 0.000073584 0.0000 0.00
7 6 0.000 -75.583831694 -0.000000027 0.000001242 0.000007487 0.0000 0.00
8 7 0.000 -75.583831694 -0.000000000 0.000000465 0.000002549 0.0000 0.00
diis/vshift is closed at iter = 8
9 0 0.000 -75.583831694 -0.000000000 0.000000046 0.000000221 0.0000 0.00
Label CPU Time SYS Time Wall Time
SCF iteration time: 0.017 S 0.017 S 0.000 S
最后打印不同项的能量贡献和维里比。
Final scf result
E_tot = -75.58383169
E_ele = -84.37566837
E_nn = 8.79183668
E_1e = -121.94337426
E_ne = -197.24569473
E_kin = 75.30232047
E_ee = 37.56770589
E_xc = 0.00000000
Virial Theorem 2.003738
根据维里定律(Virial Theorem),对于非相对论系统,系统的总势能的绝对值是电子的动能的2倍,这里的维里比是 2.003738 。 系统的能量为:
E_tot是系统总能量,即E_ele+E_nn;
E_ele是电子能量,即E_1e+E_ee+E_xc;
E_nn是原子核排斥能;
E_1e是单电子能量,即E_ne+E_kin;
E_ne是原子核对电子的吸引能;
E_kin是电子动能;
E_ee是双电子能,包括库伦排斥和交换能;
E_xc是交换相关能,DFT计算时不为0.
能量打印后输出的是轨道的占据情况、轨道能、HUMO-LOMO能量和能隙等信息,如下所示:
[Final occupation pattern: ]
Irreps: A1 A2 B1 B2
detailed occupation for iden/irep: 1 1
1.00 1.00 1.00 0.00 0.00 0.00 0.00
detailed occupation for iden/irep: 1 3
1.00 0.00 0.00 0.00
detailed occupation for iden/irep: 1 4
1.00 0.00
Alpha 3.00 0.00 1.00 1.00
[Orbital energies:]
Energy of occ-orbs: A1 3
-20.43281195 -1.30394125 -0.52260024
Energy of vir-orbs: A1 4
0.24980046 1.23122290 1.86913815 3.08082943
Energy of occ-orbs: B1 1
-0.66958992
Energy of vir-orbs: B1 3
0.34934415 1.19716413 2.03295437
Energy of occ-orbs: B2 1
-0.47503768
Energy of vir-orbs: B2 1
1.78424252
Alpha HOMO energy: -0.47503768 au -12.92643838 eV Irrep: B2
Alpha LUMO energy: 0.24980046 au 6.79741929 eV Irrep: A1
HOMO-LUMO gap: 0.72483814 au 19.72385767 eV
这里
[Final occupation pattern: ]给出的是轨道占据情况。由于我们进行的是限制性Hartree-Fock计算,占据情况只给出了Alpha轨道的信息,按照不可约表示分别给出。从这个例子可以看出,A1轨道的前3个、B1和B2轨道的第1个分别有1个电子占据。由于本算例是RHF,alpha与beta轨道是一样的,所以A1表示有3个双占据轨道,B1和B2表示分别有1个双占据轨道。
[Orbital energies:]按照不可约表示分别给出轨道能;
Alpha HOMO energy:按照单位 au 和 eV 给出了HOMO轨道能;该轨道所属的不可约表示,这里是B2;
Alpha LUMO energy:按照单位 au 和 eV 给出了LUMO轨道能;该轨道所属的不可约表示,这里是A1;
HOMO-LUMO gap:给出HOMO和LUMO轨道的能差。
为了减少输出行数,BDF默认不打印轨道成分及分子轨道系数,只按照不可约表示分类给出部分轨道占据数和轨道能信息,如下:
Symmetry 1 A1
Orbital 1 2 3 4 5 6
Energy -20.43281 -1.30394 -0.52260 0.24980 1.23122 1.86914
Occ No. 2.00000 2.00000 2.00000 0.00000 0.00000 0.00000
Symmetry 2 A2
Symmetry 3 B1
Orbital 8 9 10 11
Energy -0.66959 0.34934 1.19716 2.03295
Occ No. 2.00000 0.00000 0.00000 0.00000
Symmetry 4 B2
Orbital 12 13
Energy -0.47504 1.78424
Occ No. 2.00000 0.00000
SCF 模块最后打印的是Mulliken和Lowdin布居分析的结果,分子的偶极矩信息。
[Mulliken Population Analysis]
Atomic charges:
1O -0.7232
2H 0.3616
3H 0.3616
Sum: -0.0000
[Lowdin Population Analysis]
Atomic charges:
1O -0.4756
2H 0.2378
3H 0.2378
Sum: -0.0000
[Dipole moment: Debye]
X Y Z
Elec:-.1081E-64 0.4718E-32 -.2368E+01
Nucl:0.0000E+00 0.0000E+00 0.5644E-15
Totl: -0.0000 0.0000 -2.3684
高斯基组
为了求解Hartree-Fock、Kohn-Sham DFT方程,需要把分子轨道展开为单电子基函数的线性组合:
在量子化学的计算中,基函数只有数学意义,没有物理意义。基函数越多则结果越精确,但是也取决于怎么合理地设置基函数。当基函数无穷多,称为完备集,就达到了完备基组极限(Complete Basis Set Limit, CBS),能够完美展开分子轨道。实际用的是有限基组,达不到CBS,由此导致的计算结果的误差称为基组不完备性误差。
用多少基函数,就会产生多少分子轨道,但是只有占据轨道,以及低阶的非占据轨道(价层空轨道)通常有化学意义。如果基函数取的就是原子轨道,称为原子轨道线性组合(linear combination of atomic orbitals,LCAO),但是这只是结构化学上的概念,实际计算中使用的基函数并不是真实的原子轨道。
量子化学中常用的基函数如下:
高斯轨道(Gauss type orbital, GTO)基函数:因其在数学形式上易于计算双电子积分,绝大多数量子化学程序使用的都是GTO基函数。
Slater轨道(Slater type orbital, STO)基函数:半经验以及少数量子化学程序(如ADF)所用的基函数。难以计算双电子积分,但相对于GTO基函数,它的径向行为更接近于实际原子轨道,因此只需要较少数目的STO就可以达到较多数目GTO的计算结果。
平面波(Plane wave):专门适用于周期性计算的基函数,计算孤立体系时比GTO基函数性价比低得多。
数值原子轨道(Numerical atomic orbital, NAO)基函数:极少程序支持,典型的是Dmol3、Siesta。NAO基函数并没有解析的数学形式,而是通过离散分布的点描述。
BDF软件早期采用STO基函数,目前主要采用GTO基函数。
对于轨道角动量 L 高于 p 的GTO基函数(如 d 、f 等GTO基函数),有两种表示方式。 一种写为笛卡尔函数(也称直角函数)形式:
它有 \((L+1)(L+2)/2\) 个分量,例如 d 函数包含xx,yy,zz,xy,xz,yz。另一种写为球函数(也称球谐函数、纯函数)形式:
它有 \(2L+1\) 个分量,例如 d 函数包含-2,-1,0,+1,+2。
笛卡尔函数的优点是容易计算积分,但是存在冗余函数;而球函数恰好与 \(2L+1\) 个磁量子数相对应, 因此在量子化学程序中通常先在笛卡尔函数下计算积分,然后通过一定的线性关系 [53] ,组合成球函数的积分。
注意
除Pople型等较早的基组外,大多数现代高斯基组都是在球基函数下优化的。
笛卡尔基函数无论在精度上还是在效率上均无优势,尤其是对于全电子相对论计算还会导致数值不稳定,因此在BDF计算中一律采用球基函数。
笛卡尔基函数和球基函数会导致不同的结果。如果用其它量子化学程序重复BDF的计算结果,除保证结构、方法、基组相同外,还需检查是否用了球基函数。
在很多文献中,人们把各种原子在不同情形下优化好的GTO基函数做成数据集(data set),并赋以不同的名称供量子化学程序调用。这些命名的GTO基函数数据集称为 高斯基组 (Gaussian Basis Sets)。 BDF内置的高斯基组主要来自以下基组库网站,各种基组的原始文献可以在相应的网站中找到。
Basis Set Exchange [54] :全电子基组,标量ECP基组,可以输出BDF格式(注意:ECP基组要手动调整ECP数据的位置)。 https://www.basissetexchange.org/
Stuttgart/Cologne赝势基组库:主要是SOECP基组和“f-in-core”基组,以及少量早期的标量ECP基组。 http://www.tc.uni-koeln.de/PP/clickpse.en.html
Turbomole基组库:全电子基组,标量ECP基组,SOECP基组。 http://www.cosmologic-services.de/basis-sets/basissets.php
Dyall相对论基组:全电子相对论基组。 http://dirac.chem.sdu.dk/basisarchives/dyall/index.html
Sapporo基组库:全电子基组。 http://sapporo.center.ims.ac.jp/sapporo/
Clarkson大学ECP基组库:SOECP基组。 https://people.clarkson.edu/~pchristi/reps.html
ccECP基组库:标量ECP基组;Kr之后是SOECP基组。 https://pseudopotentiallibrary.org/
Molpro基组库:全电子基组,ECP基组(不显示ECP参数)。 https://www.molpro.net/
ccRepo基组库:收录了最新开发的关联一致基组,包括全电子非相对论,全电子相对论,SOECP基组(不显示ECP参数),和密度拟合等多种类型。 http://www.grant-hill.group.shef.ac.uk/ccrepo/
此外,有个别元素的内置基组来自原始文献:
全电子基组Dirac-RPF-4Z和Dirac-aug-RPF-4Z,包括s-、p-区元素 [55],d-区元素 [56],f-区元素 [57]
Ga—Kr的全电子DKH2收缩基组(aug-)cc-p(w)CVnZ-DK未被Basis Set Exchange收录,取自原始文献 [58]
赝势基组Pitzer-AVDZ-PP、Pitzer-VDZ-PP、Pitzer-VTZ-PP [59]
赝势基组CRENBL中的 Ce - Lu [60] ,Fr - Pu [61] ,Am - Og [62, 63] (注意:Basis Set Exchange上的Am - Og基组是错的!)
赝势基组CRENBS中的 Am - Og [62, 63] (注意:Basis Set Exchange上的Am - Og基组是错的!)
BDF用户既可以使用BDF基组库中的标准基组,也可以使用自定义基组。
全电子基组
全电子基组分为非收缩基组与收缩基组两类。前者既可用于非相对论计算也可用于相对论计算,但主要是相对论计算,而后者又分为非相对论收缩基组和相对论收缩基组。
全电子相对论计算要用到DKH、ZORA、X2C等考虑相对论效应的哈密顿(见 相对论效应 ), 此时必须要用专门为相对论计算优化的收缩基组,比如cc-pVnZ-DK系列、SARC、ANO-RCC等等。 大多数相对论收缩基组把原子核作为点电荷处理,但是有些基组在做收缩时考虑了原子核分布尺寸效应,这对 s 、 p 基函数的收缩因子影响最为明显。 相应地,在分子积分的计算中也必须采用 有限核模型 。
基组类型 |
基组名称 |
支持的元素 |
备注 |
|---|---|---|---|
Pople |
STO-3G
STO-6G
|
1- 54 |
|
3-21G
|
1- 55 |
||
3-21++G
|
1, 3- 20 |
||
6-31G
6-31G(d,p)
6-31GP
6-31GPP
|
1- 36 |
||
6-31++G
6-31++GP
6-31++GPP
6-31+G
6-31+GP
6-31+GPP
|
1- 20 |
||
6-31G(2df,p)
6-31G(3df,3pd)
|
1- 18 |
||
6-311++G
6-311++G(2d,2p)
6-311++GP
6-311++GPP
|
1, 3- 20 |
||
6-311+G
6-311+G(2d,p)
6-311+GP
6-311+GPP
|
1- 20 |
||
6-311G
6-311G(d,p)
6-311GP
6-311GPP
|
1- 20, 31- 36, 53 |
||
6-31++GPP-J
6-31+GP-J
6-31G-J
6-311++GPP-J
6-311+GP-J
6-311G-J
|
1, 6- 8 |
||
6-311G(2df,2pd)
|
1- 10, 19- 20 |
||
6-311++G(3df,3pd)
|
1, 3- 18 |
||
关联一致 |
aug-cc-pVDZ
aug-cc-pVTZ
aug-cc-pVQZ
aug-cc-pV5Z
|
1- 18, 21- 36 |
|
cc-pVDZ
cc-pVTZ
cc-pVQZ
cc-pV5Z
|
1- 18, 20- 36 |
||
aug-cc-pV6Z
cc-pV6Z
|
1- 2, 5- 10, 13- 18 |
||
aug-cc-pV7Z
|
5- 10 |
||
aug-cc-pCVDZ
aug-cc-pCVTZ
aug-cc-pCVQZ
aug-cc-pCV5Z
aug-cc-pCV6Z
|
D: 1- 18, 31-36
T: 1- 18, 31-36
Q: 1- 18, 31-36
5: 5- 18, 31-36
6: 5- 10, 13-18
|
||
cc-pCVDZ
cc-pCVTZ
cc-pCVQZ
cc-pCV5Z
cc-pCV6Z
|
D: 1- 18, 20, 31-36
T: 1- 18, 20, 31-36
Q: 1- 18, 20, 31-36
5: 5- 18, 31-36
6: 5- 10, 13-18
|
||
aug-cc-pV(D+d)Z
aug-cc-pV(T+d)Z
aug-cc-pV(Q+d)Z
aug-cc-pV(5+d)Z
|
1- 18, 21- 36 |
||
cc-pV(D+d)Z
cc-pV(T+d)Z
cc-pV(Q+d)Z
cc-pV(5+d)Z
|
1- 18, 20- 36 |
||
aug-cc-pwCVDZ
aug-cc-pwCVTZ
aug-cc-pwCVQZ
aug-cc-pwCV5Z
|
D: 5- 10, 13- 20, 31- 36
T: 5- 10, 13- 36
Q: 5- 10, 13- 36
5: 5- 10, 13- 18, 21- 36
|
||
cc-pwCVDZ
cc-pwCVTZ
cc-pwCVQZ
cc-pwCV5Z
|
D: 5- 10, 13- 20, 31- 36
T: 5- 10, 13- 36
Q: 5- 10, 13- 36
5: 5- 10, 13- 18, 21- 36
|
||
aug-cc-pVDZ-RIFIT
aug-cc-pVTZ-RIFIT
aug-cc-pVQZ-RIFIT
|
1- 2, 4- 10, 12- 18, 21- 36 |
辅助基组 |
|
aug-cc-pV5Z-RIFIT
aug-cc-pV6Z-RIFIT
|
5: 1- 10, 13- 18, 21- 36
6: 1- 2, 5- 10, 13- 18
|
辅助基组 |
|
aug-cc-pVTZ-J
|
1, 5- 9, 13- 17, 21- 30, 34 |
辅助基组 |
|
aug-cc-pVDZ-DK
aug-cc-pVTZ-DK
aug-cc-pVQZ-DK
aug-cc-pV5Z-DK
|
D: 1- 18, 21- 36
T: 1- 54, 72- 86
Q: 1- 18, 21- 36
5: 1- 2, 5- 10, 13- 18, 21- 36
|
相对论 |
|
aug-cc-pCVDZ-DK
aug-cc-pCVTZ-DK
aug-cc-pCVQZ-DK
aug-cc-pCV5Z-DK
|
D: 3- 18, 31-36
T: 3- 18, 31-36
Q: 3- 18, 31-36
5: 5- 10, 13-18, 31-36
|
相对论 |
|
aug-cc-pwCVDZ-DK
aug-cc-pwCVTZ-DK
aug-cc-pwCVQZ-DK
aug-cc-pwCV5Z-DK
|
D: 5-10, 13-20, 31-38
T: 5-10, 13-20, 21-38, 39-54, 72-86
Q: 5-10, 13-20, 21-38, 49-54, 81-86
5: 5-10, 13-18, 21-36
|
相对论 |
|
aug-cc-pVDZ-DK3
aug-cc-pVTZ-DK3
aug-cc-pVQZ-DK3
aug-cc-pwCVDZ-DK3
aug-cc-pwCVTZ-DK3
aug-cc-pwCVQZ-DK3
|
D: 55- 56, 87- 88
T: 49- 56, 72- 88
Q: 49- 56, 81- 88
|
相对论 |
|
aug-cc-pCVDZ-X2C
aug-cc-pCVTZ-X2C
aug-cc-pCVQZ-X2C
aug-cc-pCV5Z-X2C
aug-cc-pCV6Z-X2C
|
5- 10, 13- 18 |
相对论 |
|
aug-cc-pVDZ-X2C
aug-cc-pVTZ-X2C
aug-cc-pVQZ-X2C
|
1- 2, 5- 10, 13- 20, 37- 38, 55- 56,
87- 88
|
相对论 |
|
aug-cc-pV5Z-X2C
aug-cc-pV6Z-X2C
|
1- 2, 5- 10, 13- 18 |
相对论 |
|
aug-cc-pwCVDZ-X2C
aug-cc-pwCVTZ-X2C
aug-cc-pwCVQZ-X2C
|
5- 10, 13- 20, 37- 38, 55- 56, 87- 88 |
相对论 |
|
aug-cc-pwCV5Z-X2C
|
5- 10, 13- 18 |
相对论 |
|
cc-pVDZ-DK
cc-pVTZ-DK
cc-pVQZ-DK
cc-pV5Z-DK
|
D: 1- 18, 21- 36
T: 1- 54, 72- 86
Q: 1- 18, 21- 36
5: 1- 18, 21- 36
|
相对论 |
|
cc-pCVDZ-DK
cc-pCVTZ-DK
cc-pCVQZ-DK
cc-pCV5Z-DK
|
D: 3- 18, 31-36
T: 3- 18, 31-36
Q: 3- 18, 31-36
5: 5- 10, 13-18, 31-36
|
相对论 |
|
cc-pwCVDZ-DK
cc-pwCVTZ-DK
cc-pwCVQZ-DK
cc-pwCV5Z-DK
|
D: 5-10, 13-20, 31-38
T: 5-10, 13-20, 21-38, 39-54, 72-86
Q: 5-10, 13-20, 21-38, 49-54, 81-86
5: 5-10, 13-18, 21-36
|
相对论 |
|
cc-pVDZ-DK3
cc-pVTZ-DK3
cc-pVQZ-DK3
cc-pwCVDZ-DK3
cc-pwCVTZ-DK3
cc-pwCVQZ-DK3
|
D: 55- 71, 87-103
T: 49-103
Q: 49- 71, 81-103
|
相对论 |
|
cc-pCVDZ-X2C
cc-pCVTZ-X2C
cc-pCVQZ-X2C
cc-pCV5Z-X2C
cc-pCV6Z-X2C
|
5- 10, 13- 18 |
相对论 |
|
cc-pVDZ-X2C
cc-pVTZ-X2C
cc-pVQZ-X2C
|
1-2, 5-10, 13-20, 37-38, 55-71,
87-103
|
相对论 |
|
cc-pV5Z-X2C
cc-pV6Z-X2C
|
1- 2, 5- 10, 13- 18 |
相对论 |
|
cc-pwCVDZ-X2C
cc-pwCVTZ-X2C
cc-pwCVQZ-X2C
|
5- 10, 13- 20, 37- 38, 55- 71,
87-103
|
相对论 |
|
cc-pwCV5Z-X2C
|
5-10, 13-18 |
相对论 |
|
cc-pVDZ-FW_fi
cc-pVTZ-FW_fi
cc-pVQZ-FW_fi
cc-pV5Z-FW_fi
|
1-2, 5-10, 13-18, 31-36 |
相对论,有限核 |
|
cc-pVDZ-FW_pt
cc-pVTZ-FW_pt
cc-pVQZ-FW_pt
cc-pV5Z-FW_pt
|
1-2, 5-10, 13-18, 31-36 |
相对论 |
|
ANO |
ADZP-ANO
|
1-103 |
|
ANO-DK3
|
1- 10 |
相对论 |
|
ANO-R
ANO-R0
ANO-R1
ANO-R2
ANO-R3
|
1- 86
R: full; R0: MB;
R1: VDZP; R2: VTZP;
R3: VQZP
|
相对论,有限核;
2021年修订版;
2020版加后缀-old
|
|
ANO-RCC
ANO-RCC-VDZ
ANO-RCC-VDZP
ANO-RCC-VTZP
ANO-RCC-VQZP
|
1- 96 |
相对论 |
|
ANO-RCC-VTZ
|
3- 20, 31- 38 |
相对论 |
|
Ahlrichs |
Def2系列
|
全电子非相对论基组与赝势基组的混合,见 赝势基组 |
|
jorge-DZP
jorge-TZP
jorge-QZP
|
D: 1-103
T: 1-103
Q: 1- 54
|
||
jorge-DZP-DKH
jorge-TZP-DKH
jorge-QZP-DKH
|
D: 1-103
T: 1-103
Q: 1- 54
|
相对论,有限核 |
|
SARC-DKH2
|
57- 86, 89-103 |
相对论 |
|
SARC2-QZV-DKH2
SARC2-QZVP-DKH2
|
57- 71 |
相对论 |
|
x2c-SV(P)all
x2c-SVPall
x2c-TZVPall
x2c-TZVPPall
x2c-QZVPall
x2c-QZVPPall
x2c-SV(P)all-2c
x2c-SVPall-2c
x2c-TZVPall-2c
x2c-TZVPPall-2c
x2c-QZVPall-2c
x2c-QZVPPall-2c
|
1- 86 |
相对论,有限核 |
|
Sapporo |
Sapporo-DZP
Sapporo-TZP
Sapporo-QZP
Sapporo-DZP-2012
Sapporo-TZP-2012
Sapporo-QZP-2012
Sapporo-DZP-dif
Sapporo-TZP-dif
Sapporo-QZP-dif
Sapporo-DZP-2012-dif
Sapporo-TZP-2012-dif
Sapporo-QZP-2012-dif
|
1- 54 |
2012是新版 |
Sapporo-DKH3-DZP
Sapporo-DKH3-TZP
Sapporo-DKH3-QZP
Sapporo-DKH3-DZP-dif
Sapporo-DKH3-TZP-dif
Sapporo-DKH3-QZP-dif
|
1- 54 |
相对论 |
|
Sapporo-DKH3-DZP-2012
Sapporo-DKH3-TZP-2012
Sapporo-DKH3-QZP-2012
Sapporo-DKH3-DZP-2012-dif
Sapporo-DKH3-TZP-2012-dif
Sapporo-DKH3-QZP-2012-dif
|
19- 86 |
相对论,有限核 |
|
非收缩 |
UGBS
|
1- 90, 94- 95, 98-103 |
相对论 |
Dirac-RPF-4Z
Dirac-aug-RPF-4Z
|
1-118 |
相对论 |
|
Dirac-Dyall.2zp
Dirac-Dyall.3zp
Dirac-Dyall.4zp
Dirac-Dyall.ae2z
Dirac-Dyall.ae3z
Dirac-Dyall.ae4z
Dirac-Dyall.cv2z
Dirac-Dyall.cv3z
Dirac-Dyall.cv4z
Dirac-Dyall.v2z
Dirac-Dyall.v3z
Dirac-Dyall.v4z
|
1-118 |
相对论 |
|
Dirac-Dyall.aae2z
Dirac-Dyall.aae3z
Dirac-Dyall.aae4z
Dirac-Dyall.acv2z
Dirac-Dyall.acv3z
Dirac-Dyall.acv4z
Dirac-Dyall.av2z
Dirac-Dyall.av3z
Dirac-Dyall.av4z
|
1-2, 5-10, 13-18, 31-36, 49-54
81-86, 113-118
|
相对论 |
|
其它 |
SVP-BSEX
|
1, 3-10 |
|
DZP
|
1, 6-8, 16, 26, 42 |
||
DZVP
|
1, 3-9, 11-17, 19-20, 31-35, 49-53 |
||
TZVPP
|
1, 6-7 |
||
IGLO-II
IGLO-III
|
1, 5- 9, 13- 17 |
||
Sadlej-pVTZ
|
1, 6- 8 |
||
Wachters+f
|
21- 29 |
||
赝势基组
有效芯势(Effective Core Potential, ECP)包括赝势(Pseudopotential, PP)和模型芯势(Model Core Potential, MCP)。 量子化学计算中的PP与平面波计算中的PP并无本质差别,只不过表示为简明的解析式形式。 包括BDF在内的大部分量子化学软件都支持PP,而支持MCP的量子化学软件较少,因此在不引起歧义的情况下,ECP与PP两个名称可以混用。
赝势基组需要结合赝势使用,基函数只描述原子的价层电子。当体系涉及到比较重的原子时,可以对它们用赝势基组, 而其它原子照常用普通的非相对论全电子基组。 在重元素较多的情况下,这样一方面可以大大节约计算时间,同时还能等效体现出标量相对论效应。Lan系列、Stuttgart系列、cc-pVnZ-PP系列都属于这类基组。 为了方便调用,一些较轻元素的赝势基组实际上是非相对论全电子基组,如第五周期之前元素的Def2系列基组。
根据赝势是否包含旋轨耦合项,赝势基组分为标量赝势基组与旋轨耦合赝势(SOECP)基组两类。
基组类型 |
基组名称 |
支持的元素 |
备注 |
|---|---|---|---|
关联一致 |
aug-cc-pVDZ-PP
aug-cc-pVTZ-PP
aug-cc-pVQZ-PP
aug-cc-pV5Z-PP
aug-cc-pwCVDZ-PP
aug-cc-pwCVTZ-PP
aug-cc-pwCVQZ-PP
aug-cc-pwCV5Z-PP
cc-pV5Z-PP
cc-pwCV5Z-PP
|
29- 36, 39- 54, 72- 86 |
SOECP |
cc-pVDZ-PP
cc-pVTZ-PP
cc-pVQZ-PP
cc-pwCVDZ-PP
cc-pwCVTZ-PP
cc-pwCVQZ-PP
|
29- 36, 39- 54, 72- 86, 90- 92 |
SOECP |
|
aug-cc-pCVDZ-ccECP
aug-cc-pCVTZ-ccECP
aug-cc-pCVQZ-ccECP
aug-cc-pCV5Z-ccECP
cc-pCVDZ-ccECP
cc-pCVTZ-ccECP
cc-pCVQZ-ccECP
cc-pCV5Z-ccECP
|
19- 30, 42, 46, 47, 74, 77, 79 |
SOECP (Z > 36) |
|
aug-cc-pVDZ-ccECP
aug-cc-pVTZ-ccECP
aug-cc-pVQZ-ccECP
aug-cc-pV5Z-ccECP
aug-cc-pV6Z-ccECP
|
D/T/Q/5: 3- 9, 11- 17, 19- 36,
42, 46, 47, 52, 53, 74, 77, 79,
83
6: 4- 9, 12- 17, 19- 20, 31- 36,
52, 53, 83
|
SOECP (Z > 36) |
|
cc-pVDZ-ccECP
cc-pVTZ-ccECP
cc-pVQZ-ccECP
cc-pV5Z-ccECP
cc-pV6Z-ccECP
|
D/T/Q/5: 3- 36, 42, 46, 47, 52, 53,
74, 77, 79, 83
6: 4- 10, 12- 20, 31- 36, 52, 53, 83
|
SOECP (Z > 36) |
|
Pitzer-AVDZ-PP
|
3- 10 |
SOECP |
|
Pitzer-VDZ-PP
Pitzer-VTZ-PP
|
3- 18 |
SOECP |
|
Clarkson |
CRENBL
|
1 (全电子), 3-118 |
SOECP,小芯 |
CRENBS
|
21- 36, 39- 54, 57, 72- 86,
104-118
|
SOECP,大芯 |
|
Ahlrichs |
Def2-SVP-old
Def2-SV(P)-old
Def2-SVPD-old
Def2-TZVP-old
Def2-TZVPD-old
Def2-TZVP-F-old
Def2-TZVPP-F-old
Def2-TZVPP-old
Def2-TZVPPD-old
Def2-QZVP-old
Def2-QZVPD-old
Def2-QZVPP-old
Def2-QZVPPD-old
Def2-SV(P)-G16
Def2-SVP-G16
Def2-TZVP-G16
Def2-TZVPP-G16
Def2-QZVP-G16
Def2-QZVPP-G16
Def2-SVPD
Def2-TZVPD
Def2-TZVPPD
Def2-QZVPD
Def2-QZVPPD
ma-Def2-SV(P)
ma-Def2-SVP
ma-Def2-TZVP
ma-Def2-TZVPP
ma-Def2-QZVP
ma-Def2-QZVPP
|
1- 36 (全电子), 37- 57, 72- 86 |
-old是旧版
-G16采用完整赝势
|
Def2-SV(P)
Def2-SVP
Def2-TZVP
Def2-TZVPP
Def2-TZVP-F
Def2-TZVPP-F
Def2-QZVP
Def2-QZVPP
|
1- 36 (全电子), 37- 86 |
||
DHF-SV(P)
DHF-SVP
DHF-TZVP
DHF-TZVPP
DHF-QZVP
DHF-QZVPP
|
37- 56, 72- 86 |
SOECP |
|
LAN |
LANL2DZ
|
1, 3-10 (全电子)
11-57, 72-83, 92-94
|
|
LANL2DZDP
|
1, 6-9 (全电子)
14-17, 32-35, 50-53, 82-83
|
||
LANL2TZ
|
21- 30, 39- 48, 57, 72- 80 |
||
LANL08
|
11- 57, 72- 83 |
||
LANL08(D)
|
14- 17, 32- 35, 50- 53, 82- 83 |
||
LANL2TZ+
LANL08+
|
21- 30 |
||
Modified-LANL2DZ
LANL2TZ(F)
LANL08(F)
|
21- 29, 39- 47, 57, 72- 79 |
||
SBKJC |
SBKJC-VDZ
|
1-2 (全电子), 3- 58, 72- 86 |
|
SBKJC-POLAR
|
1-2 (全电子)
3- 20, 32- 38, 50- 56, 82- 86
|
||
pSBKJC
|
6- 9, 14- 17, 32- 35, 50- 53 |
||
Stuttgart |
Stuttgart-RLC
|
3- 20, 30- 38, 49- 56, 80- 86
89-103
|
大芯 |
SDB-cc-pVTZ
SDB-cc-pVQZ
|
31- 36, 49- 54 |
大芯 |
|
SDB-aug-cc-pVTZ
SDB-aug-cc-pVQZ
|
31- 35, 49- 53 |
大芯 |
|
Stuttgart-RSC-1997
|
19-30, 37-48, 55-56, 58-70
72-80, 89-103, 105
|
小芯 |
|
Stuttgart-RSC-ANO
Stuttgart-RSC-SEG
|
57- 71, 89-103 |
SOECP,小芯 |
|
Stuttgart-ECP92MDFQ-DZVP
Stuttgart-ECP92MDFQ-TZVP
Stuttgart-ECP92MDFQ-QZVP
|
111-120 |
SOECP,小芯 |
|
Stuttgart-ECPMDFSO-QZVP
|
19- 20, 37- 38, 55- 56, 87- 92 |
SOECP,小芯 |
备注
关于Def2系列基组
Def2系列基组是采用Turbomole程序开发的,“Def2”表示该程序的“第二套默认基组”。
原始的Def2系列基组(后缀 -old)存在一些缺陷,在Turbomole 7.3之后版本的Def2基组中作了修正,包括: Ba增加了f极化函数(个别QZ基组还增加了g函数);对Def2-QZVPD和Def2-QZVPPD重新优化了I的f、g函数;Def2-QZVPPD补充了Mn缺失的f函数; 部分Def2基组支持镧系原子。
Def2基组对Kr之后的原子采用Stuttgart/Cologne赝势。由于当时的Turbomole程序不支持高角动量赝势,故对赝势做了截断,并沿用至今。 这会导致0.1 — 1 mHartree量级的能量差。而在Gaussian 16程序中,使用了标准的Stuttgart/Cologne赝势(用后缀 -G16 加以区分)。
通常情况下用Def2-…或Def2-…-G16均可,旋轨耦合计算可以用SOECP版本的DHF-…基组。 在涉及Kr之后原子的情况下,如果想重复Gaussian 16程序Def2系列基组的计算结果,必须用Def2-…-G16基组。 不建议使用原始的Def2-…-old基组,除非为了重复涉及Mn、I、Ba原子的早期计算结果。
除了以上的赝势基组,对于镧系、锕系原子还有一种把f电子放入赝势的“f-in-core”(FIC)基组。 目前BDF的基组库包含以下FIC标量赝势基组,适用于镧系、锕系原子常见氧化态的成键情况。 在拟合赝势参数的参考数据集中,已经对多个低能级在Wood-Boring近似下考虑了标量相对论效应(MWB)。
基组名称 |
支持的元素 |
芯电子 |
|---|---|---|
MWB-FIC
MWB-FIC-I
MWB-FIC-II
|
57- 71
|
[Kr](4d)10(4f)n
|
MWB-FIC-AVDZ
MWB-FIC-AVTZ
MWB-FIC-AVQZ
|
89-103
|
[Xe](4f)14(5d)10(5f)n
|
MWB-FICp1
|
57- 70
|
[Kr](4d)10(4f)n+1
|
MWB-FICp1-AVDZ
MWB-FICp1-AVTZ
MWB-FICp1-AVQZ
|
94-102
|
[Xe](4f)14(5d)10(5f)n+1
|
MWB-FICm1-AVDZ
MWB-FICm1-AVTZ
MWB-FICm1-AVQZ
|
58- 60, 65, 66,
90- 98
|
[Kr](4d)10(4f)n-1,
[Xe](4f)14(5d)10(5f)n-1
|
MWB-FICm2-AVDZ
MWB-FICm2-AVTZ
MWB-FICm2-AVQZ
|
91- 95
|
[Xe](4f)14(5d)10(5f)n-2
|
MWB-FICm3-AVDZ
MWB-FICm3-AVTZ
MWB-FICm3-AVQZ
|
92
|
[Xe](4f)14(5d)10(5f)n-3
|
标准基组的别名和缩写
基组库中的基组除了使用以上的标准名称之外,部分基组也可以使用其别名及缩写。基本规则如下:
6-系列的Pople基组中,代表极化函数的后缀 P、PP 可以用星号表示。例如,6-311++G** 等同于 6-311++GPP。
def2-系列基组的连字符 “ - ” 可以省略。例如,def2-SVP 可以写为 def2SVP。
在关联一致基组中,“cc-pV”、“cc-pCV”、”cc-pwCV”可以分别简写为 V、CV、WCV, 表示弥散函数的前缀 “aug-” 可缩写为 A(不区分大小写)。 例如,vdz 表示 cc-pVDZ,awcvtz-dk 表示 aug-cc-pwCVTZ-DK, 等等。需要注意的是,这种基组名的缩写仅限用于BDF的输入, 不要用在正式的论文和报告中,以免造成读者困惑。
自定义基组文件
BDF可以使用非内置基组,此时要把基组数据保存在文本格式的基组文件中,放在计算目录下,文件名就是BDF中要引用的基组名。
警告
自定义基组文件的文件名必须 全部大写 !但在输入文件中引用时,大小写任意。
例如,在计算目录下创建一个文本文件MYBAS-1(注意:如果在Windows操作系统下创建文本文件,系统可能会隐去扩展名 .txt ,因此实际名称是MYBAS-1.txt),内容为:
# This is my basis set No. 1. # 任意的空行,以及 # 打头的注释行
# Supported elements: He and Al
**** # 4个星号打头的行,接下来是一个元素的基组
He 2 1 # 元素符号,核电荷数,基函数的最高角动量+1
S 4 2 # S型GTO基函数,4个原函数收缩成2个
3.836000E+01 # 4个S型高斯原函数的指数
5.770000E+00
1.240000E+00
2.976000E-01
2.380900E-02 0.000000E+00 # 两列收缩因子,对应两个收缩的S型GTO基函数
1.548910E-01 0.000000E+00
4.699870E-01 0.000000E+00
5.130270E-01 1.000000E+00
P 2 2 # P型GTO基函数,2个原函数收缩成2个
1.275000E+00
4.000000E-01
1.0000000E+00 0.000000E+00
0.0000000E+00 1.000000E+00
**** # 4个星号结束He的基组,后面可接另一个元素的基组,或者结束
Al 13 2
(略)
在以上的基组中,P函数未作收缩,也可以写成以下形式:
(S函数,略)
P 2 0 # 0表示非收缩,此时不需要提供收缩因子
1.275000E+00
4.000000E-01
****
(略)
对于赝势基组,还需要在价基函数后提供ECP数据。例如,
**** # 价基函数部分,注释同上
Al 13 2
S 4 3
14.68000000
0.86780000
0.19280000
0.06716000
-0.0022368000 0.0000000000 0.0000000000
-0.2615913000 0.0000000000 0.0000000000
0.6106597000 0.0000000000 1.0000000000
0.5651997000 1.0000000000 0.0000000000
P 4 2
6.00100000
1.99200000
0.19480000
0.05655000
-0.0034030000 0.0000000000
-0.0192089000 0.0000000000
0.4925534000 -0.2130858000
0.6144261000 1.0000000000
D 1 1
0.19330000
1.0000000000
ECP # 价基函数之后立即接关键词ECP(全部大写),表示后面是ECP数据部分
Al 10 2 2 # 相同的元素符号,芯电子数,ECP最高角动量,可选的SOECP最高角动量
D potential 4 # ECP最高角动量(D函数)的势函数个数
2 1.22110000000000 -0.53798100000000 # R的幂,指数,因子(下同)
2 3.36810000000000 -5.45975600000000
2 9.75000000000000 -16.65534300000000
1 29.26930000000000 -6.47521500000000
S potential 5 # S投影的个数
2 1.56310000000000 -56.20521300000000
2 1.77120000000000 149.68995500000000
2 2.06230000000000 -91.45439399999999
1 3.35830000000000 3.72894900000000
0 2.13000000000000 3.03799400000000
P potential 5 # P投影的个数
2 1.82310000000000 93.67560600000000
2 2.12490000000000 -189.88896800000001
2 2.57050000000000 110.24810400000000
1 1.75750000000000 4.19959600000000
0 6.76930000000000 5.00335600000000
P so-potential 5 # P-SO投影的个数,标量ECP没有这一部分
2 1.82310000000000 1.51243200000000 # 标量ECP没有这一部分
2 2.12490000000000 -2.94701800000000 # 标量ECP没有这一部分
2 2.57050000000000 1.64525200000000 # 标量ECP没有这一部分
1 1.75750000000000 -0.08862800000000 # 标量ECP没有这一部分
0 6.76930000000000 0.00681600000000 # 标量ECP没有这一部分
D so-potential 4 # D-SO投影的个数,标量ECP没有这一部分
2 1.22110000000000 -0.00138900000000 # 标量ECP没有这一部分
2 3.36810000000000 0.00213300000000 # 标量ECP没有这一部分
2 9.75000000000000 0.00397700000000 # 标量ECP没有这一部分
1 29.26930000000000 0.03253000000000 # 标量ECP没有这一部分
****
对于标量ECP,SOECP最高角动量为0(可以省略不写),不需要提供SO投影部分的数据。
把以上数据保存后,就可以在BDF输入文件中调用 MYBAS-1 基组,这需要通过以下的混合输入模式实现:
#!bdfbasis.sh
HF/genbas
Geometry
.....
End geometry
$Compass
Basis
mybas-1 # 给出当前目录下基组文件的名字,这里不区分大小写
$End
自定义基组必须用BDF的混合模式输入。在第二行输入基组设置为 genbas , 自定义基组文件名需要在 COMPASS 模块使用关键词 Basis ,值为 mybas-1 ,表示调用名为 MYBAS-1 的基组文件。
基组的指定
对所有原子使用相同的BDF内置基组
简洁输入模式,基组在 方法/泛函/基组 或者 方法/基组 中指定。这里 基组 是前几节所列的BDF内置的基组名称,输入字符大小写不敏感,如下所示:
#! basisexample.sh
TDDFT/PBE0/3-21g
Geometry
H 0.000 0.000 0.000
Cl 0.000 0.000 1.400
End geometry
#! basisexample.sh
HF/lanl2dz
Geometry
H 0.000 0.000 0.000
Cl 0.000 0.000 1.400
End geometry
如果是高级输入模式,计算采用的基组在 compass 模块中利用关键词 basis 指定,例如
$compass
Basis
lanl2dz
Geometry
H 0.000 0.000 0.000
Cl 0.000 0.000 1.400
End geometry
$end
其中 lanl2dz 调用内置的LanL2DZ基组(已在 basisname 文件中注册),不区分大小写。
为不同元素指定不同基组
简洁输入不支持自定义或者混合基组,必须采用混合输入模式,即在 方法/泛函/基组 中设置 基组 为 genbas , 并添加 COMPASS 模块输入,使用 basis-block … end basis 关键词指定基组。
如果对不同元素指定不同名称的基组,需要放在 COMPASS 模块的 basis-block … end basis 块中,
其中第一行是默认基组,之后的行对不同元素指定其它基组,格式为 元素=基组名 或者 元素1,元素2, …,元素n=基组名 。
例如,混合输入模式下,对不同原子使用不同基组的示例如下:
#! multibasis.sh
HF/genbas
Geometry
H 0.000 0.000 0.000
Cl 0.000 0.000 1.400
End geometry
$compass
Basis-block
lanl2dz
H = 3-21g
End Basis
$end
上例中,H使用3-21G基组,而未额外定义的Cl采用默认的LanL2DZ基组。
如果是高级输入,如下:
$compass
Basis-block
lanl2dz
H = 3-21g
End Basis
Geometry
H 0.000 0.000 0.000
Cl 0.000 0.000 1.400
End geometry
$end
为同种元素的不同原子指定不同基组
BDF也可以为同一元素中的不同原子指定不同名称的基组,这些原子需要在元素符号后加上任意的数字以示区分。例如,
#! CH4.sh
RKS/B3lyp/genbas
Geometry
C 0.000 -0.000 0.000
H1 -0.000 -1.009 -0.357
H2 -0.874 0.504 -0.457
H1 0.874 0.504 -0.357
H2 0.000 0.000 1.200
End geometry
$compass
Basis-block
6-31g
H1= cc-pvdz
H2= 3-21g
End basis
$end
上例中,H1类型的两个氢原子用cc-pVDZ基组,H2类型的两个氢原子用3-21G基组,碳原子用6-31G基组。需要注意的是,对称等价原子必须使用相同基组,程序将对此进行检查;
如果对称等价原子必须要使用不同基组,可通过 Group 设置较低的点群对称性,或者用 Nosymm 关闭对称性。
辅助基组
使用密度拟合近似(RI)的方法需要一个辅助的基组。Ahlrichs系列基组和Dunning相关一致性基组以及其它个别基组有专门优化的辅助基组。BDF中可以在compass中通过 RI-J、 RI-K 和 RI-C 关键词指定辅助基组。其中 RI-J 用于指定库伦拟合基组, RI-K 用于指定库伦交换拟合基组, RI-C 用于指定库伦相关拟合基组。BDF支持的辅助基组保存在 $BDFHOME/basis_library 路径下对应的文件夹中。
高级别密度拟合基组可以用在低级别基组上,例如 cc-pVTZ/C 可以用于在 cc-pVTZ 上做RI-J,对于没有标配辅助基组的pople系列基组如 6-31G** 也可以用 cc-pVTZ/J 做RI-J或RIJCOSX。反之,高级别轨道基组结合低级别的辅助基组则会带来较明显的误差。
$Compass
Basis
DEF2-SVP
RI-J
DEF2-SVP
Geometry
C 1.08411 -0.01146 0.05286
H 2.17631 -0.01146 0.05286
H 0.72005 -0.93609 0.50609
H 0.72004 0.05834 -0.97451
H 0.72004 0.84336 0.62699
End Geometry
$End
上例中,使用 def2-SVP 基组计算 \(\ce{CH4}\) 甲烷分子,同时用def2-SVP标配的库伦拟合基组进行加速计算。
提示
BDF的RI计算功能,用于加速 MCSCF、 MP2 等波函数计算方法,不推荐用户在 SCF 、 TDDFT 等计算中使用,用户可以用多级展开库伦势 (MPEC) 方法,MPEC方法不依赖辅助基组,计算速度和精度都与RI方法相当。
BDF支持的交换相关泛函
BDF的密度泛函理论(DFT)支持限制性(restricted)、非限制性(unrestricted)和 限制性开壳层(restricted open-shell)Kohn-Sham计算,分别简称为RKS,UKS和ROKS。其输入与RHF、UHF和ROHF接近, 关键是要指定交换相关泛函。BDF支持LDA,GGA,Meta-GGA,Hybrid,RS Hybrid和Hybrid Meta-GGA等多种泛函。
泛函类型 |
泛函 |
|---|---|
局域密度近似(LDA) |
LSDA, SVWN5, SAOP |
广义梯度近似(GGA) |
BP86, BLYP, PBE, PW91, OLYP, KT2 |
含动能密度的广义梯度近似(meta-GGA) |
TPSS, M06L, M11L, MN12L, MN15L, SCAN, r2SCAN |
杂化GGA泛函(Hybrid GGA) |
B3LYP, GB3LYP, BHHLYP, PBE0, B3PW91, HFLYP, VBLYP |
范围分离GGA泛函(RS Hybrid GGA) |
wB97, wB97X, wB97X-D,CAM-B3LYP, LC-BLYP |
杂化含动能密度泛函(Hybrid Meta-GGA) |
TPSSh, M062X, PW6B95 |
双杂化泛函(Double Hybrid) |
B2PLYP |
注意
B3LYP的LDA相关项采用VWN5, 而GB3LYP对应Gaussian程序中的B3LYP,LDA相关项采用VWN3。
如果是非积分直接的SCF计算,对于范围分离泛函,必须手动在
Xuanyuan模块里设定rs值(参见 xuanyuan模块的关键词列表 )。wB97, wB97X, wB97X-D, CAM-B3LYP, LC-BLYP的rs值分别为0.40, 0.30, 0.20, 0.33和0.33。对于双杂化泛函计算,必须在
SCF模块后面添加一个MP2模块(参见 算例说明 里的算例test116),并从MP2模块的输出读取最终结果。可以在
SCF模块里用facex和facco关键字调整泛函的HF交换项比例和MP2相关项比例,从而实现用户自定义泛函(参见 SCF模块的关键词列表 )。BDF使用了libxc,原则上支持libxc所包含的所有泛函,但需要时间来完善与补充。用户可以向我们反馈需要的泛函,以便我们按照需求来补充。
需要注意的是,虽然所有泛函都支持(不带色散校正的)基态单点能计算,但是有的功能只被部分泛函支持。以下是各种计算任务支持的泛函列表:
计算任务类型 |
泛函 |
|---|---|
TDDFT单点能、SOC计算 |
除双杂化泛函外的所有泛函 |
TDDFT激发态偶极矩 |
LSDA, SVWN5, BP86, BLYP, PBE, OLYP, B3LYP, GB3LYP, BHHLYP, PBE0, HFLYP, CAM-B3LYP, LC-BLYP |
基态梯度 |
除SAOP、PW91、KT2、B3PW91、VBLYP、SF5050外的所有LDA、GGA、杂化GGA泛函、meta-GGA和杂化meta-GGA泛函 |
激发态梯度、NAC |
除SAOP、PW91、KT2、B3PW91、VBLYP、SF5050外的所有LDA、GGA和杂化GGA泛函 |
能量转移/电子转移积分 |
所有泛函均支持,但其中B2PLYP的结果不包含MP2相关项的贡献,因而是近似的 |
NMR |
所有的LDA、GGA和杂化GGA泛函 |
色散校正 |
BP86, BLYP, PBE, B3LYP, GB3LYP, BHHLYP, B3PW91, PBE0, CAM-B3LYP, B2PLYP, wB97X-D |
自洽场方法:Hartree-Fock和Kohn-Sham
BDF的自洽场包括Hartree-Fock和Kohn-Sham方法。
限制性Hartree-Fock方法
限制性Hatree-Fock方法(RHF)的示例已在 第一个算例一节 提及,这里不再赘述。
非限制性Hartree-Fock方法
对于有不成对电子的体系,需要用 UHF 方法,此外也可以用限制性开壳层Hartree-Fock (restricted open-shell Hartree-Fock)方法,见后。
对于奇数电子体系,BDF默认自旋多重度为2,且利用UHF计算。例如计算 \(\ce{C3H5}\) 分子,
#!bdf.sh
UHF/3-21G
geometry
C 0.00000000 0.00000000 0.00000000
C 0.00000000 0.00000000 1.45400000
C 1.43191047 0.00000000 1.20151555
H 0.73667537 -0.61814403 -0.54629970
H -0.90366611 0.32890757 -0.54629970
H 2.02151364 0.91459433 1.39930664
H 2.02151364 -0.91459433 1.39930664
H -0.79835551 0.09653770 2.15071009
end geometry
UHF计算输出和RHF类似,从 scf 模块输出可以检查电荷和自旋多重度是否正确,
Wave function information ...
Total Nuclear charge : 23
Total electrons : 23
Ecp-core electrons : 0
Spin multiplicity(2S+1) : 2
Num. of alpha electrons : 12
Num. of beta electrons : 11
轨道占据情况按 Alpha 和 Beta 轨道分别给出,
[Final occupation pattern: ]
Irreps: A
detailed occupation for iden/irep: 1 1
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
1.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
Alpha 12.00
detailed occupation for iden/irep: 2 1
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
Beta 11.00
轨道能, HOMO-LUMO gap 也按照 Alpha 和 Beta 轨道分开打印
[Orbital energies:]
Energy of occ-orbsA: A 12
-11.18817955 -11.18789391 -11.17752809 -1.11801069 -0.85914580
-0.78861789 -0.65514687 -0.61300160 -0.55514631 -0.49906127
-0.37655522 -0.30477047
Energy of vir-orbsA: A 25
0.18221017 0.28830234 0.31069644 0.32818004 0.35397043
0.38822931 0.42917813 0.49394022 0.93909970 0.94842069
0.96877856 0.97277131 1.02563249 1.05399606 1.11320732
1.17687697 1.26547430 1.31245896 1.32719078 1.34493766
1.37905664 1.45903968 1.80285556 1.93877012 2.01720415
Energy of occ-orbsB: A 11
-11.19670896 -11.16769083 -11.16660825 -1.07470168 -0.84162305
-0.74622771 -0.63695581 -0.58068095 -0.53876236 -0.46400924
-0.37745766
Energy of vir-orbsB: A 26
0.15755278 0.18938428 0.30608423 0.33204779 0.33996597
0.38195612 0.39002159 0.43644421 0.52237314 0.94876233
0.96144960 0.97568581 1.01804430 1.05467405 1.09547593
1.13390456 1.19865205 1.28139866 1.32654541 1.33938005
1.34914150 1.38200544 1.47565481 1.79509704 1.96917149
2.03513467
Alpha HOMO energy: -0.30477047 au -8.29322996 eV Irrep: A
Alpha LUMO energy: 0.18221017 au 4.95819299 eV Irrep: A
Beta HOMO energy: -0.37745766 au -10.27114977 eV Irrep: A
Beta LUMO energy: 0.15755278 au 4.28723115 eV Irrep: A
HOMO-LUMO gap: 0.46232325 au 12.58046111 eV
其他输出信息可参见RHF计算的例子,这里不再冗述。值得一提的是,与RHF计算不同,UHF计算不仅会打印原子电荷,还会同时打印原子的自旋布居数:
[Mulliken Population Analysis]
Atomic charges and Spin densities :
1C -0.4197 -1.0689
2C -0.3255 1.0138
3C -0.3633 0.9077
4H 0.2548 0.1237
5H 0.2039 0.1504
6H 0.2038 -0.0404
7H 0.2012 -0.0207
8H 0.2447 -0.0657
Sum: -0.0000 1.0000
[Lowdin Population Analysis]
Atomic charges and Spin densities :
1C -0.1790 -0.8011
2C -0.1431 0.8584
3C -0.1804 0.8007
4H 0.1194 0.0909
5H 0.0840 0.0982
6H 0.0894 -0.0126
7H 0.0886 0.0006
8H 0.1212 -0.0352
Sum: 0.0000 1.0000
例如以上输出表示,1号C原子上有约1个自旋向下的单电子,而2、3号碳原子上各有约1个自旋向上的单电子。
限制性开壳层Hartree-Fock方法
限制性开壳层Hartree-Fock(Restricted open-shell Hartree-Fock - ROHF)也可以计算开壳层分子体系。这里给出一个 \(\ce{CH2}\) 三重态的ROHF算例,
#!bdf.sh
rohf/cc-pvdz spinmulti=3
geometry # 输入坐标单位 Angstrom
C 0.000000 0.00000 0.31399
H 0.000000 -1.65723 -0.94197
H 0.000000 1.65723 -0.94197
end geometry
这里,在第二行指定使用 ROHF 方法,且利用关键词 spinmulti=3 设定计算三重态。ROHF的输出和UHF类似,
但其 Alpha 轨道和 Beta 是一样的,所以相对应的 Alpha 和 Beta 轨道能量相等,如下所示:
[Orbital energies:]
Energy of occ-orbsA: A1 3
-11.42199273 -0.75328533 -0.22649749
Energy of vir-orbsA: A1 8
0.05571960 0.61748052 0.70770696 0.83653819 1.29429307
1.34522491 1.56472153 1.87720054
Energy of vir-orbsA: A2 2
1.34320056 1.53663810
Energy of occ-orbsA: B1 1
-0.37032603
Energy of vir-orbsA: B1 6
0.06082087 0.66761691 0.77091474 1.23122892 1.51131609
1.91351353
Energy of occ-orbsA: B2 1
-0.16343739
Energy of vir-orbsA: B2 3
0.65138659 1.35768658 1.54657952
Energy of occ-orbsB: A1 2
-11.42199273 -0.75328533
Energy of vir-orbsB: A1 9
-0.22649749 0.05571960 0.61748052 0.70770696 0.83653819
1.29429307 1.34522491 1.56472153 1.87720054
Energy of vir-orbsB: A2 2
1.34320056 1.53663810
Energy of occ-orbsB: B1 1
-0.37032603
Energy of vir-orbsB: B1 6
0.06082087 0.66761691 0.77091474 1.23122892 1.51131609
1.91351353
Energy of vir-orbsB: B2 4
-0.16343739 0.65138659 1.35768658 1.54657952
由于 Alpha 与 Beta 轨道的占据数不同, Alpha 的HOMO、LUMO轨道、轨道能与 Beta 的不同,如下:
Alpha HOMO energy: -0.16343739 au -4.44735961 eV Irrep: B2
Alpha LUMO energy: 0.05571960 au 1.51620803 eV Irrep: A1
Beta HOMO energy: -0.37032603 au -10.07708826 eV Irrep: B1
Beta LUMO energy: -0.22649749 au -6.16331290 eV Irrep: A1
HOMO-LUMO gap: -0.06306010 au -1.71595329 eV
RKS,UKS,和ROKS计算
对于限制性Kohn-Sham(Restricted Kohn-Sham, RKS)方法,这里以简洁输入的模式给出一个 \(\ce{H2O}\) 分子的RKS计算算例,使用了B3lyp泛函。
#!bdf.sh
B3lyp/3-21G
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length, unit is Angstrom
end geometry
这个输入对应的高级模式的输入为
$compass
geometry # On default: bond length unit in angstrom
o
h 1 1.0
h 1 1.0 2 109.
end geometry
basis
3-21g
$end
$xuanyuan
$end
$scf
rks # Restricted Kohn-Sham calculation
dft # ask for B3lyp functional, it is different with B3lyp implemented in Gaussian.
b3lyp
$end
这里,输入要求使用 B3lyp 泛函。相比于Hartree-Fock,输出多了Exc项的贡献,如下所示:
Final scf result
E_tot = -75.93603354
E_ele = -84.72787022
E_nn = 8.79183668
E_1e = -122.04354727
E_ne = -197.45852687
E_kin = 75.41497960
E_ee = 44.81744844
E_xc = -7.50177140
Virial Theorem 2.006909
\(\ce{H2O+}\) 离子的ROKS计算,简洁输入如下,
#!bdf.sh
ROKS/B3lyp/cc-pvdz charge=1
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
提示
相比于Hartree-Fock,Kohn-Sham需要在高级输入使用dft关键词指定交换相关泛函。如果是简洁输入,只需指定交换相关泛函和基组。系统会根据自旋态选择使用RKS或UKS,如果要使用ROKS,必须明确输入。
基于RS杂化泛函的Kohn-Sham计算
CAM-B3LYP等RS杂化泛函,将库伦相互作用分为长短程,
采用BDF高级输入时,可以通过xuanyuan模块中的关键词RS,调整 \(\mu\) 参数。CAM-B3lyp默认的 \(\mu\) 参数为0.33, 其它范围分离泛函中的 \(\mu\) 值见 RSOMEGA 关键词。 例如 1,3-Butadiene 分子,利用CAM-B3lyp的RKS高级模式输入为,
$compass
basis
cc-pVDZ
geometry
C -2.18046929 0.68443844 -0.00725330
H -1.64640852 -0.24200621 -0.04439369
H -3.24917614 0.68416040 0.04533562
C -1.50331750 1.85817167 -0.02681816
H -0.43461068 1.85844971 -0.07940766
C -2.27196552 3.19155924 0.02664018
H -3.34067218 3.19128116 0.07923299
C -1.59481380 4.36529249 0.00707382
H -2.12887455 5.29173712 0.04421474
H -0.52610710 4.36557056 -0.04551805
end geometry
$end
$xuanyuan
rs
0.33 # define mu=0.33 in CAM-B3lyp functional
$end
$scf
rks # restricted Kohn-Sham
dft
cam-b3lyp
$end
自定义杂化泛函、双杂化泛函的精确交换项和相关项成分
对于某些计算,可能需要用户手动调节泛函的精确交换项成分,才能获得满意的精度。此时可在 $scf 模块里加入 facex 关键词,例如若要将B3LYP泛函的精确交换项成分由默认的20%改为15%,可以写
$scf
...
dft
b3lyp
facex
0.15
$end
类似地,可以用 facco 关键词自定义双杂化泛函的MP2相关项成分。注意并不是所有泛函都支持自定义facex和facco(参见 SCF模块的关键词列表 )。
对弱相互作用的色散矫正
常见的交换相关泛函如B3lyp不能很好地描述弱相互作用,需要在计算能量或者做分子结构优化时,加入色散矫正。BDF采用了Stefan Grimme开发的 D3色散矫正方法,需要在SCF模块的输入中指定D3关键词,输入如下,
#!bdf.sh
B3lyp/cc-pvdz
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
$scf
D3 # Grimme's dispersion correction
$end
小技巧
这里使用了BDF混合模式的输入方式,在简洁输入基础上,通过添加SCF模块关键词精确控制SCF计算。
在Kohn-Sham计算结束后加入色散矫正,计算输出如下,
diis/vshift is closed at iter = 8
9 0 0.000 -76.380491166 -0.000000000 0.000000017 0.000000168 0.0000 0.02
Label CPU Time SYS Time Wall Time
SCF iteration time: 0.467 S 0.033 S 0.233 S
Final DeltaE = -7.5459638537722640E-011
Final DeltaD = 1.6950036756030376E-008 5.0000000000000002E-005
Final scf result
E_tot = -76.38106481
E_ele = -85.17290149
E_disp= -0.00057364
E_nn = 8.79183668
E_1e = -122.51287853
E_ne = -198.42779201
E_kin = 75.91491348
E_ee = 44.84995532
E_xc = -7.50940464
Virial Theorem 2.006140
这里的总能量 E_tot 包含了色散矫正能, E_disp = -0.00057364 。
提高Kohn-Sham计算的积分格点精度
虽然BDF对不同的泛函按照精度要求定义了默认积分格点(例如Meta-GGA类泛函对积分格点要求很高,BDF默认使用Fine格点),
用户可能还希望对积分格点进行调节。Kohn-Sham泛函的积分格点可以在SCF模块的输入中通过Grid关键词定义,Grid的有效值为 Ultra coarse ,
Coarse , medium , fine , Ultra fine 等5个,从 Ultra coarse 到 Ultra fine 积分格点依次增加,数值积分精度依次提高。
示例: \(\ce{H2O}\) 分子的M062X计算。该泛函属于杂化Meta-GGA类型泛函,要求密集的积分格点,因此输入用到了高级输入和简洁输入混合模式,如下所示:
#!bdf.sh
M062X/cc-pvdz
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
$scf
grid # set numerical integration grid as ultra fine
ultra fine
$end
BDF在Kohn-Sham计算的开始几步采用 Ultra coarse 积分格点,如下所示,
Switch to Ultra Coarse grid ...
[ATOM SCF control]
heff= 0
After initial atom grid ...
After initial atom grid ...
Generating Numerical Integration Grid.
1 O Second Kind Chebyshev ( 21) Lebedev ( -194)
Atoms: 1
2 H Second Kind Chebyshev ( 21) Lebedev ( -194)
Atoms: 2 3
Partition Function: SSF Partitioning with Scalar= 0.64.
Gtol, Npblock, Icoulpot, Iop_adaptive : 0.10E-04 128 0 0
Number of symmetry operation = 4
Basis Informations for Self-adaptive Grid Generation, Cutoff= 0.10E-04
1O GTO( 14) Ntot= 26 MaxL= 2 MaxNL= 0 MaxRad= 0.530E+01
basis details in form ( N L Zeta Cutradius):
( 1 0 0.117E+05 0.02) ( 1 0 0.176E+04 0.06) ( 1 0 0.401E+03 0.13)
( 1 0 0.114E+03 0.24) ( 1 0 0.370E+02 0.42) ( 1 0 0.133E+02 0.70)
( 1 0 0.503E+01 1.14) ( 1 0 0.101E+01 2.53) ( 1 0 0.302E+00 4.64)
( 2 1 0.177E+02 0.66) ( 2 1 0.385E+01 1.42) ( 2 1 0.105E+01 2.72)
( 2 1 0.275E+00 5.30) ( 3 2 0.119E+01 2.73)
2H GTO( 5) Ntot= 7 MaxL= 1 MaxNL= 0 MaxRad= 0.730E+01
basis details in form ( N L Zeta Cutradius):
( 1 0 0.130E+02 0.71) ( 1 0 0.196E+01 1.82) ( 1 0 0.445E+00 3.82)
( 1 0 0.122E+00 7.30) ( 2 1 0.727E+00 3.26)
Numerical Grid Generated SUCCESSFULLY!
Total and symmetry independent Grid Number: 4352 1181
当能量收敛到0.01 Hartree之内时,会切换到 Ultra fine 积分格点,输出如下所示:
Switch to Ultra Fine grid ...
[ATOM SCF control]
heff= 0
After initial atom grid ...
After initial atom grid ...
Generating Numerical Integration Grid.
1 O Second Kind Chebyshev (100) Lebedev (-1202)
Atoms: 1
2 H Second Kind Chebyshev (100) Lebedev (-1202)
Atoms: 2 3
Partition Function: SSF Partitioning with Scalar= 0.64.
Gtol, Npblock, Icoulpot, Iop_adaptive : 0.10E-04 128 0 0
Number of symmetry operation = 4
Basis Informations for Self-adaptive Grid Generation, Cutoff= 0.10E-04
1O GTO( 14) Ntot= 26 MaxL= 2 MaxNL= 0 MaxRad= 0.530E+01
basis details in form ( N L Zeta Cutradius):
( 1 0 0.117E+05 0.02) ( 1 0 0.176E+04 0.06) ( 1 0 0.401E+03 0.13)
( 1 0 0.114E+03 0.24) ( 1 0 0.370E+02 0.42) ( 1 0 0.133E+02 0.70)
( 1 0 0.503E+01 1.14) ( 1 0 0.101E+01 2.53) ( 1 0 0.302E+00 4.64)
( 2 1 0.177E+02 0.66) ( 2 1 0.385E+01 1.42) ( 2 1 0.105E+01 2.72)
( 2 1 0.275E+00 5.30) ( 3 2 0.119E+01 2.73)
2H GTO( 5) Ntot= 7 MaxL= 1 MaxNL= 0 MaxRad= 0.730E+01
basis details in form ( N L Zeta Cutradius):
( 1 0 0.130E+02 0.71) ( 1 0 0.196E+01 1.82) ( 1 0 0.445E+00 3.82)
( 1 0 0.122E+00 7.30) ( 2 1 0.727E+00 3.26)
Numerical Grid Generated SUCCESSFULLY!
Total and symmetry independent Grid Number: 94208 24827
这里,H和O原子的积分格点都为100*1202,其中,100是径向格点的数目,1202是角向格点的数目。
对称性与分子点群
BDF支持在计算中考虑分子点群对称性。除某些计算任务(如开壳层TDDFT、TDDFT/SOC等)仅支持 \(\rm D_{2h}\) 及其子群(即 \(\rm C_1, C_i, C_s, C_2, D_2, C_{2h}, C_{2v}, D_{2h}\) ,一般统称为阿贝尔群)以外,大部分计算任务支持任何的实表示点群(所有的阿贝尔群,以及 \(\rm C_{nv}, D_{n}, D_{nh}, D_{nd}, T_d, O, O_h, I, I_h\) ;其中特殊点群 \(\rm C_{\infty v}, D_{\infty h}\) 虽然名义上支持,但是是分别当作 \(\rm C_{20v}\) 和 \(\rm D_{20h}\) 来处理的,而单个原子按 \(\rm O_{h}\) 群处理),但不支持复表示点群( \(\rm C_n, C_{nh} (n \ge 3); S_{2n} (n \ge 2); T, T_h\) )。程序可以自动根据用户在COMPASS模块输入的分子坐标来判断分子所属的点群,并在分子属于复表示点群时自动改用合适的子群。确定分子所属点群以后,程序即可产生该点群的群操作算符、特征标表、不可约表示等信息,以备后续计算使用。以氨分子为例:
#! NH3.sh
HF/cc-pVDZ
geometry
N -0.00000000 -0.00000000 -0.10000001
H 0.00000000 -0.94280900 0.23333324
H -0.81649655 0.47140450 0.23333324
H 0.81649655 0.47140450 0.23333324
end geometry
$compass
Title
NH3
thresh
medium
$end
对应的高级输入模式,COMPASS 中的内容为
$COMPASS
Title
NH3
Basis
cc-pvdz
Geometry
N -0.00000000 -0.00000000 -0.10000001
H 0.00000000 -0.94280900 0.23333324
H -0.81649655 0.47140450 0.23333324
H 0.81649655 0.47140450 0.23333324
End geometry
thresh
medium
$END
注意因为初始结构不严格满足 \(\rm C_{3v}\) 对称性,这里用 thresh medium 选择较松的判断对称性的阈值(默认为 tight ,也可选择更松的 loose )。由输出文件可以看到,程序自动识别出该分子属于 \(\rm C_{3v}\) 点群:
gsym: C03V, noper= 6
Exiting zgeomsort....
Representation generated
Point group name C(3V) 6
User set point group as C(3V)
Largest Abelian Subgroup C(S) 2
注意点群名称的下标需要用括号括起来,诸如 \(\rm C_{\infty v}, D_{\infty h}\) 群需要写作C(LIN)、D(LIN)。接下来打印不可约表示信息、CG系数表等。在COMPASS部分输出的最后,程序给出该点群下不可约表示的列表,以及属于每个不可约表示的轨道的数目:
|--------------------------------------------------|
Symmetry adapted orbital
Total number of basis functions: 29 29
Number of irreps: 3
Irrep : A1 A2 E1
Norb : 10 1 18
|--------------------------------------------------|
不可约表示的排列顺序
很多时候,用户需要在输入文件中指定诸如每个不可约表示的轨道占据数(在SCF模块的输入中指定),以及每个不可约表示下计算多少个激发态(在TDDFT模块的输入中指定)等信息,而这些信息一般是以数组的形式提供的,例如
$TDDFT
Nroot
3 1 2
$END
表示第一个不可约表示计算3个激发态,第二个不可约表示计算1个激发态,第三个不可约表示计算2个激发态(详见本手册的 TDDFT章节)。这就势必要求用户在撰写输入文件时已知道各个不可约表示在BDF程序内部的排列顺序。以下给出BDF支持的所有点群下各个不可约表示的排列顺序:
C(1) |
A |
C(i) |
Ag, Au |
C(s) |
A’, A” |
C(2) |
A, B |
C(2v) |
A1, A2, B1, B2 |
C(2h) |
Ag, Bg, Au, Bu |
D(2) |
A, B1, B3, B2 (注:在2023.3.12及以后发布的版本中,排列顺序变为A, B1, B2, B3) |
D(2h) |
Ag, B1g, B3g, B2g, Au, B1u, B3u, B2u (注:在2023.3.12及以后发布的版本中,排列顺序变为Ag, B1g, B2g, B3g, Au, B1u, B2u, B3u) |
C(nv) (n=2k+1, k>=1) |
A1, A2, E1, …, Ek |
C(nv) (n=2k+2, k>=1) |
A1, A2, B1, B2, E1, …, Ek |
D(n) (n=2k+1, k>=1) |
A1, A2, E1, …, Ek |
D(n) (n=2k+2, k>=1) |
A1, A2, B1, B2, E1, …, Ek |
D(nh) (n=2k+1, k>=1) |
A1’, A2’, E1’, …, Ek’, A1”, A2”, E1”, …, Ek”, |
D(nh) (n=2k+2, k>=1) |
A1g, A2g, B1g, B2g, E1g, …, Ekg, A1u, A2u, B1u, B2u, E1u, …, Eku |
D(nd) (n=2k+1, k>=1) |
A1g, A2g, E1g, …, Ekg, A1u, A2u, E1u, …, Eku |
D(nd) (n=2k+2, k>=1) |
A1’, A2’, B1’, B2’, E1’, …, Ek’, A1”, A2”, B1”, B2”, E1”, …, Ek” |
T(d) |
A1, A2, E, T1, T2 |
O |
A1, A2, E, T1, T2 |
O(h) |
A1g, A2g, Eg, T1g, T2g, A1u, A2u, Eu, T1u, T2u |
I |
A, T1, T2, F, H |
I(h) |
Ag, T1g, T2g, Fg, Hg, Au, T1u, T2u, Fu, Hu |
用户也可强制程序在分子所属点群的某个子群下计算,方法是在COMPASS模块的输入里使用group关键词,如:
#! N2.sh
HF/def2-TZVP group=D(2h)
geometry
N 0.00 0.00 0.00
N 0.00 0.00 1.10
end geometry
或者
$COMPASS
Title
N2
Basis
def2-TZVP
Geometry
N 0.00 0.00 0.00
N 0.00 0.00 1.10
End geometry
Group
D(2h)
$END
即强制程序在 \(\rm D_{2h}\) 点群下计算 \(\rm N_2\) 分子,尽管 \(\rm N_2\) 分子实际上属于 \(\rm D_{\infty h}\) 点群。注意程序会自动检查用户输入的点群是否是分子实际所属点群的子群;如否,则程序报错退出。
标准取向 (standard orientation)
为了计算以及结果分析方便起见,程序在确定计算所用点群以后,会将分子旋转到标准取向,以使得分子的对称轴尽量和坐标轴重合,对称面尽量和坐标轴垂直。这样的好处在于可以让计算涉及的很多量精确等于0(如某些分子轨道系数,梯度的某些分量等),方便分析计算结果。
BDF按照以下规则确定分子的标准取向:
将分子的所有原子坐标按核电荷取加权平均,得到分子的核电荷中心,然后平移分子使得核电荷中心位于坐标系原点;
如果分子有对称轴,将分子的最高阶对称轴(主轴)旋转至z轴方向;
如果分子有 \(\sigma_v\) 对称面,将其中一个 \(\sigma_v\) 对称面旋转至xz平面方向,过程中保证主轴方向不变;
如果分子除主轴外还有其他的二重轴或四重轴,将其中一根轴(如果存在四重轴,则选择任意一根四重轴,否则选择任意一根二重轴)旋转至x轴方向,过程中保证主轴方向不变;
如果因为分子的对称性太低,以上各条件不能唯一确定分子的取向,则旋转分子使得分子的惯性轴(即转动惯量的本征矢)和各坐标轴方向一致。
对于某些特殊情形,以上规则仍无法唯一确定分子的取向。例如属于 \(\rm C_{2v}\) 、 \(\rm D_{2h}\) 点群的分子,因有两个 \(\sigma_v\) 对称面,在上述规则的第3步时任一个对称面均有可能被旋转到xz方向。在BDF里,如水分子等平面结构的 \(\rm C_{2v}\) 分子会被旋转到xz平面:
|-----------------------------------------------------------------------------------|
Atom Cartcoord(Bohr) Charge Basis Auxbas Uatom Nstab Alink Mass
O 0.000000 -0.000000 0.219474 8.00 1 0 0 0 E 15.9949
H -1.538455 0.000000 -0.877896 1.00 2 0 0 0 E 1.0073
H 1.538455 -0.000000 -0.877896 1.00 2 0 0 0 E 1.0073
|------------------------------------------------------------------------------------|
相比之下其他量化程序则可能选择将分子旋转至yz平面。由此会带来另一个问题:根据习惯约定, \(\rm C_{2v}\) 点群下 \(\mathbf{x}\) 算符属于B1不可约表示, \(\mathbf{y}\) 算符属于B2不可约表示,因此如果某量化程序选择将分子转至yz平面,则其B1、B2不可约表示的定义和BDF是相反的,即该程序的B1表示对应于BDF的B2表示,该程序的B2表示对应于BDF的B1表示。而如果该 \(\rm C_{2v}\) 点群的分子不是平面结构(如环氧乙烷),则更加难以预测BDF中分子的标准取向是否和其他量化软件一致。因此如果用户希望计算 \(\rm C_{2v}\) 、 \(\rm D_{2h}\) 点群的分子,并与其他量化程序的结果相比较(或者试图重复文献用其他量化程序计算出来的结果),则用户必须确认该量化程序的B1、B2表示是如何和BDF对应的。
自洽场计算的其它技巧
自洽场计算的初始猜测
自洽场计算的初始猜测轨道,对计算的收敛性有很大的影响。BDF支持多种初始猜测,如下所示:
Atom : 利用原子密度矩阵组合分子密度矩阵猜测,默认选项。
Huckel : 半经验Huckel方法猜测;
Hcore : 对角化单电子哈密顿猜测;
Readmo : 读入分子轨道做为初始猜测;
BDF默认用Atom猜测。在简洁输入模式下可以使用关键词 guess 改变BDF的初始猜测,如下所示
#! ch3cho.sh
HF/6-31G guess=Hcore unit=Bohr
geometry # notice: unit in Bohr
C 0.1727682300 -0.0000045651 -0.8301598059
C -2.3763311896 0.0000001634 0.5600567139
H 0.0151760290 0.0000088544 -2.9110013387
H -2.0873396672 0.0000037621 2.5902220967
H -3.4601725077 -1.6628370597 0.0320271859
H -3.4601679801 1.6628382651 0.0320205364
O 2.2198078005 0.0000024315 0.2188182082
end geometry
这里,我们在第二行是用了关键词 guess=Hcore 指定使用 Hcore 猜测。SCF迭代了18次收敛。
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -130.488739529 174.680929376 0.401531162 5.325668770 0.0000 0.03
2 1 0.000 -115.595786784 14.892952744 0.407402695 5.323804678 0.0000 0.02
3 2 0.000 -126.823748834 -11.227962049 0.115300517 1.591646800 0.0000 0.03
4 3 0.000 -150.870636785 -24.046887951 0.011394798 0.154813426 0.0000 0.02
5 4 0.000 -151.121829169 -0.251192384 0.004498398 0.037875784 0.0000 0.03
6 5 0.000 -150.900123989 0.221705180 0.008483436 0.119865266 0.0000 0.02
7 6 0.000 -151.582006133 -0.681882144 0.011892345 0.122063906 0.0000 0.02
8 7 0.000 -152.441656890 -0.859650757 0.007907887 0.062113717 0.0000 0.03
9 8 0.000 -152.729229838 -0.287572947 0.003318529 0.037884676 0.0000 0.02
10 2 0.000 -152.795374919 -0.066145081 0.005951772 0.054625652 0.0000 0.02
11 3 0.000 -152.839276725 -0.043901806 0.000860488 0.010210210 0.0000 0.03
12 4 0.000 -152.841131472 -0.001854746 0.000733951 0.007678730 0.0000 0.02
13 5 0.000 -152.841752921 -0.000621449 0.000348937 0.003519950 0.0000 0.02
14 6 0.000 -152.841816238 -0.000063316 0.000053288 0.000787592 0.0000 0.03
15 7 0.000 -152.841819180 -0.000002942 0.000021206 0.000157533 0.0000 0.02
16 8 0.000 -152.841819505 -0.000000325 0.000004796 0.000031694 0.0000 0.02
17 2 0.000 -152.841819522 -0.000000016 0.000000698 0.000005497 0.0000 0.03
18 3 0.000 -152.841819522 -0.000000000 0.000000236 0.000002276 0.0000 0.02
diis/vshift is closed at iter = 18
19 0 0.000 -152.8418195227 -0.000000000 0.000000078 0.000000848 0.0000 0.03
警告
这个算例分子输入坐标的单位是Bohr,必须使用关键词 unit=Bohr 指定坐标的长度单位为 Bohr 。
这个算例对应的高级输入为
$compass
geometry
C 0.1727682300 -0.0000045651 -0.8301598059
C -2.3763311896 0.0000001634 0.5600567139
H 0.0151760290 0.0000088544 -2.9110013387
H -2.0873396672 0.0000037621 2.5902220967
H -3.4601725077 -1.6628370597 0.0320271859
H -3.4601679801 1.6628382651 0.0320205364
O 2.2198078005 0.0000024315 0.2188182082
end geometry
unit # set unit of coordinates as Bohr
bohr
basis
6-31g
$end
$xuanyuan
$end
$scf
rhf
guess # ask for hcore guess
hcore
$end
备注
绝大部分情况下,Huckel和Hcore都不是最好的选择,因此除非万不得已,尽量不要使用Huckel和Hcore(尤其是后者)。
读入初始猜测轨道
BDF的SCF计算默认采用原子密度矩阵构建分子密度矩阵的方式产生初始猜测轨道。在实际计算中,用户可以读入已收敛的SCF分子轨道,做为当前SCF计算的初始猜测轨道。本算例中,我们先计算一个中性的 \(\ce{H2O}\) 分子,得到收敛轨道后,做为 \(\ce{H2O+}\) 离子的初始猜测轨道。
第一步,计算 \(\ce{H2O}\) 分子,准备输入文件,并命名为 h2o.inp 。内容如下:
#!bdf.sh
RKS/B3lyp/cc-pvdz
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
执行计算后,工作目录生成可读文件 h2o.scforb ,保存了SCF计算收敛的轨道.
第二步,利用 \(\ce{H2O}\) 分子的收敛轨道做为 \(\ce{H2O+}\) 离子计算的初始猜测,准备输入文件 h2o+.inp,内容如下:
#!bdf.sh
ROKS/B3lyp/cc-pvdz guess=readmo charge=1
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
%cp $BDF_WORKDIR/h2o.scforb $BDF_TMPDIR/${BDFTASK}.inporb
这里,使用了关键词 guess=readmo ,指定要读入初始猜测轨道。初始猜测轨道是用 % 引导的拷贝命令从
环境变量 BDF_WORKDIR 定义的文件夹中的h2o.scforb文件复制为 BDF_TMPDIR 中的 ${BDFTASK}.inporb 文件。
这里, BDF_WORKDIR 是执行计算任务的目录, BDF_TMPDIR 是BDF存储临时文件的目录。
与其它量子化学程序传递分子轨道
不同量子化学程序计算的分子轨道文件在原则上可以相互转化。BDF的 SCF 模块支持读入和存储 scforb 文件格式的分子轨道数据,可以通过 MOKIT(https://gitlab.com/jxzou/mokit)程序实现分子轨道文件转化,从而实现与其它量子化学程序之间传递分子轨道数据。
转化后的分子轨道文件能否正常使用,不仅依赖于原子顺序,坐标方位,以及点群对称性,还依赖于收缩函数的形式和排序,对于赝势基组还要看赝势数据是否一致。 如果有一处不一致,就会导致转化的分子轨道数据出现问题,无法达到加速收敛的目的。在基组方面,即便是同名的基组,由于原始数据的来源不同以及基组版本的差异, 计算的分子轨道数据也可能不一样,因此一定要仔细比较不同程序采用的基组是否完全一致。下面以H原子cc-pVTZ基组中的s收缩函数为例,列举了在比较基组时的几点注意事项。
****
H 1 2
S 5 3
3.387000E+01
5.095000E+00
1.159000E+00
3.258000E-01
1.027000E-01
6.068000E-03 0.000000E+00 0.000000E+00
4.530800E-02 0.000000E+00 0.000000E+00
2.028220E-01 0.000000E+00 0.000000E+00
0.0000000E+00 1.000000E+00 0.000000E+00
0.0000000E+00 0.000000E+00 1.000000E+00
P 2 2
(略)
注意
收缩函数的先后顺序在两个程序中是否一致? 如果把s函数的三列收缩因子互换,分子轨道因子的排序是不一样的。
每个收缩函数的收缩形式在两个程序中是否一致? 第一列收缩因子仅包含前三个s原函数,即(3s)/[1s],而在很多程序中是(4s)/[1s],那么对应的轨道因子就会有一些差别。
收缩因子相位在两个程序中是否一致? 这通常出现在非收缩函数的因子 1.0 中(见第二、三列),个别程序的内置基组可能会把收缩因子 1.0 写为 -1.0,导致轨道因子差个负号。
在使用赝势基组时,赝势的数据在两个程序中是否一致? 其中最典型的是 Def2系列基组的问题 。
为了保持基组的一致性,建议在 Compass 模块中用 ExpBas 输出基组,供其它量子化学程序使用。目前BDF支持输出 Molpro、Molcas、Gaussian、ORCA、CFour 五种基组格式。
除了以上因素之外,一些量子化学程序为了加速计算,会优先使用草稿文件夹下的临时数据文件,如果在此前的计算中恰好用了不一样的基组或者分子结构,会导致分子轨道文件非正常读取。 在BDF的计算中为了避免此类问题的发生,一般要在计算的开始把草稿文件夹清空,或者利用随机数生成新的草稿文件夹。
把小基组收敛轨道扩展为大基组初始猜测
初始猜测轨道可以由不同基组产生,同样可以加速计算收敛。这需要对初始猜测轨道文件进行扩展。 轨道扩展应该采用同组的基组,如cc-pVXZ系列、ANO-RCC系列等基组。 轨道扩展目前只支持高级输入模式。对于 \(\ce{CH3CHO}\) 分子,先用cc-pVDZ计算,然后将轨道扩展为cc-pVQZ基组计算的初始猜测轨道, 输入如下:
# First SCF calculation using small basis set cc-pvdz
$compass
geometry
C 0.1727682300 -0.0000045651 -0.8301598059
C -2.3763311896 0.0000001634 0.5600567139
H 0.0151760290 0.0000088544 -2.9110013387
H -2.0873396672 0.0000037621 2.5902220967
H -3.4601725077 -1.6628370597 0.0320271859
H -3.4601679801 1.6628382651 0.0320205364
O 2.2198078005 0.0000024315 0.2188182082
end geometry
basis
cc-pvdz
unit # set unit of coordinates as Bohr
Bohr
$end
$xuanyuan
$end
$scf
rhf
$end
#change chkfil name into chkfil1
%mv $BDF_WORKDIR/$BDFTASK.chkfil $BDF_WORKDIR/$BDFTASK.chkfil1
$compass
geometry
C 0.1727682300 -0.0000045651 -0.8301598059
C -2.3763311896 0.0000001634 0.5600567139
H 0.0151760290 0.0000088544 -2.9110013387
H -2.0873396672 0.0000037621 2.5902220967
H -3.4601725077 -1.6628370597 0.0320271859
H -3.4601679801 1.6628382651 0.0320205364
O 2.2198078005 0.0000024315 0.2188182082
end geometry
basis
cc-pvqz
unit
Bohr
$end
# change chkfil to chkfil1. notice, should use cp command since we will use
# "$BDFTASK.chkfil" in the next calculation
%cp $BDF_WORKDIR/$BDFTASK.chkfil $BDF_WORKDIR/$BDFTASK.chkfil2
# copy converged SCF orbital as input orbital of the module expandmo
%cp $BDF_WORKDIR/$BDFTASK.scforb $BDF_WORKDIR/$BDFTASK.inporb
# Expand orbital to large basis set. The output file is $BDFTASK.exporb
$expandmo
overlap
$end
$xuanyuan
$end
# use expanded orbital as initial guess orbital
%cp $BDF_WORKDIR/$BDFTASK.exporb $BDF_WORKDIR/$BDFTASK.scforb
$scf
RHF
guess
readmo
iprtmo
2
$end
上面的输入中,先使用 cc-pVDZ 基组执行第一个RHF计算,然后利用 expandmo 模块,将第一次 SCF 计算的收敛轨道扩展到 cc-pVQZ 基组,
最后利用 guess=readmo 做为SCF要读入的初始猜测轨道。
expandmo模块的输出为,
|******************************************************************************|
Start running module expandmo
Current time 2021-11-29 22:20:50
|******************************************************************************|
$expandmo
overlap
$end
/Users/bsuo/check/bdf/bdfpro/ch3cho_exporb.chkfil1
/Users/bsuo/check/bdf/bdfpro/ch3cho_exporb.chkfil2
/Users/bsuo/check/bdf/bdfpro/ch3cho_exporb.inporb
Expanding MO from small to large basis set or revise ...
1 Small basis sets
Number of basis functions (NBF): 62
Maxium NBF of shell : 6
Number of basis functions of small basis sets: 62
2 Large basis sets
Number of basis functions (NBF): 285
Maxium NBF of shell : 15
Overlap expanding : 1
Read guess orb
Read orbital title: TITLE - SCF Canonical Orbital
nsbas_small 62
nsbas_large 285
ipsmall 1
iplarge 1
Overlap of dual basis ...
Overlap of large basis ...
Write expanded MO to scratch file ...
|******************************************************************************|
Total cpu time: 0.42 S
Total system time: 0.02 S
Total wall time: 0.47 S
Current time 2021-11-29 22:20:51
End running module expandmo
|******************************************************************************|
可以看出,小基组有62个轨道,大基组有285个轨道,expandmo读入了SCF收敛的正则轨道,扩展到大基组并写入临时文件。
第二次SCF计算的输出为,
/Users/bsuo/check/bdf/bdfpro/ch3cho_exporb.scforb
Read guess orb: nden=1 nreps= 1 norb= 285 lenmo= 81225
Read orbital title: TITLE - orthognal Expand CMO
Orbitals initialization is completed.
........
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -152.952976892 122.547522034 0.002218985 0.246735859 0.0000 16.30
2 1 0.000 -152.983462881 -0.030485988 0.000367245 0.026196100 0.0000 16.83
3 2 0.000 -152.983976045 -0.000513164 0.000086429 0.006856831 0.0000 17.18
4 3 0.000 -152.984012062 -0.000036016 0.000016763 0.001472939 0.0000 17.02
5 4 0.000 -152.984019728 -0.000007666 0.000010400 0.001012788 0.0000 17.42
6 5 0.000 -152.984021773 -0.000002045 0.000003396 0.000328178 0.0000 17.28
7 6 0.000 -152.984022197 -0.000000423 0.000001082 0.000075914 0.0000 17.40
8 7 0.000 -152.984022242 -0.000000044 0.000000154 0.000008645 0.0000 17.28
9 8 0.000 -152.984022243 -0.000000001 0.000000066 0.000005087 0.0000 19.38
diis/vshift is closed at iter = 9
10 0 0.000 -152.984022243 -0.000000000 0.000000007 0.000000584 0.0000 18.95
Label CPU Time SYS Time Wall Time
SCF iteration time: 517.800 S 0.733 S 175.617 S
分子轨道最大占据数(mom)方法计算激发态
mom(maximum occupation method)是一种ΔSCF方法,可用于计算激发态。注意该方法的缩写为全小写字母,以和另一种ΔSCF方法——MOM(maximum overlap method)方法区分。
#----------------------------------------------------------------------
#
# mom method: J. Liu, Y. Zhang, and W. Liu, J. Chem. Theory Comput. 10, 2436 (2014).
#
# gs = -169.86584128
# ab = -169.62226127
# T = -169.62483480
# w(S)= 6.69eV
#----------------------------------------------------------------------
$COMPASS
Title
mom
Basis
6-311++GPP
Geometry
C 0.000000 0.418626 0.000000
H -0.460595 1.426053 0.000000
O 1.196516 0.242075 0.000000
N -0.936579 -0.568753 0.000000
H -0.634414 -1.530889 0.000000
H -1.921071 -0.362247 0.000000
End geometry
Check
$END
$XUANYUAN
$END
$SCF
UKS
DFT
B3LYP
alpha
10 2
beta
10 2
$END
%cp ${BDFTASK}.scforb $BDF_TMPDIR/${BDFTASK}.inporb
# delta scf with mom
$SCF
UKS
DFT
B3LYP
guess
readmo
alpha
10 2
beta
10 2
ifpair
hpalpha
1
10 0
11 0
iaufbau
2
$END
# pure delta scf for triplet
$SCF
UKS
DFT
B3LYP
alpha
11 2
beta
9 2
$END
这个算例执行了三次SCF计算,
第一次SCF,利用UKS方法计算甲酰胺分子的基态。输入利用alpha与beta两个关键词,分别指定了alpha和beta轨道的占据情况。甲酰胺分子基态是单重态S0,这里指定的alpha和beta占据情况相同。
10 2指定不可约表示A’与A”分别有10个和2个占据轨道。SCF模块将根据构造原理,按照轨道能量由低到高填充电子到轨道上。第二次SCF,利用UKS与mom方法计算甲酰胺分子的S1态。这里的关键点有:1 利用guess=readmo指定读入上一步UKS的收敛轨道;2 利用alpha、beta关键词设置了每个对称性轨道的占据数;3 设置了变量ifpair,需要和hpalpha,hpbeta联用,用于指定空穴-粒子(hole-particle - HP)轨道对的电子激发情况;4 设置了hpalpha变量,指定激发的HP轨道对。数字1表示激发一对HP轨道,下面的两行指定轨道激发情况,第一列表示在第一个不可约表示中把第10个alpha轨道的电子激发到第11个alpha轨道;第二列元素都为零,表示第二个不可约表示的轨道不做激发; 5 iaufbau变量设置为2,指定要进行mom计算。
第三次SCF,利用UKS方法计算甲酰胺分子的T1态。输入中,我们利用alpha和beta关键词指定轨道占据情况,其中alpha轨道的占据数为
11 2,表示对称性为A’和A”的alpha轨道上分别有11和2个电子占据, beta轨道的占据情况为9 2。 因为所要求解的态是给定的轨道占据数下能量最低的态,因此无需指定iaufbau。
这里,第一次SCF计算收敛结果为,
Superposition of atomic densities as initial guess.
skipaocheck T F
Solve HC=EC in pflmo space. F 12 75
Initial guess energy = -169.2529540680
[scf_cycle_init_ecdenpot]
Meomory for coulpotential 0.00 G
Start SCF iteration......
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -169.411739263 -0.158785195 0.005700928 0.163822560 0.0000 0.20
Turn on DFT calculation ...
2 1 0.000 -169.743175119 -0.331435856 0.008905349 0.340815886 0.0000 0.42
3 2 0.000 -169.232333660 0.510841459 0.006895796 0.296788710 0.0000 0.43
4 3 0.000 -169.863405142 -0.631071482 0.000364999 0.015732911 0.0000 0.43
5 4 0.000 -169.863345847 0.000059295 0.000209771 0.009205878 0.0000 0.42
6 5 0.000 -169.865811301 -0.002465454 0.000027325 0.000606909 0.0000 0.43
7 6 0.000 -169.865831953 -0.000020651 0.000008039 0.000357726 0.0000 0.43
8 7 0.000 -169.865833199 -0.000001246 0.000003927 0.000114311 0.0000 0.42
9 8 0.000 -169.865833401 -0.000000201 0.000000182 0.000004399 0.0000 0.43
diis/vshift is closed at iter = 9
10 0 0.000 -169.865833402 -0.000000000 0.000000139 0.000003885 0.0000 0.43
Label CPU Time SYS Time Wall Time
SCF iteration time: 8.650 S 0.700 S 4.050 S
Final DeltaE = -4.4343551053316332E-010
Final DeltaD = 1.3872600382452641E-007 5.0000000000000002E-005
Final scf result
E_tot = -169.86583340
E_ele = -241.07729109
E_nn = 71.21145769
E_1e = -371.80490197
E_ne = -541.14538673
E_kin = 169.34048477
E_ee = 148.48285541
E_xc = -17.75524454
Virial Theorem 2.003102
可以看出,第一次SCF计算使用了atom猜测,计算得到S0的能量为 -169.8658334023 a.u. 。第二次SCF计算读入了第一次SCF的收敛轨道, 并使用mom方法做SCF计算,输出文件先提示读入了分子轨道,并给出占据情况,
[Final occupation pattern: ]
Irreps: A' A''
detailed occupation for iden/irep: 1 1
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
detailed occupation for iden/irep: 1 2
1.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00
Alpha 10.00 2.00
这里, A' 不可约表示的第10个alpha轨道是占据轨道,第11个轨道是空轨道。第二次SCF计算读入了第一次SCF的收敛轨道,并使用mom方法做SCF计算,输入中要求将 A' 表示的第10个轨道的电子激发到第11个轨道上。输出文件先提示读入了分子轨道,并给出占据情况,
Read initial orbitals from user specified file.
/tmp/20117/mom_formamide.inporb
Read guess orb: nden=2 nreps= 2 norb= 87 lenmo= 4797
Read orbital title: TITLE - SCF Canonical Orbital
Initial occupation pattern: iden=1 irep= 1 norb(irep)= 66
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00
1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
Initial occupation pattern: iden=1 irep= 2 norb(irep)= 21
1.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00
Initial occupation pattern: iden=2 irep= 1 norb(irep)= 66
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
Initial occupation pattern: iden=2 irep= 2 norb(irep)= 21
1.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00
这里,iden=1为alpha轨道,irep=1指第一个不可约表示,总共有norb=66个轨道,其中,第10个轨道的占据数为0.00,第11个轨道占据数为1.00。经14次SCF迭代,收敛的S1态能量为 -169.6222628003 a.u.,如下所示:
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -169.505632070 125.031578610 0.020428031 1.463174456 0.0000 0.45
2 1 0.000 -169.034645773 0.470986296 0.036913522 1.562284831 0.0000 0.43
3 2 0.000 -165.750862892 3.283782881 0.032162782 1.516480990 0.0000 0.43
4 3 0.000 -169.560678610 -3.809815718 0.008588866 0.807859419 0.0000 0.43
5 4 0.000 -169.596211021 -0.035532411 0.003887621 0.367391029 0.0000 0.42
6 5 0.000 -169.620128518 -0.023917496 0.001826050 0.172456003 0.0000 0.43
7 6 0.000 -169.621976725 -0.001848206 0.000486763 0.044630527 0.0000 0.43
8 7 0.000 -169.622245116 -0.000268391 0.000113718 0.004980035 0.0000 0.43
9 8 0.000 -169.622261269 -0.000016153 0.000112261 0.009715905 0.0000 0.42
10 2 0.000 -169.622262553 -0.000001284 0.000043585 0.004092668 0.0000 0.42
11 3 0.000 -169.622262723 -0.000000169 0.000031601 0.002792075 0.0000 0.42
12 4 0.000 -169.622262790 -0.000000067 0.000010125 0.000848297 0.0000 0.43
13 5 0.000 -169.622262798 -0.000000007 0.000003300 0.000273339 0.0000 0.43
diis/vshift is closed at iter = 13
14 0 0.000 -169.622262800 -0.000000002 0.000001150 0.000079378 0.0000 0.42
Label CPU Time SYS Time Wall Time
SCF iteration time: 13.267 S 0.983 S 6.000 S
Final DeltaE = -1.8403909507469507E-009
Final DeltaD = 1.1501625138328933E-006 5.0000000000000002E-005
Final scf result
E_tot = -169.62226280
E_ele = -240.83372049
E_nn = 71.21145769
E_1e = -368.54021347
E_ne = -537.75897296
E_kin = 169.21875949
E_ee = 145.28871749
E_xc = -17.58222451
Virial Theorem 2.002385
[Final occupation pattern: ]
Irreps: A' A''
detailed occupation for iden/irep: 1 1
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00
1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00
SCF收敛后再一次打印轨道占据情况,可以看到 alpha 轨道中 A' 不可约表示的第10个轨道没有电子占据,第11个轨道有一个电子占据。
第三个SCF计算给出了 T1 态能量,为 -169.6248370697 a.u.,输出如下:
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -169.411739263 -0.158785195 0.083821477 9.141182225 0.0000 0.17
Turn on DFT calculation ...
2 1 0.000 -169.480549474 -0.068810211 0.066700318 6.978728919 0.0000 0.40
3 2 0.000 -169.277735673 0.202813801 0.014778190 0.648183923 0.0000 0.42
4 3 0.000 -169.613991196 -0.336255522 0.005923909 0.621843348 0.0000 0.42
5 4 0.000 -169.620096778 -0.006105582 0.001967168 0.164506160 0.0000 0.40
6 5 0.000 -169.623636999 -0.003540220 0.002722812 0.246425639 0.0000 0.42
7 6 0.000 -169.624704514 -0.001067515 0.001064536 0.098138798 0.0000 0.42
8 7 0.000 -169.624814882 -0.000110368 0.000525436 0.046392861 0.0000 0.42
9 8 0.000 -169.624834520 -0.000019637 0.000179234 0.012966641 0.0000 0.42
10 2 0.000 -169.624836694 -0.000002174 0.000063823 0.004902276 0.0000 0.42
11 3 0.000 -169.624836922 -0.000000227 0.000017831 0.001440089 0.0000 0.43
12 4 0.000 -169.624837025 -0.000000103 0.000034243 0.002618897 0.0000 0.42
13 5 0.000 -169.624837065 -0.000000039 0.000006158 0.000466001 0.0000 0.40
14 6 0.000 -169.624837068 -0.000000003 0.000003615 0.000354229 0.0000 0.42
diis/vshift is closed at iter = 14
15 0 0.000 -169.624837069 -0.000000001 0.000000966 0.000070404 0.0000 0.42
Label CPU Time SYS Time Wall Time
SCF iteration time: 13.150 S 0.950 S 5.967 S
Final DeltaE = -1.1375220765330596E-009
Final DeltaD = 9.6591808698539483E-007 5.0000000000000002E-005
Final scf result
E_tot = -169.62483707
E_ele = -240.83629476
E_nn = 71.21145769
E_1e = -368.57834907
E_ne = -537.80483706
E_kin = 169.22648799
E_ee = 145.32683246
E_xc = -17.58477815
Virial Theorem 2.002354
备注
对于某些体系的mom计算,BDF默认开启的SMH收敛算法可能反倒会阻碍收敛,此时可尝试在$scf块中加入NoSMH关键字,有一定概率会使得SCF收敛。如仍不奏效,可参照下节解决SCF不收敛问题的方法,来解决mom计算的收敛问题。
处理自洽场计算的不收敛问题
当SCF计算完成后,用户务必检查SCF是否收敛,只有在收敛的前提下才可以使用SCF计算的结果(能量,布居分析,轨道能等)以及进行后续的计算。注意SCF是否收敛不能仅从输出文件末尾有没有报错来判断,因为即便SCF不收敛,程序也不会立刻退出,而只是在SCF迭代的输出之后、SCF能量的输出之前,提示:
Warning !!! Total energy not converged!
而即便在这种情况下,程序仍然会在该信息之后打印能量、轨道信息、布居分析结果等,其中SCF能量后面会有 (NOT CONVERGED) 字样。虽然这些结果不能作为正式计算结果使用,但它们对于分析SCF不收敛的原因有一定帮助。
导致SCF不收敛的常见原因包括:
HOMO-LUMO能隙过小,导致前线轨道的占据情况反复变化。例如两个轨道 \(\psi_1\) 和 \(\psi_2\) ,在第N次SCF迭代时 \(\psi_1\) 为占据轨道, \(\psi_2\) 为空轨道,然而以这样的轨道占据情况为基础构建Fock矩阵并对角化后,得到的第N+1次SCF迭代的轨道,却是 \(\psi_1\) 的轨道能较 \(\psi_2\) 更高,因此电子从 \(\psi_1\) 轨道转移到 \(\psi_2\) 轨道。但这样一来,第N+1次SCF迭代的Fock矩阵相比第N次SCF迭代就会发生很大变化,导致在第N+2次SCF迭代时 \(\psi_1\) 的轨道能较 \(\psi_2\) 更低,于是轨道占据数又回到了第N次SCF迭代的情形,因而SCF迭代的轨道占据数总是在变化,始终不收敛。这种情况的典型表现为SCF能量交替在两个能量之间振荡(或在一定范围内无规律振荡),振荡幅度在 \(10^{-4} \sim 1\) Hartree左右,且SCF结束后打印的轨道占据数与预期不符。
HOMO-LUMO能隙较小,虽然各步迭代的轨道占据数没有变化,但轨道形状反复变化,导致SCF振荡不收敛。这种情况的典型表现与前一条类似,但振荡幅度一般稍小些,且SCF结束后打印的轨道占据数与预期定性相符。
数值积分格点过小或者双电子积分精度过低,导致SCF因数值误差而小幅度振荡不收敛。这种情况的典型表现为SCF能量以 \(10^{-4}\) Hartree以下的幅度无规律振荡,且SCF结束后打印的轨道占据数与预期定性相符。
基组接近线性相关,或因为格点太小导致基组在格点上的投影接近线性相关。这种情况的典型表现为SCF能量以1 Hartree以上的幅度变化(不一定是在振荡,也可能是单调或者基本单调的变化),SCF能量远低于预期值,且SCF结束后打印的轨道占据数完全不符合物理实际。当SCF能量较预期值低得非常多时,SCF能量甚至可能不显示为数字,而是显示为一串星号。
以下是各类SCF不收敛问题的常见解决方法(一定程度上也适用于BDF以外的软件):
增加能级移动vshift,适用于第1类和第2类情况,方法为在输入文件的$scf模块里加入:
vshift
0.2
如果仍然观察到明显的振荡,则逐渐增加vshift,直到收敛为止。vshift会倾向于让SCF的收敛变得单调,但是vshift设得太大会增加迭代收敛所用的次数,因此在增加vshift的时候可以适当增加maxiter。当vshift增加到1.0仍然无法收敛时,应该考虑其他方法。
增加密度矩阵阻尼damp,适用于第2类情况(对第1类情况也有一点效果),方法为在输入文件的$scf模块里加入:
damp
0.7
注意damp可以和vshift联用,两者的效果在一定程度上是相互促进的。如果阻尼设为0.7仍然观察到明显的振荡,则在保证阻尼小于1的情况下增大阻尼,例如接下来可以尝试0.9、0.95等。与vshift类似,damp也是倾向于改善SCF收敛的单调性,但damp太大会导致收敛变慢,因此可以增加maxiter。当damp增加到0.99仍然无法收敛时,应该考虑其他方法。
关闭DIIS,适用于第1类和第2类情况,且增加vshift和damp也无法收敛时。DIIS在大多数情况下是会加速SCF收敛的,但当HOMO-LUMO能隙特别小时有可能反倒会减慢甚至阻止收敛,后一种情况下可以在$scf模块里添加NoDIIS关键词关掉DIIS,增加maxiter,并视收敛情况设定vshift和damp。
关闭SMH,适用于第1类和第2类情况,且前3种方式都不奏效时,方法是在$scf模块里添加NoSMH关键词,增加maxiter,并视收敛情况设定vshift和damp。目前看来,起码对于基态计算而言,用SMH不收敛、不用SMH反倒能收敛的情形极其少,但是因为SMH是一种很新的SCF收敛方法,不排除极个别情况下SMH会对收敛有负面影响,因此关闭SMH可以作为一种备选方案。
改用FLMO或iOI方法,适用于第1类和第2类情况,分子较大(如大于50个原子),且怀疑SCF不收敛是因为原子初始猜测精度太低或者定性错误所导致时。方法请参见 FLMO及iOI方法相关章节 。
先计算一个类似的、较容易收敛的体系,再以该体系的波函数为初猜来收敛原体系,适用于第1类和第2类情况。比如一个中性的二重态过渡金属配合物的SCF计算不收敛,可以计算其闭壳层的一价阳离子,收敛后以一价阳离子的轨道作为初猜来进行中性分子的SCF计算(但注意因为BDF尚不支持读取RHF/RKS波函数作为UHF/UKS计算的初猜,因此此处闭壳层的一价阳离子应当用UHF/UKS计算)。极端情况下甚至可以先计算高价阳离子,然后添加少量(如2个)电子重新收敛SCF,再添加少量电子,如此直至得到原来的中性体系的波函数。另一种常用的手段为先在小基组下进行SCF计算,收敛后利用 expandmo模块 将小基组的SCF轨道投影到原基组上,再在原基组下进行SCF迭代直至收敛。
增大格点,适用于第3类情况,有时对第4类情况也有效。方法是用grid关键词,如:
grid
fine
注意:(1)对于meta-GGA泛函,默认的格点已经是fine了,因此此时应当将格点设为ultra fine;(2)增大格点会增加每一步SCF迭代的耗时;(3)增大格点会使得收敛的能量和其他没有改变grid的计算不可比,因此如果要将这个计算和以前做过的计算进行比较,或者将这个计算得到的能量/自由能与其他计算的结果作差等等,则必须把已经做过的所有相关计算用和本输入文件相同的格点重新计算,即便已经做过的那些计算不加大格点也能收敛,也需要这样做。加大格点后若结果没有任何改善,则应该尝试其他方法;如果结果有改善但还是不收敛,可以进一步尝试将fine改为ultra fine;如果仍然不能收敛,应当考虑下面的方法。
将双电子积分的阈值设严,适用于第3类情况,有时对第4类情况也有效。方法是在SCF模块里添加:
optscreen
1
该方法和增大格点一样,也会增大每一步SCF迭代的耗时,且也会导致计算结果和不加optscreen的计算结果不可比。该方法仅适用于不开启MPEC或MPEC+COSX的计算。
将判断基组线性相关性的阈值设松,适用于第4类情况。方法是在$scf模块里添加:
checklin
tollin
1.d-6
该方法会导致计算结果和不加这些关键词的计算结果不可比。tollin不建议设得比1.d-5更大,否则会引入较大误差,如果tollin设为1.d-5仍然出现第4类不收敛情况,则应考虑以上所述的增大格点、改变双电子积分阈值等方法。
注意在以上各方法中,如果某种方法虽不能使SCF收敛,但让SCF收敛情况较以前更好了,则尝试下一个方法时应当用
guess
readmo
读取上一种方法的最后一步SCF迭代的轨道作为初猜。但如果前一种方法反倒导致SCF收敛变差了,则尝试下一个方法时应当重新从原子猜测开始,或者挑选之前尝试过的其他方法的最后一步迭代的轨道作为初猜(当然这要求用户提前把每种SCF收敛方法得到的轨道都进行备份)。
自洽场计算的加速算法
BDF的一个重要特色是利用 MPEC+COSX 方法加速SCF、TDDFT的能量及梯度计算。设置MPEC+COSX计算,输入如下:
#! amylose2.sh
HF/cc-pvdz MPEC+COSX
Geometry
H -5.27726610038004 0.15767995434597 1.36892178079618
H -3.89542800401751 -2.74423996083456 -2.30130324998720
H -3.40930212959730 3.04543096108345 1.73325487719318
O -4.25161610042910 -0.18429704053319 1.49882079466485
H -4.12153806480025 0.39113300040060 -0.47267019103680
O -3.93883902709049 -2.16385597983528 -1.37984323910654
H -3.65755506365314 -2.55190701717719 0.56784675873394
H -2.66688104102718 -3.13999999152083 -0.32869523309397
O -3.68737510690803 2.57255697808269 0.79063986197194
H -2.16845111442446 1.40439897322928 1.59675986910159
H -0.80004208156425 3.67692503357694 -0.87083105709857
C -3.47036908085237 0.21757398797107 0.38361581865084
C -3.08081604941874 -2.23618399620817 -0.25179522317288
H -1.85215308213129 -1.05270701067006 0.92020982572454
C -2.73634509645279 1.50748698767418 0.67208385967460
O -0.95388209186676 2.93603601652216 -0.08659407523165
H -2.34176605974133 2.08883703173396 -1.35500112054343
C -2.46637306624908 -0.89337899823852 0.07760781649778
C -1.77582007601201 1.83730601785282 -0.45887211416401
O -1.70216504605578 -0.48600696920536 -1.07005315975028
H -0.26347504436884 0.90841605388912 -1.67304510231922
C -0.87599906000257 0.65569503172715 -0.80788211986139
H 1.05124197574425 -4.08129295376550 -0.80486617677089
H 1.91283792081157 2.93924205088598 -0.71300301703422
O 0.07007992244287 0.29718501862843 0.19143889205868
H 1.28488995808993 -0.48228594245462 -1.27588009910221
O 0.83243796215244 -3.05225096122844 -0.51820416035526
H 0.03099092283770 -2.15700599981123 1.08682384153403
H 0.99725792474852 -3.21082099855794 1.38542783977374
O 1.92550793896406 1.99389906198042 -1.25576903593383
H 2.32288890226196 1.52348902475463 0.72949896259198
H 5.42304993860699 1.71940008598879 -1.13583497057179
C 1.35508593454345 -0.11004196264200 -0.25348109013556
C 0.98581793175676 -2.43946398581436 0.75228585517262
H 1.91238990103301 -0.83125899736406 1.66788890655085
C 2.32240292575108 1.05122704465611 -0.25278704698785
O 4.65571492366175 1.63248206459704 -0.36643098789343
H 3.77658595927138 0.23304608296485 -1.60079803407907
C 1.86060292384221 -1.20698497780059 0.68314589788694
C 3.72997793572998 0.57134806164321 -0.56599702816882
O 3.14827793673614 -1.62888795836893 0.20457391544942
H 5.12279093584136 -0.96659193933436 0.00181296891020
C 4.14403492674986 -0.60389595307832 0.31494395641232
O 4.31314989648861 -0.29843197973243 1.69336596603165
H 3.37540288537848 0.07856300492440 2.10071295465512
End geometry
如果在高级输入模式下,只需在COMPASS模块输入中加入关键词 MPEC+COSX,如:
$compass
Geometry
H -5.27726610038004 0.15767995434597 1.36892178079618
H -3.89542800401751 -2.74423996083456 -2.30130324998720
H -3.40930212959730 3.04543096108345 1.73325487719318
O -4.25161610042910 -0.18429704053319 1.49882079466485
H -4.12153806480025 0.39113300040060 -0.47267019103680
O -3.93883902709049 -2.16385597983528 -1.37984323910654
H -3.65755506365314 -2.55190701717719 0.56784675873394
H -2.66688104102718 -3.13999999152083 -0.32869523309397
O -3.68737510690803 2.57255697808269 0.79063986197194
H -2.16845111442446 1.40439897322928 1.59675986910159
H -0.80004208156425 3.67692503357694 -0.87083105709857
C -3.47036908085237 0.21757398797107 0.38361581865084
C -3.08081604941874 -2.23618399620817 -0.25179522317288
H -1.85215308213129 -1.05270701067006 0.92020982572454
C -2.73634509645279 1.50748698767418 0.67208385967460
O -0.95388209186676 2.93603601652216 -0.08659407523165
H -2.34176605974133 2.08883703173396 -1.35500112054343
C -2.46637306624908 -0.89337899823852 0.07760781649778
C -1.77582007601201 1.83730601785282 -0.45887211416401
O -1.70216504605578 -0.48600696920536 -1.07005315975028
H -0.26347504436884 0.90841605388912 -1.67304510231922
C -0.87599906000257 0.65569503172715 -0.80788211986139
H 1.05124197574425 -4.08129295376550 -0.80486617677089
H 1.91283792081157 2.93924205088598 -0.71300301703422
O 0.07007992244287 0.29718501862843 0.19143889205868
H 1.28488995808993 -0.48228594245462 -1.27588009910221
O 0.83243796215244 -3.05225096122844 -0.51820416035526
H 0.03099092283770 -2.15700599981123 1.08682384153403
H 0.99725792474852 -3.21082099855794 1.38542783977374
O 1.92550793896406 1.99389906198042 -1.25576903593383
H 2.32288890226196 1.52348902475463 0.72949896259198
H 5.42304993860699 1.71940008598879 -1.13583497057179
C 1.35508593454345 -0.11004196264200 -0.25348109013556
C 0.98581793175676 -2.43946398581436 0.75228585517262
H 1.91238990103301 -0.83125899736406 1.66788890655085
C 2.32240292575108 1.05122704465611 -0.25278704698785
O 4.65571492366175 1.63248206459704 -0.36643098789343
H 3.77658595927138 0.23304608296485 -1.60079803407907
C 1.86060292384221 -1.20698497780059 0.68314589788694
C 3.72997793572998 0.57134806164321 -0.56599702816882
O 3.14827793673614 -1.62888795836893 0.20457391544942
H 5.12279093584136 -0.96659193933436 0.00181296891020
C 4.14403492674986 -0.60389595307832 0.31494395641232
O 4.31314989648861 -0.29843197973243 1.69336596603165
H 3.37540288537848 0.07856300492440 2.10071295465512
End geometry
Basis
cc-pvdz
MPEC+COSX # ask for the MPEC+COSX method
$end
在 SCF 模块会输出会有关 MPEC+COSX 是否都被设置为 True 的提示:
--- PRINT: Information about SCF Calculation ---
ICTRL_FRAGSCF= 0
IPRTMO= 1
MAXITER= 100
THRENE= 0.10E-07 THRDEN= 0.50E-05
DAMP= 0.00 VSHIFT= 0.00
IFDIIS= T
THRDIIS= 0.10E+01
MINDIIS= 2 MAXDIIS= 8
iCHECK= 0
iAUFBAU= 1
INIGUESS= 0
IfMPEC= T
IfCOSX= T
这里, IfMPEC= T , 且 IfCOSX= T 说明 MPEC+COSX 方法被用于计算。SCF迭代过程如下:
[scf_cycle_init_ecdenpot]
Meomory for coulpotential 0.02 G
Start SCF iteration......
Iter. idiis vshift SCF Energy DeltaE RMSDeltaD MaxDeltaD Damping Times(S)
1 0 0.000 -1299.6435521238 -23.7693069405 0.0062252375 0.2842668435 0.0000 2.69
2 1 0.000 -1290.1030630508 9.5404890730 0.0025508000 0.1065204344 0.0000 1.65
3 2 0.000 -1290.2258798561 -0.1228168053 0.0014087449 0.0742227520 0.0000 1.67
4 3 0.000 -1290.4879683983 -0.2620885422 0.0002338141 0.0153879051 0.0000 1.64
5 4 0.000 -1290.4955210658 -0.0075526675 0.0000713807 0.0049309441 0.0000 1.57
6 5 0.000 -1290.4966349620 -0.0011138962 0.0000156009 0.0010663736 0.0000 1.51
7 6 0.000 -1290.4966797420 -0.0000447800 0.0000043032 0.0002765334 0.0000 1.44
8 7 0.000 -1290.4966810419 -0.0000012999 0.0000014324 0.0000978302 0.0000 1.37
9 8 0.000 -1290.4966794202 0.0000016217 0.0000003030 0.0000173603 0.0000 1.40
10 2 0.000 -1290.4966902283 -0.0000108081 0.0000000659 0.0000034730 0.0000 1.11
diis/vshift is closed at iter = 10
11 0 0.000 -1290.5003691464 -0.0036789181 0.0000225953 0.0009032949 0.0000 5.85
Label CPU Time SYS Time Wall Time
SCF iteration time: 179.100 S 1.110 S 22.630 S
Final DeltaE = -3.678918126752251E-003
Final DeltaD = 2.259533940614071E-005 5.000000000000000E-005
Final scf result
E_tot = -1290.50036915
E_ele = -3626.68312754
E_nn = 2336.18275840
E_1e = -6428.96436179
E_ne = -7717.90756825
E_kin = 1288.94320647
E_ee = 2802.28123424
E_xc = 0.00000000
Virial Theorem 2.001208
在CPU为i9-9900K的台式机上,8个OpenMP线程并行计算耗时22秒。相同条件下SCF计算不用MPEC+COSX方法加速,计算耗时110秒, MPEC+COSX 大约加速了 5 倍。
大体系的iOI-SCF计算及FLMO方法
对于大体系(例如原子数大于300的体系),传统SCF计算方法常常不再适用,原因除了每步Fock矩阵构建时间变长以外,还包括以下因素:
Fock矩阵对角化时间占计算总时间的比例增加。当体系足够大时,每步Fock矩阵的构建时间与体系大小的平方成正比,但Fock矩阵对角化时间和体系大小的三次方成正比,因此对于特别大(如上千个原子)的体系,Fock矩阵对角化占总计算时间的比例将相当可观。
大体系的局部稳定波函数更多,导致大体系SCF计算收敛到用户期望的态的概率降低。换言之,SCF可能收敛到很多个不同的解,其中只有一个是用户想要的,因此增加了用户判断SCF解是否是自己期望的解,以及(如果收敛到非期望的解时)重新提交计算等时间开销。
大体系的SCF收敛比小体系更加困难,需要更多的迭代步数,甚至完全不能收敛。这除了是因为上述的局部稳定解变多以外,也有一部分原因是因为一般的基于原子密度的SCF初猜的质量随着体系增大而变差。
针对以上问题,一种解决方案是将体系分为若干片段(该过程称为分片;这些片段彼此之间可以重叠),对每个片段分别做SCF,再把所有片段的收敛的波函数汇总,作为总体系SCF计算的初猜。BDF的FLMO方法 (Fragment localized molecular orbital) 即属于一种基于分片的方法,其中每个片段的SCF收敛后,程序对每个片段的波函数进行局域化,再用所得的局域轨道产生总体系计算的初猜。相比不依赖局域轨道的分片方法,这样做会带来一些额外的好处:
SCF迭代可以在局域轨道基上进行,在局域轨道基下Fock矩阵无需进行全对角化,而只需进行块对角化,即转动轨道使得占据-空块为零即可,该步骤的计算量较全对角化小。
局域轨道基下的Fock矩阵的占据-空块非常稀疏,可以利用这种稀疏性进一步减小块对角化的计算量。
用户可以在进行全局SCF计算之前就指定某个局域轨道的占据数,从而选择性地得到该局域轨道占据或未占据的电子态,例如计算由一个Fe(II)和一个Fe(III)组成的金属团簇,可以通过指定Fe 3d轨道的占据数来控制哪个Fe收敛到二价组态,哪个Fe收敛到三价组态。在当前的BDF版本里实际还支持另外一种做法,即直接指定原子的形式氧化态和自旋态(见下)。出于便捷性考虑,一般建议用户直接通过原子的形式氧化态和自旋态来指定收敛到哪个电子态。
SCF计算直接得到收敛的局域轨道,而不是像一般的SCF计算那样只得到正则轨道。如果用户需要得到收敛的局域轨道来进行波函数分析等,那么FLMO方法相比传统的先得到正则轨道再进行局域化的做法而言,可以节省很多计算时间,也可以规避大体系局域化迭代次数多、容易不收敛的问题。
FLMO已被用于获得分子的定域化轨道、iOI-SCF、FLMO-MP2、O(1)-NMR等方法,还可以计算开壳层的单重态,用于研究单分子磁体等问题。
计算分片定域分子轨道FLMO(手动分片)
为了使用户对FLMO有个直观的了解,我们给出一个FLMO的计算示例。这里,我们要通过FLMO方法计算1,3,5,7-辛四烯 \(\ce{C8H10}\) 分子的定域化轨道。 我们先计算4个分子片,每个分子片是由中心原子、缓冲区原子(标记方式为在原子坐标后面加”B”,注意“B”和原子坐标之间必须有至少一个空格)和链接H原子(标记方式为在原子坐标后面加”L”,注意“L”和原子坐标之间必须有至少一个空格)组成。因分子结构较简单,这里的分子片是通过手动分片得到的,即每个分子片的中心原子为一个C=C双键及与其相连的所有氢原子,缓冲区原子为和该C=C双键直接相连的C=C双键及其所带的氢原子,也即分子片1和分子片4为1,3-丁二烯,分子片2和分子片3为1,3,5-己三烯。分子片SCF计算收敛后,通过Boys定域化方法得到分子片定域轨道。所有分子片计算完成后,再用四个分子片的定域轨道合成整体分子的pFLMO (primitive Fragment Localized Molecular Orbital)。利用pFLMO做初始猜测,计算整个 \(\ce{C8H10}\) 分子,并得到定域化的FLMO。输入示例如下:
###### Fragment 1
%echo "-------CHECKDATA: Calculate the 1st fragment -------------"
$COMPASS
Title
Fragment 1
Basis
6-31G
Geometry
c 0.5833330000 0.0 0.0000000000
c 1.9203330000 0.0 0.0000000000
h 0.0250410000 0.0 -0.9477920000
h 0.0250620000 0.0 0.9477570000
h 2.4703130000 0.0 -0.9525920000
c 2.6718330000 0.0 1.3016360000 B
c 4.0088330000 0.0 1.3016360000 B
h 4.7603330000 0.0 2.6032720000 L
h 2.1218540000 0.0 2.2542280000 B
h 4.5588130000 0.0 0.3490440000 B
End geometry
$END
$XUANYUAN
$END
$SCF
RHF
iprtmo
2
$END
$localmo
FLMO
$end
# copy pFLMO punch file
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_TMPDIR/fragment1
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_WORKDIR/fragment1
##### Fragment 2
%echo "-------CHECKDATA: Calculate the 2nd fragment -------------"
$COMPASS
Title
Fragment 2
Basis
6-31G
Geometry
c 0.5833330000 0.0 0.0000000000 B
c 1.9203330000 0.0 0.0000000000 B
h 0.0250410000 0.0 -0.9477920000 L
h 0.0250620000 0.0 0.9477570000 B
h 2.4703130000 0.0 -0.9525920000 B
c 2.6718330000 0.0 1.3016360000
c 4.0088330000 0.0 1.3016360000
h 2.1218540000 0.0 2.2542280000
h 4.5588130000 0.0 0.3490440000
c 4.7603330000 0.0 2.6032720000 B
c 6.0973330000 0.0 2.6032720000 B
h 4.2103540000 0.0 3.5558650000 B
h 6.6473130000 0.0 1.6506800000 B
h 6.8488330000 0.0 3.9049090000 L
End geometry
$END
$XUANYUAN
$END
$SCF
RHF
iprtmo
2
$END
$localmo
FLMO
$end
# copy pFLMO punch file
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_TMPDIR/fragment2
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_WORKDIR/fragment2
%ls -l $BDF_TMPDIR
%rm -rf $BDF_TMPDIR/$BDFTASK.*
# Fragment 3
%echo "-------CHECKDATA: Calculate the 3rd fragment -------------"
$COMPASS
Title
Fragment 3
Basis
6-31G
Geometry
c 2.6718330000 0.0 1.3016360000 B
c 4.0088330000 0.0 1.3016360000 B
h 1.9203330000 0.0 0.0000000000 L
h 2.1218540000 0.0 2.2542280000 B
h 4.5588130000 0.0 0.3490440000 B
c 4.7603330000 0.0 2.6032720000
c 6.0973330000 0.0 2.6032720000
h 4.2103540000 0.0 3.5558650000
h 6.6473130000 0.0 1.6506800000
c 6.8488330000 0.0 3.9049090000 B
c 8.1858330000 0.0 3.9049090000 B
h 6.2988540000 0.0 4.8575010000 B
h 8.7441260000 0.0 4.8527010000 L
h 8.7441050000 0.0 2.9571520000 B
End geometry
$END
$XUANYUAN
$END
$SCF
RHF
iprtmo
2
$END
# flmo_coef_gen=1, iprt=2, ipro=(6,7,8,9), icut=(3,13),
$localmo
FLMO
$end
# copy pFLMO punch file
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_TMPDIR/fragment3
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_WORKDIR/fragment3
%ls -l $BDF_TMPDIR
%rm -rf $BDF_TMPDIR/$BDFTASK.*
# Fragment 4
%echo "-------CHECKDATA: Calculate the 4th fragment -------------"
$COMPASS
Title
Fragment 4
Basis
6-31G
Geometry
h 4.0088330000 0.0 1.3016360000 L
c 4.7603330000 0.0 2.6032720000 B
c 6.0973330000 0.0 2.6032720000 B
h 4.2103540000 0.0 3.5558650000 B
h 6.6473130000 0.0 1.6506800000 B
c 6.8488330000 0.0 3.9049090000
c 8.1858330000 0.0 3.9049090000
h 6.2988540000 0.0 4.8575010000
h 8.7441260000 0.0 4.8527010000
h 8.7441050000 0.0 2.9571520000
End geometry
$END
$XUANYUAN
$END
$SCF
RHF
iprtmo
2
$END
# flmo_coef_gen=1, iprt=1, ipro=(6,7,8,9,10), icut=(1)
$localmo
FLMO
$end
# copy pFLMO punch file
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_TMPDIR/fragment4
%cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_WORKDIR/fragment4
%ls -l $BDF_TMPDIR
%rm -rf $BDF_TMPDIR/$BDFTASK.*
# Whole Molecule calculation
%echo "--------CHECKDATA: From fragment to molecular SCF calculation---------------"
$COMPASS
Title
Whole Molecule calculation
Basis
6-31G
Geometry
c 0.5833330000 0.0 0.0000000000
c 1.9203330000 0.0 0.0000000000
h 0.0250410000 0.0 -0.9477920000
h 0.0250620000 0.0 0.9477570000
h 2.4703130000 0.0 -0.9525920000
c 2.6718330000 0.0 1.3016360000
c 4.0088330000 0.0 1.3016360000
h 2.1218540000 0.0 2.2542280000
h 4.5588130000 0.0 0.3490440000
c 4.7603330000 0.0 2.6032720000
c 6.0973330000 0.0 2.6032720000
h 4.2103540000 0.0 3.5558650000
h 6.6473130000 0.0 1.6506800000
c 6.8488330000 0.0 3.9049090000
c 8.1858330000 0.0 3.9049090000
h 6.2988540000 0.0 4.8575010000
h 8.7441260000 0.0 4.8527010000
h 8.7441050000 0.0 2.9571520000
End geometry
Nfragment
4
Group
C(1)
$END
$XUANYUAN
$END
$SCF
RHF
FLMO
iprtmo
2
sylv
threshconv
1.d-8 1.d-6
$END
&DATABASE
fragment 1 9 # Fragment 1 with 9 atoms
1 2 3 4 5 6 7 8 9 # atom number in the whole molecule
fragment 2 12
1 2 4 5 6 7 8 9 10 11 12 13
fragment 3 12
6 7 8 9 10 11 12 13 14 15 16 18
fragment 4 9
10 11 12 13 14 15 16 17 18
&END
在输入中,我们给出了注释。每个分子片的计算由 compass、 xuanyuan 、 scf 及 localmo 四个模块构成。分别做预处理、积分计算、SCF计算和分子轨道定域化四个步骤,并通过在localmo模块后插入Shell命令
cp $BDF_WORKDIR/$BDFTASK.flmo $BDF_TMPDIR/fragment*
将存储定域轨道的文件 $BDFTASK.flmo 拷贝到 $BDF_TMPDIR 所在的目录备用。4个分子片段算完后是整体分子的计算,输入从
# Whole Molecule calculation
开始。在 compass 中,有关键词 Nfragment 4 ,提示要读入4个分子片,分子片信息在 &DATABASE 域中定义。
整体分子的SCF计算,首先会读入4个分子片的定域轨道,构建pFLMO,并给出轨道伸展系数 Mos (molecular orbital spread,某个定域轨道的Mos越大代表该定域轨道越离域,反之则代表该定域轨道越局域),如下:
Reading fragment information and mapping orbitals ...
Survived FLMO dims of frag( 11): 8 17 0 46 9
Survived FLMO dims of frag( 15): 8 16 0 66 12
Survived FLMO dims of frag( 15): 8 16 0 66 12
Survived FLMO dims of frag( 11): 8 17 0 46 9
Input Nr. of FLMOs (total, occ., soc., vir.) : 98 32 0 66
nmo != nbas
98 92
Local Occupied Orbitals Mos and Moc
Max_Mos: 1.89136758 Min_Mos: 0.31699600 Aver_Mos: 1.32004368
Local Virtual Orbitals Mos and Moc
Max_Mos: 2.46745638 Min_Mos: 1.46248295 Aver_Mos: 2.14404812
The prepared Nr. of pFLMOs (total, occ., vir.) : 98 32 0 66
Input Nr. of FLMOs (total, double-occ., single-occ, vir.) : 98 32 0 66
No. double-occ orbitals: 29
No. single-occ orbitals: 0
No. virtual orbitals: 63
iden= 1 29 63 32 66
Transfer dipole integral into Ao basis ...
Transfer quadrupole integral into Ao basis ...
Eliminate the occupied linear-dependent orbitals !
Max_Mos: 1.89136758 Min_Mos: 0.31699600 Aver_Mos: 1.32004368
3 linear dependent orbitals removed by preliminary scan
Initial MO/AO dimension are : 29 92
Finally 29 orbitals left. Number of cutted MO 0
Max_Mos: 1.89136758 Min_Mos: 0.31699600 Aver_Mos: 1.29690971
Perform Lowdin orthonormalization to occ pFLMOs
Project pFLMO occupied components out of virtual FLMOs
Max_Mos: 2.46467150 Min_Mos: 1.46222542 Aver_Mos: 2.14111949
3 linear dependent orbitals removed by preliminary scan
Initial NO, NV, AO dimension are : 29 63 92
Finally 92 orbitals left. Number of cutted MO 0
Max_Mos: 2.46467150 Min_Mos: 1.46222542 Aver_Mos: 2.15946681
Perform Lowdin orthonormalization to virtual pFLMOs 63
Local Occupied Orbitals Mos and Moc
Max_Mos: 1.88724854 Min_Mos: 0.31689707 Aver_Mos: 1.29604628
Local Virtual Orbitals Mos and Moc
Max_Mos: 2.53231018 Min_Mos: 1.46240853 Aver_Mos: 2.16493518
Prepare FLMO time : 0.03 S 0.02 S 0.05 S
Finish FLMO-SCF initial ...
可以看出,整体分子的pFLMO最大 Mos都小于2.6,不论占据或是虚轨道,pFLMO都是定域的。利用pFLMO做整体分子的初始猜测,进入SCF迭代,利用分块对角化方法保持对轨道的最小扰动,输出如下:
Check initial pFLMO orbital MOS
Local Occupied Orbitals Mos and Moc
Max_Mos: 1.88724854 Min_Mos: 0.31689707 Aver_Mos: 1.29604628
Local Virtual Orbitals Mos and Moc
Max_Mos: 2.53231018 Min_Mos: 1.46240853 Aver_Mos: 2.16493518
DNR !!
Final iter : 79 Norm of Febru 0.86590E-06
X --> U time: 0.000 0.000 0.000
block diag 0.017 0.000 0.017
block norm : 2.3273112079137773E-004
1 0 0.000 -308.562949067 397.366768902 0.002100841 0.027228292 0.0000 0.53
DNR !!
Final iter : 57 Norm of Febru 0.48415E-06
X --> U time: 0.000 0.000 0.017
block diag 0.000 0.000 0.017
block norm : 1.3067586006786384E-004
2 1 0.000 -308.571009930 -0.008060863 0.000263807 0.003230630 0.0000 0.52
DNR !!
Final iter : 43 Norm of Febru 0.64098E-06
X --> U time: 0.000 0.000 0.000
block diag 0.017 0.000 0.017
block norm : 3.6831175797520882E-005
SCF收敛后,系统会再一次打印分子轨道的Mos信息,
Print pFLMO occupation for checking ...
Occupied alpha obitals ...
Local Occupied Orbitals Mos and Moc
Max_Mos: 1.91280597 Min_Mos: 0.31692300 Aver_Mos: 1.30442588
Local Virtual Orbitals Mos and Moc
Max_Mos: 2.53288468 Min_Mos: 1.46274299 Aver_Mos: 2.16864691
Write FLMO coef into scratch file ... 214296
Reorder orbital via orbital energy ... 1 1
可以看出,最终FLMO的Mos与pFLMO相比变化不大,保持了很好的定域性。
以上的手动分片方法对于结构较复杂的分子来说比较繁琐,因为不仅需要手动给出每个分子片的定义,还需要在 &DATABASE 域中给出每个分子片和总体系的原子序号的对应关系。相比之下,更加方便的方法是使用以下的自动分片方法。
利用FLMO计算开壳层单重态(自动分片)
研究单分子磁体以及某些催化体系等,常遇到所谓反铁磁耦合的态,一般由两个自旋相反的电子以开壳层的形式占据在不同的原子中心(开壳层单重态),但也可能涉及多个单电子。BDF可以结合FLMO方法计算开壳层单重态。例如,下述算例采用FLMO方法计算一个含有Cu(II)和氮氧稳定自由基的体系的自旋破缺基态:
$autofrag
method
flmo
nprocs
2 # ask for 2 parallel processes to perform FLMO calculation
spinocc
# Set +1 spin population on atom 9 (O), set -1 spin population on atom 16 (Cu)
9 +1 16 -1
# Add no buffer atoms, except for those necessary for saturating dangling bonds.
# Minimizing the buffer radius helps keeping the spin centers localized in
# different fragments
radbuff
0
$end
$compass
Title
antiferromagnetically coupled nitroxide-Cu complex
Basis
LANL2DZ
Geometry
C -0.16158257 -0.34669203 1.16605797
C 0.02573099 -0.67120566 -1.13886544
H 0.90280854 -0.26733412 1.24138440
H -0.26508467 -1.69387001 -1.01851639
C -0.81912799 0.50687422 2.26635740
H -0.52831123 1.52953831 2.14600864
H -1.88351904 0.42751668 2.19103081
N -0.38402395 0.02569744 3.58546820
O 0.96884699 0.12656182 3.68120994
C -1.01167974 0.84046608 4.63575398
H -0.69497152 0.49022160 5.59592309
H -0.72086191 1.86312982 4.51540490
H -2.07607087 0.76110974 4.56042769
N -0.40937388 -0.19002965 -2.45797639
C -0.74875417 0.18529223 -3.48688305
Cu -1.32292113 0.82043400 -5.22772307
F -1.43762557 -0.29443417 -6.57175160
F -1.72615042 2.50823941 -5.45404079
H -0.45239892 -1.36935628 1.28640692
H 1.09012199 -0.59184704 -1.06353906
O -0.58484750 0.12139125 -0.11715881
End geometry
$end
$xuanyuan
$end
$scf
uks
dft
PBE0
spinmulti
1
D3
molden
$end
$localmo
FLMO
Pipek # Pipek-Mezey localization, recommended when pure sigma/pure pi LMOs are needed.
# Otherwise Boys is better
$end
FLMO计算目前不支持简洁输入。这个算例, autofrag 模块用于对分子自动分片,并产生FLMO计算的基本输入。BDF先根据 compass 模块中的分子结构与 autofrag 的参数定义信息产生分子片段,以及分子片段定域化轨道计算的输入文件。然后用分子片段的定域轨道组装整体分子的pFLMO (primitive Fragment Local Molecular Orbital) 作为全局SCF计算的初始猜测轨道,再通过全局SCF计算,在保持每一步迭代轨道都保持定域的前提下,得到整体分子的开壳层单重态。在计算中,为了输出简洁,分子片段计算输出保存为 ${BDFTASK}.framgmentN.out , N 为片段编号,标准输出只打印整体分子计算的输出。
输出会给出分子分片的信息,
----------- Buffered molecular fragments ----------
BMolefrag 1: [[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 19, 20, 21], [], [14], [14, 15], 0.0, 1.4700001016690913]
BMolefrag 2: [[14, 15, 16, 17, 18], [2, 4, 20], [21], [21], 0.0, 1.4700001016690913]
--------------------------------------------------------------------
Automatically assigned charges and spin multiplicities of fragments:
--------------------------------------------------------------------
Fragment Total No. of atoms Charge SpinMult SpinAlignment
1 17 0 2 Alpha
2 9 0 2 Beta
--------------------------------------------------------------------
Generate BDF input file ....
这里可以看出,我们产生了两个分子片段,指定了分子片 1 由17个原子组成,自旋多重度指认为2,分子片 2 由9个原子组成,自旋多重度也指认为2,但自旋方向和分子片 1 相反,也即beta电子比alpha电子多一个,而不是alpha电子比beta电子多一个。随后会分别计算2个分子片,提示信息如下(假设环境变量 OMP_NUM_THREADS 设为4):
Starting subsystem calculations ...
Number of parallel processes: 2
Number of OpenMP threads per process: 2
Please refer to test117.fragment*.out for detailed output
Total number of not yet converged subsystems: 2
List of not yet converged subsystems: [1, 2]
Finished calculating subsystem 2 ( 1 of 2)
Finished calculating subsystem 1 ( 2 of 2)
Starting global calculation ...
这要注意计算资源的设置。总的计算资源是进程数(Number of parallel processes)与每个进程的线程数(Number of OpenMP threads per process)的乘积,其中进程数是通过 autofrag 模块的 nprocs 关键词设定的,而总的计算资源是通过环境变量 OMP_NUM_THREADS 设定的,每个进程的线程数由程序自动通过总的计算资源除以进程数来得到。
整体分子的计算输出类似普通的SCF计算,但采用了分块对角化Fock矩阵的方法以保持轨道的定域性。
Check initial pFLMO orbital MOS
Openshell alpha :
Local Occupied Orbitals Mos and Moc
Max_Mos: 1.89684048 Min_Mos: 0.25791767 Aver_Mos: 1.15865182
Local Virtual Orbitals Mos and Moc
Max_Mos: 8.01038107 Min_Mos: 1.56092594 Aver_Mos: 3.04393282
Openshell beta :
Local Occupied Orbitals Mos and Moc
Max_Mos: 3.00463332 Min_Mos: 0.21757580 Aver_Mos: 1.24636228
Local Virtual Orbitals Mos and Moc
Max_Mos: 8.00411948 Min_Mos: 1.78248588 Aver_Mos: 3.04672070
...
1 0 0.000 -849.642342776 1158.171170064 0.046853948 4.840619682 0.5000 3.54
DNR !!
SDNR: warning: rotation angle too large, aborting
Final iter : 5 Norm of Febru 0.20133E+00
X --> U time: 0.000 0.000 0.000
block diag 0.000 0.000 0.000
block norm : 0.290774097871744
DNR !!
Final iter : 359 Norm of Febru 0.82790E-06
X --> U time: 0.000 0.000 0.000
block diag 0.020 0.000 0.010
block norm : 8.589840290871769E-003
迭代开始会给出轨道伸展 (Mos) 的信息, 数字越小,轨道定域性越好。SCF收敛后会再次打印 Mos 。 从布居分析的结果,
[Mulliken Population Analysis]
Atomic charges and Spin densities :
1C -0.2481 0.0010
2C -0.1514 0.0013
3H 0.2511 -0.0002
4H 0.2638 -0.0006
5C -0.3618 -0.0079
6H 0.2511 0.0240
7H 0.2436 -0.0013
8N 0.0128 0.3100
9O -0.2747 0.6562
10C -0.5938 -0.0092
11H 0.2696 0.0040
12H 0.2414 0.0242
13H 0.2302 -0.0016
14N 0.1529 -0.0202
15C -0.2730 0.0162
16Cu 0.8131 -0.5701
17F -0.5019 -0.2113
18F -0.4992 -0.2143
19H 0.2207 0.0008
20H 0.2666 -0.0000
21O -0.3128 -0.0008
Sum: -0.0000 0.0000
可看出,Cu原子的自旋密度为 -0.5701, 9O原子的自旋密度为 0.6562 ,其符号与预先指定的自旋相符,表明计算确实收敛到了所需要的开壳层单重态。注意此处自旋密度的绝对值小于1,说明Cu和9O上的自旋密度并不是严格定域在这两个原子上的,而是有一部分离域到了旁边的原子上。
在以上算例中, autofrag 模块输入的写法看似复杂,但是其中的 spinocc 和 radbuff 关键词对于FLMO方法而言不是必需的,也即以下写法的输入文件仍能成功运行,只不过不能确保Cu和O的自旋取向是用户指定的取向:
$autofrag
method
flmo
nprocs
2
$end
而 nprocs 表示对各个子体系的SCF计算进行并行化,以上述算例为例,即允许同时计算多个子体系,且任何时刻同时计算的子体系不超过2个。如果省略 nprocs 关键词,等价于将 nprocs 设为1,程序会依次计算所有子体系,每个子体系占用8个OpenMP线程,且每次待一个子体系计算结束后再计算下一个子体系。计算结果相比使用 nprocs 不会有任何区别,只是计算效率可能会有所降低。因此 nprocs 只影响FLMO计算的效率,而不影响其计算结果,也即以下写法同样可以成功运行,但计算时间可能比写 nprocs 略长:
$autofrag
method
flmo
$end
需要注意的是 nprocs 设置过大或过小,均可能导致计算时间增加。为讨论方便起见,假设在某较大分子的FLMO计算中,环境变量 OMP_NUM_THREADS 设定为8。则
nprocs
4
表示:
程序开始进行子体系计算时,会同时调用4个并发的BDF进程,每个进程计算一个子体系。如果子体系总数N小于4个,则只调用N个并发的BDF进程。
每个BDF进程使用2个OpenMP线程。当子体系总数小于4个时,有的子体系计算可能使用3个或4个OpenMP线程,但整个计算任务同时并发的OpenMP线程数始终不超过8个。
在计算刚开始时,整个计算恰好使用8个OpenMP线程,但随着计算接近结束,当只剩余不到4个子体系尚未计算完成时,整个计算所用的OpenMP线程数可能小于8个。
决定 nprocs 的最优值的因素主要有两个:
因OpenMP的并行效率一般低于100%,所以如果同时运行4个用时相同的任务,每个任务使用2个OpenMP线程,所用时间一般小于每个任务依次运行,且每个任务使用8个OpenMP线程所用的时间。
各个子体系的计算时间并不完全相同,甚至可能存在数倍的差别。仍以同时运行4个任务为例,如某些任务所用时间明显较其他任务长,则同时计算这4个子体系、每个子体系使用2个线程,可能反倒比依次计算、每个子体系使用8个线程更慢,因为当同时计算这4个子体系时,在计算后期一部分计算资源会闲置。这也就是所谓的负载均衡问题。
因此, nprocs 太小或太大,均有可能导致计算效率降低。一般 nprocs 设为子体系总数的1/5~1/3左右比较适宜,如在计算前对于系统产生的子体系数目没有一个适当的估计值,也可将 nprocs 简单地设为1、2等较小的正整数。例外情况是如果已知该计算的各个子体系计算量相仿的话, nprocs 可以设得大一些,例如在本小节开头的算例中,虽然只有两个子体系,但是其中较小的子体系含有过渡金属原子Cu,而较大的子体系是纯有机体系,因此两个子体系的计算时间相仿,可以同时计算。
iOI-SCF方法
iOI方法可以看作是FLMO方法的一种改进。在FLMO方法中,即便采用自动分片,用户仍然需要用 radcent 、 radbuff 等关键词指定分子片的大小,尽管这两个关键词都有默认值(分别是3.0和2.0),但无论是默认值还是用户指定的值,都不能保证对于当前体系是最优的。如果分子片太小,得到的定域轨道质量太差;如果分子片太大,又会导致计算量太大,以及定域化迭代不收敛。而iOI方法则是从比较小的分子片出发,不断增大、融合分子片,直至分子片刚好达到所需的大小为止,然后进行全局计算。其中每次增大、融合分子片称为一次宏迭代(Macro-iteration)。
示例如下:
$autofrag
method
ioi # To request a conventional FLMO calculation, change ioi to flmo
nprocs
2 # Use at most 2 parallel processes in calculating the subsystems
$end
$compass
Title
hydroxychloroquine (diprotonated)
Basis
6-31G(d)
Geometry # snapshot of GFN2-xTB molecular dynamics at 298 K
C -4.2028 -1.1506 2.9497
C -4.1974 -0.4473 4.1642
C -3.7828 0.9065 4.1812
C -3.4934 1.5454 2.9369
C -3.4838 0.8240 1.7363
C -3.7584 -0.5191 1.7505
H -4.6123 -0.8793 5.0715
C -3.3035 3.0061 2.9269
H -3.1684 1.2214 0.8030
H -3.7159 -1.1988 0.9297
C -3.1506 3.6292 4.2183
C -3.3495 2.9087 5.3473
H -2.8779 4.6687 4.2878
H -3.2554 3.3937 6.3124
N -3.5923 1.5989 5.4076
Cl -4.6402 -2.7763 3.0362
H -3.8651 1.0100 6.1859
N -3.3636 3.6632 1.7847
H -3.4286 2.9775 1.0366
C -3.5305 5.2960 -0.0482
H -2.4848 5.4392 -0.0261
H -3.5772 4.3876 -0.6303
C -4.1485 6.5393 -0.7839
H -3.8803 6.3760 -1.8559
H -5.2124 6.5750 -0.7031
C -3.4606 7.7754 -0.2653
H -2.3720 7.6699 -0.3034
H -3.7308 7.9469 0.7870
N -3.8415 8.9938 -1.0424
H -3.8246 8.8244 -2.0837
C -2.7415 9.9365 -0.7484
H -1.7736 9.4887 -0.8943
H -2.8723 10.2143 0.3196
C -2.7911 11.2324 -1.6563
H -1.7773 11.3908 -2.1393
H -3.5107 10.9108 -2.4646
H -3.0564 12.0823 -1.1142
C -5.1510 9.6033 -0.7836
H -5.5290 9.1358 0.1412
H -5.0054 10.6820 -0.6847
C -6.2224 9.3823 -1.8639
H -6.9636 10.1502 -1.7739
H -5.8611 9.4210 -2.8855
O -6.7773 8.0861 -1.6209
H -7.5145 7.9086 -2.2227
C -4.0308 4.9184 1.3736
H -3.7858 5.6522 2.1906
C -5.5414 4.6280 1.3533
H -5.8612 3.8081 0.7198
H -5.9086 4.3451 2.3469
H -6.1262 5.5024 1.0605
End geometry
MPEC+cosx # Accelerate the SCF iterations using MPEC+COSX. Not mandatory
$end
$xuanyuan
rs # the range separation parameter omega (or mu) of wB97X
0.3
$end
$scf
rks
dft
wB97X
iprt # Increase print level for more verbose output. Not mandatory
2
charge
2
$end
$localmo
FLMO
$end
注意在iOI计算中, nprocs 关键词的含义和FLMO计算相同,也需要根据分子的大小来选择合适的值,且 nprocs 的不同取值仍然只是影响计算速度而不影响计算结果。和FLMO计算的区别在于,iOI计算涉及多步宏迭代(见下),每步宏迭代的子体系数目是逐步减小的,因此 nprocs 的最优取值应当保守一些,例如取为第0步宏迭代子体系数目的1/10~1/5。
程序一开始将该分子分为5个分子片:
----------- Buffered molecular fragments ----------
BMolefrag 1: [[4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 18, 19], [1, 16, 2, 3, 7, 15, 17, 46, 47, 48, 49, 50, 51], [20], [20, 21, 22, 23], 2.0, 2.193]
BMolefrag 2: [[20, 21, 22, 23, 24, 25, 26, 27, 28, 46, 47, 48, 49, 50, 51], [18, 19, 29, 30], [8, 31, 38], [8, 4, 11, 31, 32, 33, 34, 38, 39, 40, 41], 2.0, 2.037]
BMolefrag 3: [[2, 3, 7, 15, 17], [1, 16, 4, 8, 5, 6, 9, 10, 11, 12, 13, 14], [18], [18, 19, 46], 2.0, 3.5]
BMolefrag 4: [[29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45], [23, 24, 25, 26, 27, 28, 20, 21, 22], [46], [46, 18, 47, 48], 2.0, 3.386]
BMolefrag 5: [[1, 16], [2, 3, 7, 5, 6, 9, 10, 4, 8], [15, 11, 18], [15, 12, 17, 11, 13, 18, 19, 46], 2.0, 2.12]
--------------------------------------------------------------------
Automatically assigned charges and spin multiplicities of fragments:
--------------------------------------------------------------------
Fragment Total No. of atoms Charge SpinMult SpinAlignment
1 26 1 1 N.A.
2 22 1 1 N.A.
3 18 1 1 N.A.
4 27 1 1 N.A.
5 14 1 1 N.A.
--------------------------------------------------------------------
这里SpinAlignment显示为N.A.,是因为所有分子片都是闭壳层的,因此不存在自旋取向的问题。
之后开始进行子体系计算,
Starting subsystem calculations ...
Number of parallel processes: 2
Number of OpenMP threads per process: 2
Please refer to test106.fragment*.out for detailed output
Macro-iter 0:
Total number of not yet converged subsystems: 5
List of not yet converged subsystems: [4, 1, 2, 3, 5]
Finished calculating subsystem 4 ( 1 of 5)
Finished calculating subsystem 2 ( 2 of 5)
Finished calculating subsystem 1 ( 3 of 5)
Finished calculating subsystem 5 ( 4 of 5)
Finished calculating subsystem 3 ( 5 of 5)
Maximum population of LMO tail: 110.00000
======================================
Elapsed time of post-processing: 0.10 s
Total elapsed time of this iteration: 34.28 s
此后程序将这5个分子片进行两两融合,并扩大缓冲区,得到3个较大的子体系。这3个较大的子体系的定义在 ${BDFTASK}.ioienlarge.out 里给出:
Finding the optimum iOI merge plan...
Initial guess merge plan...
Iter 0 Number of permutations done: 1
New center fragments (in terms of old center fragments):
Fragment 1: 5 3
NBas: 164 184
Fragment 2: 2 4
NBas: 164 174
Fragment 3: 1
NBas: 236
Center fragment construction done, total elapsed time 0.01 s
Subsystem construction done, total elapsed time 0.01 s
也即新的子体系1是由旧的子体系5、3融合(并扩大缓冲区)得到的,新的子体系2是由旧的子体系2、4融合(并扩大缓冲区)得到的,而新的子体系3则直接由旧的子体系1扩大缓冲区而得到。然后以原来5个较小子体系的收敛的定域轨道作为初猜,进行这些较大子体系的SCF计算:
Macro-iter 1:
Total number of not yet converged subsystems: 3
List of not yet converged subsystems: [2, 3, 1]
Finished calculating subsystem 3 ( 1 of 3)
Finished calculating subsystem 1 ( 2 of 3)
Finished calculating subsystem 2 ( 3 of 3)
Fragment 1 has converged
Fragment 2 has converged
Fragment 3 has converged
Maximum population of LMO tail: 0.04804
======================================
*** iOI macro-iteration converged! ***
Elapsed time of post-processing: 0.04 s
Total elapsed time of this iteration: 33.71 s
此时程序自动判断这些子体系的大小已经足以将体系的LMO收敛到所需精度,因而iOI宏迭代收敛,进行iOI全局计算。iOI全局计算的输出与FLMO全局计算类似,但为了进一步加快Fock矩阵的块对角化,在iOI全局计算里,某些已经收敛的LMO会被冻结,从而降低需要块对角化的Fock矩阵的维度,但也引入了少许误差(一般在 \(10^{-6} \sim 10^{-5}\) Hartree数量级)。以最后一步SCF迭代为例:
DNR !!
47 of 90 occupied and 201 of 292 virtual orbitals frozen
SDNR. Preparation: 0.01 0.00 0.00
norm and abs(maximum value) of Febru 0.35816E-03 0.11420E-03 gap = 1.14531
Survived/total Fia = 472 3913
norm and abs(maximum value) of Febru 0.36495E-03 0.11420E-03 gap = 1.14531
Survived/total Fia = 443 3913
norm and abs(maximum value) of Febru 0.16908E-03 0.92361E-04 gap = 1.14531
Survived/total Fia = 615 3913
norm and abs(maximum value) of Febru 0.11957E-03 0.21708E-04 gap = 1.14531
Survived/total Fia = 824 3913
norm and abs(maximum value) of Febru 0.68940E-04 0.15155E-04 gap = 1.14531
Survived/total Fia = 965 3913
norm and abs(maximum value) of Febru 0.56539E-04 0.15506E-04 gap = 1.14531
Survived/total Fia = 737 3913
norm and abs(maximum value) of Febru 0.30450E-04 0.62094E-05 gap = 1.14531
Survived/total Fia = 1050 3913
norm and abs(maximum value) of Febru 0.36500E-04 0.82498E-05 gap = 1.14531
Survived/total Fia = 499 3913
norm and abs(maximum value) of Febru 0.14018E-04 0.38171E-05 gap = 1.14531
Survived/total Fia = 1324 3913
norm and abs(maximum value) of Febru 0.43467E-04 0.15621E-04 gap = 1.14531
Survived/total Fia = 303 3913
norm and abs(maximum value) of Febru 0.12151E-04 0.26221E-05 gap = 1.14531
Survived/total Fia = 837 3913
norm and abs(maximum value) of Febru 0.15880E-04 0.82575E-05 gap = 1.14531
Survived/total Fia = 185 3913
norm and abs(maximum value) of Febru 0.52265E-05 0.71076E-06 gap = 1.14531
Survived/total Fia = 1407 3913
norm and abs(maximum value) of Febru 0.31827E-04 0.12985E-04 gap = 1.14531
Survived/total Fia = 253 3913
norm and abs(maximum value) of Febru 0.77674E-05 0.24860E-05 gap = 1.14531
Survived/total Fia = 650 3913
norm and abs(maximum value) of Febru 0.56782E-05 0.38053E-05 gap = 1.14531
Survived/total Fia = 264 3913
SDNR. Iter: 0.01 0.00 0.00
Final iter : 16 Norm of Febru 0.25948E-05
X --> U time: 0.000 0.000 0.000
SDNR. XcontrU: 0.00 0.00 0.00
block diag 0.020 0.000 0.000
block norm : 2.321380955939448E-004
Predicted total energy change: -0.0000000659
9 0 0.000 -1401.6261867529 -0.0011407955 0.0000016329 0.0000904023 0.0000 16.97
即冻结了47个占据轨道和201个虚轨道。
iOI全局计算SCF收敛后,可以仿照一般SCF计算的输出文件读取能量、布居分析等信息,此处不再赘述。
含时密度泛函理论
BDF支持多种激发态计算方法,其中以基于Kohn-Sham参考态的线性响应含时密度泛函 (TDDFT)方法,以及TDDFT方法的Tamm-Dancoff近似(TDA)为主。与其他量化软件相比,BDF的TDDFT模块独具特色,主要体现在:
支持各种自旋翻转(spin-flip)方法;
支持自旋匹配TDDFT方法X-TDDFT,可以有效解决参考态为开壳层时激发态存在自旋污染的问题,适用于自由基、过渡金属等体系的激发态计算;
支持芯激发态(core excited state)相关的计算,如计算X射线吸收谱(XAS)。一般的TDDFT算法为了计算一个激发态,常需同时把比该激发态激发能更低的所有态均计算出来,而芯激发态的能量通常很高,这样计算效率太低。BDF所用的iVI方法则可在不计算更低的激发态的情况下,直接计算某个较高的能量区间内的所有激发态,从而节省计算资源;
支持一阶非绝热耦合矩阵元(first-order non-adiabatic coupling matrix element, fo-NACME,或简称NACME)的计算,尤其是激发态和激发态之间的NACME。NACME主要用于研究非辐射跃迁过程,如结合MOMAP软件用费米黄金规则计算内转换速率常数(见 示例 ),或用非绝热动力学研究内转换、光化学反应的过程等等。很多量子化学程序支持基态和激发态之间的NACME,但支持激发态和激发态之间的NACME的程序较少,因此对于激发态到激发态的内转换以及多态光化学反应等过程,BDF相比现有大部分量子化学程序有独特的优势。
除TDDFT之外,BDF还支持利用 mom方法 在SCF水平下计算激发态。
危险
所有 SCAN 家族的泛函(如SCAN0,r2SCAN)都存在“三重态不稳定”问题 [66] , 不要用于TDDFT自旋翻转计算(例如对闭壳层体系计算三重激发态)。这种情况推荐用TDA。
闭壳层体系计算:R-TDDFT
R-TDDFT用于计算闭壳层体系。如果基态计算从RHF出发,TDDFT模块执行的是TDHF计算。 利用TDDFT计算 \(\ce{H2O}\) 分子激发能,简洁输入如下:
#!bdf.sh
TDDFT/B3lyp/cc-pvdz iroot=1
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
这里,关键词 TDDFT/B3lyp/cc-pvdz 指定执行TDDFT计算,所用泛函为 B3lyp ,基组为 cc-pVDZ 。
与之对应的高级输入为:
$compass
Geometry
O
H 1 1.0
H 1 1.0 2 109.
End geometry
Basis
cc-pvdz
$end
$xuanyuan
$end
$scf
RKS # Restricted Kohn-sham
DFT # DFT exchange-correlation functional B3lyp
b3lyp
$end
# input for tddft
$tddft
iroot # For each irrep, calculate 1 root.
1 #on default, 10 roots are calculated for each irreps if advanced input used
$end
完成计算将顺序调用 COMPASS , XUANYUAN , SCF 及 TDDFT 四个模块。其中 SCF 模块执行RKS计算。 基于RKS的计算结果,进行后续的 TDDFT 计算。
注意因为水分子属于 \(\rm C_{2v}\) 点群,共有4个不可约表示,而不同不可约表示的激发态是分别求解的,因此视用户需求而定,有以下若干种指定激发态数目的方法,例如:
(1)每个不可约表示均计算1个激发态:
$TDDFT
iroot
1
$END
此时每个不可约表示计算得到的激发态大概率是该不可约表示下能量最低的激发态,但是这一点无法保证,也就是说有较小的概率会收敛到第二激发态甚至更高的某个激发态。如果要提高得到最低激发态的概率,可以写
$TDDFT
iroot
2
$END
此时每个不可约表示计算2个激发态,且每个不可约表示下计算得到的第一个激发态是该不可约表示下能量最低的激发态的概率较iroot=1时更高。此外,此时每个不可约表示下计算得到的第二个激发态大概率是该不可约表示下能量第二低的激发态,但满足这一点的概率较“计算得到的第一个激发态是该不可约表示下能量最低的激发态”的概率更低。如果进一步增加iroot,则计算得到的第一个激发态是能量最低的激发态的概率很快趋近于100%,但永远无法严格达到100%。
出于类似的原因,不仅当计算1个激发态时常常需要将iroot设为大于1,当计算N(N>1)个激发态时,若想相对可靠地确保这N个激发态是能量最低的N个激发态,也需要将iroot设为大于N。一般而言,当分子满足下述条件之一时,应当将iroot设得较大,例如比所需的激发态数目大至少3个:(1)分子具有近似的点群对称性;(2)分子虽然具有精确的点群对称性,但是受程序限制或者应用户需要,计算在更低的点群下进行,例如在开壳层TDDFT(见下文)计算中,因开壳层TDDFT代码不支持非阿贝尔点群,而改为在最大的阿贝尔子群下进行计算。当分子不属于上述情况之一时,iroot只需比所需的激发态数目略大即可,例如大1~2个。
(2)只计算一个B1激发态和一个B2激发态,不计算其他不可约表示下的激发态:
#! tdtest.sh
TDDFT/B3lyp/3-21G nroot=0,0,1,1
Geometry
...
End geometry
或者
$TDDFT
nroot
0 0 1 1 # 也可输入为 0,0,1,1
$END
其中nroot关键词表明用户分别对每个不可约表示指定激发态的数目。因程序内部将 \(\rm C_{2v}\) 点群的不可约表示以A1、A2、B1、B2的顺序排列(见点群相关章节关于各个不可约表示的排序的介绍),因此以上输入表明只计算B1、B2各一个激发态。类似iroot的情形,如需要相对可靠地确保计算得到的是相应不可约表示下能量最低的态,则应当将nroot设得比所需值略大。
(3)计算最低的4个激发态,而不限定这些激发态的不可约表示
#! tdtest.sh
TDDFT/B3lyp/3-21G iroot=-4
Geometry
...
End geometry
或者
$TDDFT
iroot
-4
$END
此时程序通过初始猜测的激发能来判断各个不可约表示应当求解多少个激发态,但因为初始猜测的激发能排列顺序可能和完全收敛的激发能有一定差异,程序不能严格保证求得的4个激发态一定是能量最低的4个激发态。如用户要求严格保证得到的4个激发态为最低的4个激发态,用户应当令程序计算多于4个激发态,如8个激发态,然后取能量最低的4个。
Kohn-Sham计算的输出前面已经介绍过,这里我们只关注 TDDFT 计算的结果。程序输出会先给出TDDFT计算的设置信息,方便用户检查是否计算的设置,如下:
--------------------------------------------------
--- PRINT: Information about TDDFT calculation ---
--------------------------------------------------
ERI Maxblk= 8M
[print level]
iprt= 0
[method]
R-TD-DFT
isf= 0
SC Excitations
RPA: (A-B)(A+B)Z=w2*Z
[special choice for method]
ialda= 0
[active space]
Full active space
[algorithm]
Target Excited State in each rep / Diag method :
1 A1 1 1
2 A2 1 1
3 B1 1 1
4 B2 1 1
[dvdson_parameters]
iupdate = 3
Nfac = 50
Nmaxcycle= 50
nblock = 50
crit_e = 0.10E-06
crit_vec = 0.10E-04
crit_demo= 0.10E-07
crit_indp= 0.10E-09
guess = 20
dump = 0
[output eigenvector control]
cthrd= 0.100
-------------------------------------------------
--- END : Information about TDDFT calculation ---
-------------------------------------------------
这里,
R-TD-DFT表示正在进行的是基于限制性基态波函数计算的TDDFT;isf= 0表示计算不翻转自旋;ialda= 0表示使用Full non-collinear Kernel,这是非自旋翻转TDDFT的默认Kernel。
下面的输出给出了每个不可约表示计算的根的数目。
Target Excited State in each rep / Diag method :
1 A1 1 1
2 A2 1 1
3 B1 1 1
4 B2 1 1
TDDFT模块还会打印占据轨道,虚轨道等TDDFT计算的活性轨道信息
Print [Active] Orbital List
---[Alpha set]---
idx irep (rep,ibas,type) F_av(eV) iact
---------------------------------------------------
1 1 A1 1 2 -520.34813 0.05
2 1 A1 2 2 -26.42196 1.84
3 3 B1 1 2 -13.66589 2.96
4 1 A1 3 2 -9.50404 2.49
5 4 B2 1 2 -7.62124 2.12
6 1 A1 4 0 1.23186 9.86
7 3 B1 2 0 3.27539 11.48
8 3 B1 3 0 15.02893 7.40
9 1 A1 5 0 15.44682 6.60
10 1 A1 6 0 24.53525 4.35
11 4 B2 2 0 25.07569 3.88
12 3 B1 4 0 27.07545 6.17
13 2 A2 1 0 33.09515 3.99
14 1 A1 7 0 34.03695 5.08
15 4 B2 3 0 39.36812 4.67
16 3 B1 5 0 43.83066 4.86
17 1 A1 8 0 43.91179 4.34
18 3 B1 6 0 55.56126 4.35
19 1 A1 9 0 56.13188 4.04
20 4 B2 4 0 78.06511 2.06
21 2 A2 2 0 80.16952 2.10
22 1 A1 10 0 83.17934 2.38
23 1 A1 11 0 94.37171 2.81
24 3 B1 7 0 99.90789 2.86
这里,轨道1-5是占据轨道,6-24是虚轨道,其中,第5个和第6个轨道分别是HOMO和LUMO轨道, 分别属于不可约表示B2和不可约表示A1, 轨道能分别是-7.62124 eV和1.23186 eV。由于 \(\ce{H2O}\) 分子有4个不可约表示,TDDFT会对每个不可约表示逐一求解。 在进入Davidson迭代求解Casida方程之前,系统会估计内存使用情况,
==============================================
Jrep: 1 ExctSym: A1 (convert to td-psym)
Irep: 1 PairSym: A1 GsSym: A1
Nexit: 1 Nsos: 33
==============================================
Estimated memory for JK operator: 0.053 M
Maxium memory to calculate JK operator: 512.000 M
Allow to calculate 1 roots at one pass for RPA ...
Allow to calculate 2 roots at one pass for TDA ...
Nlarge= 33 Nlimdim= 33 Nfac= 50
Estimated mem for dvdson storage (RPA) = 0.042 M 0.000 G
Estimated mem for dvdson storage (TDA) = 0.017 M 0.000 G
这里,系统统计存储JK算符需要的内存约 0.053MB, 输入设置的内存是512MB (见 memjkop 关键词 )。
系统提示RPA计算,即完全的TDDFT计算每次(one pass)可以算1个根,TDA计算每次可以算2个根。由于分子体系小,内存足够。
分子体系较大时,如果这里输出的允许的每次可算根的数目小于系统设置数目,TDDFT模块将根据最大允许可算根的数目,通过
多次积分计算构造JK算符,导致计算效率降低,用户需要用 memjkop 关键词增加内存。
Davidson迭代开始计算输出信息如下,
Iteration started !
Niter= 1 Nlarge = 33 Nmv = 2
Ndim = 2 Nlimdim= 33 Nres= 31
Approximated Eigenvalue (i,w,diff/eV,diff/a.u.):
1 9.5246226546 9.5246226546 0.350E+00
No. of converged eigval: 0
Norm of Residuals:
1 0.0120867135 0.0549049429 0.121E-01 0.549E-01
No. of converged eigvec: 0
Max norm of residues : 0.549E-01
*** New Directions : sTDDFT-Davidson step ***
Left Nindp= 1
Right Nindp= 1
Total Nindp= 2
[tddft_dvdson_ZYNI]
Timing For TDDFT_AVmat, Total: 0.08s 0.02s 0.02s
MTrans1: 0.00s 0.02s 0.00s
COULPOT: 0.00s 0.00s 0.00s
AVint : 0.08s 0.00s 0.02s
MTrans2: 0.00s 0.00s 0.00s
TDDFT ZYNI-AV time-TOTAL 0.08 S 0.02 S 0.02 S
TDDFT ZYNI-AV time-Coulp 0.08 S 0.02 S 0.02 S
TDDFT ZYNI-AV time-JKcon 0.00 S 0.00 S 0.00 S
tddft JK operator time: 0.00 S 0.00 S 0.00 S
Niter= 2 Nlarge = 33 Nmv = 4
Ndim = 4 Nlimdim= 33 Nres= 29
Approximated Eigenvalue (i,w,diff/eV,diff/a.u.):
1 9.3817966321 0.1428260225 0.525E-02
No. of converged eigval: 0
Norm of Residuals:
1 0.0029082582 0.0074085379 0.291E-02 0.741E-02
No. of converged eigvec: 0
收敛信息如下:
Niter= 5 Nlarge = 33 Nmv = 10
Ndim = 10 Nlimdim= 33 Nres= 23
Approximated Eigenvalue (i,w,diff/eV,diff/a.u.):
1 9.3784431931 0.0000001957 0.719E-08
No. of converged eigval: 1
### Cong: Eigenvalues have Converged ! ###
Norm of Residuals:
1 0.0000009432 0.0000023006 0.943E-06 0.230E-05
No. of converged eigvec: 1
Max norm of residues : 0.230E-05
### Cong. Residuals Converged ! ###
------------------------------------------------------------------
Orthogonality check2 for iblock/dim = 0 1
Averaged nHxProd = 10.000
Ndim = 1 Maximum nonzero deviation from Iden = 0.333E-15
------------------------------------------------------------------
------------------------------------------------------------------
Statistics for [dvdson_rpa_block]:
No. of blocks = 1
Size of blocks = 50
No. of eigens = 1
No. of HxProd = 10 Averaged = 10.000
Eigenvalues (a.u.) =
0.3446513056
------------------------------------------------------------------
从上面输出的第一行可以看出,5次迭代计算收敛。系统随后打印收敛后电子态的信息,
No. 1 w=9.3784 eV -76.0358398606 a.u. f= 0.0767 D<Pab>= 0.0000 Ova= 0.5201
CV(0): A1( 3 )-> A1( 4 ) c_i: 0.9883 Per: 97.7% IPA: 10.736 eV Oai: 0.5163
CV(0): B1( 1 )-> B1( 2 ) c_i: -0.1265 Per: 1.6% IPA: 16.941 eV Oai: 0.6563
Estimate memory in tddft_init mem: 0.001 M
其中第1行的信息,
No. 1 w= 9.3784 eV表示第一激发态激发能为9.3784 eV;-76.0358398606 a.u.给出第一激发态的总能量;f= 0.0767给出第一激发态与基态之间跃迁的振子强度;D<Pab>= 0.0000为激发态的<S^2>值与基态的<S^2>值之差(对于自旋守恒跃迁,该值反映了激发态的自旋污染程度;对于自旋翻转跃迁,该值与理论值S(S+1)(激发态)-S(S+1)(基态)之差反映了激发态的自旋污染程度);Ova= 0.5201为绝对重叠积分(absolute overlap integral,取值范围为[0,1],该值越接近0,说明相应的激发态的电荷转移特征越明显,否则说明局域激发特征越明显)。
第2行和第3行给出激发主组态信息
CV(0):中CV(0)表示该激发是Core到Virtual轨道激发,0表示是Singlet激发;A1( 3 )-> A1( 4 )给出了电子跃迁的占据-空轨道对,电子从A1表示的第3个轨道跃迁到A1表示的第4个轨道,结合上面输出轨道信息,可看出这是HOMO-2到LUMO的激发;c_i: 0.9883表示该跃迁在整个激发态里的线性组合系数为0.9883;Per: 97.7%表示该激发组态占97.7%;IPA: 10.736 eV代表该跃迁所涉及的两个轨道的能量差为10.736 eV;Oai: 0.5163表示假如该激发态只有这一个跃迁的贡献,那么该激发态的绝对重叠积分为0.5001,由这一信息可以方便地得知哪些跃迁是局域激发,哪些跃迁是电荷转移激发。
所有不可约表示求解完后,所有的激发态会按照能量高低排列总结输出,并打印对应的振子强度等信息,
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 B2 1 B2 7.1935 eV 172.36 nm 0.0188 0.0000 99.8% CV(0): B2( 1 )-> A1( 4 ) 8.853 0.426 0.0000
2 A2 1 A2 9.0191 eV 137.47 nm 0.0000 0.0000 99.8% CV(0): B2( 1 )-> B1( 2 ) 10.897 0.356 1.8256
3 A1 2 A1 9.3784 eV 132.20 nm 0.0767 0.0000 97.7% CV(0): A1( 3 )-> A1( 4 ) 10.736 0.520 2.1850
4 B1 1 B1 11.2755 eV 109.96 nm 0.0631 0.0000 98.0% CV(0): A1( 3 )-> B1( 2 ) 12.779 0.473 4.0820
随后还打印了跃迁偶极矩。
*** Ground to excited state Transition electric dipole moments (Au) ***
State X Y Z Osc.
1 -0.0000 -0.3266 0.0000 0.0188 0.0188
2 0.0000 0.0000 0.0000 0.0000 0.0000
3 0.0000 0.0000 0.5777 0.0767 0.0767
4 0.4778 -0.0000 0.0000 0.0631 0.0631
开壳层体系计算:U-TDDFT
开壳层体系可以用U-TDDFT计算,例如对于 \(\ce{H2O+}\) 离子,先进行UKS计算,然后利用U-TDDFT计算激发态。典型的输入为,
#!bdf.sh
TDDFT/B3lyp/cc-pvdz iroot=4 group=C(1) charge=1
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
这里,关键词
iroot=4指定对每个不可约表示计算4个根;charge=1指定体系的电荷为+1;group=C(1)指定强制使用C1点群计算。
与之对应的高级输入为,
$compass
#Notice: The unit of molecular coordinate is angstrom
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
basis
cc-pVDZ
group
C(1) # Force to use C1 symmetry
$end
$xuanyuan
$end
$scf
uks
dft
b3lyp
charge
1
spinmulti
2
$end
$tddft
iroot
4
$end
这个输入要注意的几个细节是:
compass模块中利用关键词group强制计算使用C(1)点群;scf模块设置UKS计算,charge为1,spinmulti(自旋多重度,2S+1)=2;tddft模块的iroot设定每个不可约表示算4个根,由于用了C1对称性,计算给出水的阳离子的前四个激发态。
从以下输出可以看出执行的是U-TDDFT计算:
--------------------------------------------------
--- PRINT: Information about TDDFT calculation ---
--------------------------------------------------
ERI Maxblk= 8M
[print level]
iprt= 0
[method]
U-TD-DFT
isf= 0
SC Excitations
RPA: (A-B)(A+B)Z=w2*Z
计算总结输出的4个激发态为,
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 2 A 2.1960 eV 564.60 nm 0.0009 0.0024 99.4% CO(bb): A( 4 )-> A( 5 ) 5.955 0.626 0.0000
2 A 3 A 6.3479 eV 195.31 nm 0.0000 0.0030 99.3% CO(bb): A( 3 )-> A( 5 ) 9.983 0.578 4.1520
3 A 4 A 12.0991 eV 102.47 nm 0.0028 1.9312 65.8% CV(bb): A( 4 )-> A( 6 ) 14.637 0.493 9.9032
4 A 5 A 13.3618 eV 92.79 nm 0.0174 0.0004 97.6% CV(aa): A( 4 )-> A( 6 ) 15.624 0.419 11.1659
其中第3激发态的 D<S^2> 值较大,表明存在自旋污染问题。
开壳层体系:X-TDDFT(也称SA-TDDFT)
X-TDDFT是一种自旋匹配TDDFT方法,用于计算开壳层体系。 开壳层体系U-TDDFT三重态耦合的双占据到虚轨道激发态(在BDF中标记为CV(1))存在自旋污染问题,因而其激发能常被低估。X-TDDFT可以用于解决这一问题。考虑 \(\ce{N2+}\) 分子,X-TDDFT的简洁计算输入为:
#! N2+.sh
X-TDDFT/b3lyp/aug-cc-pvtz group=D(2h) charge=1 spinmulti=2 iroot=5
Geometry
N 0.00 0.00 0.00
N 0.00 0.00 1.1164
End geometry
高级输入:
$compass
#Notice: The unit of molecular coordinate is angstrom
Geometry
N 0.00 0.00 0.00
N 0.00 0.00 1.1164
End geometry
basis
aug-cc-pvtz
group
D(2h) # Force to use D2h symmetry
$end
$xuanyuan
$end
$scf
roks # ask for ROKS calculation
dft
b3lyp
charge
1
spinmulti
2
$end
$tddft
iroot
5
$end
这里, SCF 模块要求用 ROKS 方法计算基态, TDDFT 模块将默认采用 X-TDDFT 计算。
激发态输出为,
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 B2u 1 B2u 0.7902 eV 1569.00 nm 0.0017 0.0195 98.6% CO(0): B2u( 1 )-> Ag( 3 ) 3.812 0.605 0.0000
2 B3u 1 B3u 0.7902 eV 1569.00 nm 0.0017 0.0195 98.6% CO(0): B3u( 1 )-> Ag( 3 ) 3.812 0.605 0.0000
3 B1u 1 B1u 3.2165 eV 385.46 nm 0.0378 0.3137 82.6% CO(0): B1u( 2 )-> Ag( 3 ) 5.487 0.897 2.4263
4 B1u 2 B1u 8.2479 eV 150.32 nm 0.0008 0.9514 48.9% CV(1): B2u( 1 )-> B3g( 1 ) 12.415 0.903 7.4577
5 Au 1 Au 8.9450 eV 138.61 nm 0.0000 1.2618 49.1% CV(0): B2u( 1 )-> B2g( 1 ) 12.903 0.574 8.1548
6 Au 2 Au 9.0519 eV 136.97 nm 0.0000 1.7806 40.1% CV(1): B3u( 1 )-> B3g( 1 ) 12.415 0.573 8.2617
7 B1u 3 B1u 9.0519 eV 136.97 nm 0.0000 1.7806 40.1% CV(1): B3u( 1 )-> B2g( 1 ) 12.415 0.906 8.2617
8 B2g 1 B2g 9.4442 eV 131.28 nm 0.0000 0.0061 99.0% OV(0): Ag( 3 )-> B2g( 1 ) 12.174 0.683 8.6540
9 B3g 1 B3g 9.4442 eV 131.28 nm 0.0000 0.0061 99.0% OV(0): Ag( 3 )-> B3g( 1 ) 12.174 0.683 8.6540
10 Au 3 Au 9.5281 eV 130.12 nm 0.0000 0.1268 37.0% CV(0): B3u( 1 )-> B3g( 1 ) 12.903 0.574 8.7379
11 B1u 4 B1u 9.5281 eV 130.12 nm 0.0000 0.1267 37.0% CV(0): B2u( 1 )-> B3g( 1 ) 12.903 0.909 8.7379
12 Au 4 Au 10.7557 eV 115.27 nm 0.0000 0.7378 49.1% CV(1): B3u( 1 )-> B3g( 1 ) 12.415 0.575 9.9655
13 B3u 2 B3u 12.4087 eV 99.92 nm 0.0983 0.1371 70.4% CV(0): B1u( 2 )-> B2g( 1 ) 15.288 0.793 11.6185
14 B2u 2 B2u 12.4087 eV 99.92 nm 0.0983 0.1371 70.4% CV(0): B1u( 2 )-> B3g( 1 ) 15.288 0.793 11.6185
15 B1u 5 B1u 15.9005 eV 77.98 nm 0.7766 0.7768 32.1% CV(0): B3u( 1 )-> B2g( 1 ) 12.903 0.742 15.1103
16 B2u 3 B2u 17.6494 eV 70.25 nm 0.1101 0.4841 92.0% CV(0): B2u( 1 )-> Ag( 4 ) 19.343 0.343 16.8592
17 B3u 3 B3u 17.6494 eV 70.25 nm 0.1101 0.4841 92.0% CV(0): B3u( 1 )-> Ag( 4 ) 19.343 0.343 16.8592
18 Ag 2 Ag 18.2820 eV 67.82 nm 0.0000 0.0132 85.2% OV(0): Ag( 3 )-> Ag( 4 ) 19.677 0.382 17.4918
19 B2u 4 B2u 18.5465 eV 66.85 nm 0.0021 1.5661 77.8% CV(1): B2u( 1 )-> Ag( 4 ) 19.825 0.401 17.7562
20 B3u 4 B3u 18.5465 eV 66.85 nm 0.0021 1.5661 77.8% CV(1): B3u( 1 )-> Ag( 4 ) 19.825 0.401 17.7562
21 Ag 3 Ag 18.7805 eV 66.02 nm 0.0000 0.2156 40.4% CV(0): B3u( 1 )-> B3u( 2 ) 20.243 0.337 17.9903
22 B1g 1 B1g 18.7892 eV 65.99 nm 0.0000 0.2191 40.5% CV(0): B2u( 1 )-> B3u( 2 ) 20.243 0.213 17.9990
23 B1g 2 B1g 18.8704 eV 65.70 nm 0.0000 0.2625 41.8% CV(0): B3u( 1 )-> B2u( 2 ) 20.243 0.213 18.0802
24 B3g 2 B3g 18.9955 eV 65.27 nm 0.0000 0.2673 83.4% CV(0): B2u( 1 )-> B1u( 3 ) 20.290 0.230 18.2053
25 B2g 2 B2g 18.9955 eV 65.27 nm 0.0000 0.2673 83.4% CV(0): B3u( 1 )-> B1u( 3 ) 20.290 0.230 18.2053
26 B3u 5 B3u 19.0339 eV 65.14 nm 0.0168 1.6012 66.7% CV(1): B1u( 2 )-> B2g( 1 ) 20.612 0.715 18.2437
27 B2u 5 B2u 19.0339 eV 65.14 nm 0.0168 1.6012 66.7% CV(1): B1u( 2 )-> B3g( 1 ) 20.612 0.715 18.2437
28 Ag 4 Ag 19.0387 eV 65.12 nm 0.0000 0.0693 35.9% CO(0): Ag( 2 )-> Ag( 3 ) 21.933 0.437 18.2484
29 Ag 5 Ag 19.3341 eV 64.13 nm 0.0000 0.1694 44.7% CO(0): Ag( 2 )-> Ag( 3 ) 21.933 0.457 18.5439
30 Ag 6 Ag 19.8685 eV 62.40 nm 0.0000 1.7807 40.4% CV(1): B3u( 1 )-> B3u( 2 ) 21.084 0.338 19.0783
31 B1g 3 B1g 19.8695 eV 62.40 nm 0.0000 1.7774 40.5% CV(1): B2u( 1 )-> B3u( 2 ) 21.084 0.213 19.0792
32 B3g 3 B3g 19.9858 eV 62.04 nm 0.0000 1.6935 80.7% CV(1): B2u( 1 )-> B1u( 3 ) 21.038 0.231 19.1956
33 B2g 3 B2g 19.9858 eV 62.04 nm 0.0000 1.6935 80.7% CV(1): B3u( 1 )-> B1u( 3 ) 21.038 0.231 19.1956
34 B1g 4 B1g 19.9988 eV 62.00 nm 0.0000 1.7373 41.8% CV(1): B3u( 1 )-> B2u( 2 ) 21.084 0.213 19.2086
35 B2g 4 B2g 20.2417 eV 61.25 nm 0.0000 0.2901 81.4% CV(0): B1u( 2 )-> B3u( 2 ) 22.628 0.228 19.4515
36 B3g 4 B3g 20.2417 eV 61.25 nm 0.0000 0.2901 81.4% CV(0): B1u( 2 )-> B2u( 2 ) 22.628 0.228 19.4515
37 Au 5 Au 21.2302 eV 58.40 nm 0.0000 0.2173 40.4% CV(0): B2u( 1 )-> B2g( 2 ) 22.471 0.157 20.4400
38 B2g 5 B2g 22.1001 eV 56.10 nm 0.0000 0.0031 99.2% OV(0): Ag( 3 )-> B2g( 2 ) 23.220 0.204 21.3099
39 B3g 5 B3g 22.1001 eV 56.10 nm 0.0000 0.0031 99.2% OV(0): Ag( 3 )-> B3g( 2 ) 23.220 0.204 21.3099
40 B1g 5 B1g 23.4663 eV 52.84 nm 0.0000 0.0027 99.8% OV(0): Ag( 3 )-> B1g( 1 ) 25.135 0.283 22.6761
这里,第4、6、7激发态都是CV(1)态。注意SA-TDDFT计算的 D<S^2> 值是按U-TDDFT的公式计算出来的,可以近似地表明假如用U-TDDFT计算这些态的话,结果的自旋污染程度,但并不代表这些态实际的自旋污染程度,因为SA-TDDFT可以保证所有激发态都严格不存在自旋污染。因此如果SA-TDDFT算得的某个态的 D<S^2> 值很大,并不能表明该态的结果不可靠,相反表示对于该态而言SA-TDDFT相比U-TDDFT的改进比较大。
以闭壳层单重态为参考态计算三重态激发态
从 \(\ce{H2O}\) 分子闭壳层的基态出发,可以计算三重激发态。简洁输入为:
#! bdf.sh
tdft/b3lyp/cc-pvdz iroot=4 spinflip=1
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
注意这里虽然关键词名为spinflip,但该计算并不是一个自旋翻转TDDFT计算,因为其计算的是三重态激发态的 \(M_S = 0\) 组分而非 \(M_S = 1\) 组分。对应的高级输入为:
$compass
#Notice: Coordinate unit is angstrom
geometry
O
H 1 R1
H 1 R1 2 109.
R1=1.0 # OH bond length in angstrom
end geometry
basis
cc-pvdz
group
C(1) # Force to use C1 symmetry
$end
$xuanyuan
$end
$scf
rks # ask for RKS calculation
dft
b3lyp
$end
$tddft
isf # ask for triplet TDDFT calculation
1
iroot
4
$end
TDDFT计算快结束时有输出信息如下,
*** List of excitations ***
Ground-state spatial symmetry: A
Ground-state spin: Si= 0.0000
Spin change: isf= 1
D<S^2>_pure= 2.0000 for excited state (Sf=Si+1)
D<S^2>_pure= 0.0000 for excited state (Sf=Si)
Imaginary/complex excitation energies : 0 states
Reversed sign excitation energies : 0 states
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 1 A 6.4131 eV 193.33 nm 0.0000 2.0000 99.2% CV(1): A( 5 )-> A( 6 ) 8.853 0.426 0.0000
2 A 2 A 8.2309 eV 150.63 nm 0.0000 2.0000 97.7% CV(1): A( 4 )-> A( 6 ) 10.736 0.519 1.8177
3 A 3 A 8.4793 eV 146.22 nm 0.0000 2.0000 98.9% CV(1): A( 5 )-> A( 7 ) 10.897 0.357 2.0661
4 A 4 A 10.1315 eV 122.37 nm 0.0000 2.0000 92.8% CV(1): A( 4 )-> A( 7 ) 12.779 0.479 3.7184
*** Ground to excited state Transition electric dipole moments (Au) ***
State X Y Z Osc.
1 0.0000 0.0000 0.0000 0.0000 0.0000
2 0.0000 0.0000 0.0000 0.0000 0.0000
3 0.0000 0.0000 0.0000 0.0000 0.0000
4 0.0000 0.0000 0.0000 0.0000 0.0000
其中, Spin change: isf= 1 提示计算的是自旋多重度比基态大2的态(也即三重态),由于基态是单重态,基态到激发态跃迁是自旋禁阻的,所以振子强度和跃迁偶极矩都是0.
TDDFT 默认只计算与参考态自旋相同的激发态, 例如,\(\ce{H2O}\) 分子的基态是单重态,TDDFT值计算单重激发态,如果要同时计算单重态与三重态,输入为:
#! H2OTDDFT.sh
TDDFT/b3lyp/cc-pVDZ iroot=4 spinflip=0,1
geometry
O
H 1 0.9
H 1 0.9 2 109.0
end geometry
系统会运行两次TDDFT,分别计算单重态和三重态,其中单重态的输出为:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 B2 1 B2 8.0968 eV 153.13 nm 0.0292 0.0000 99.9% CV(0): B2( 1 )-> A1( 4 ) 9.705 0.415 0.0000
2 A2 1 A2 9.9625 eV 124.45 nm 0.0000 0.0000 99.9% CV(0): B2( 1 )-> B1( 2 ) 11.745 0.329 1.8656
3 A1 2 A1 10.1059 eV 122.69 nm 0.0711 0.0000 99.1% CV(0): A1( 3 )-> A1( 4 ) 11.578 0.442 2.0090
4 B1 1 B1 12.0826 eV 102.61 nm 0.0421 0.0000 99.5% CV(0): A1( 3 )-> B1( 2 ) 13.618 0.392 3.9857
5 B1 2 B1 15.1845 eV 81.65 nm 0.2475 0.0000 99.5% CV(0): B1( 1 )-> A1( 4 ) 16.602 0.519 7.0877
6 A1 3 A1 17.9209 eV 69.18 nm 0.0843 0.0000 95.4% CV(0): B1( 1 )-> B1( 2 ) 18.643 0.585 9.8240
7 A2 2 A2 22.3252 eV 55.54 nm 0.0000 0.0000 99.8% CV(0): B2( 1 )-> B1( 3 ) 24.716 0.418 14.2284
...
三重态的输出为:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 B2 1 B2 7.4183 eV 167.13 nm 0.0000 2.0000 99.4% CV(1): B2( 1 )-> A1( 4 ) 9.705 0.415 0.0000
2 A1 1 A1 9.3311 eV 132.87 nm 0.0000 2.0000 98.9% CV(1): A1( 3 )-> A1( 4 ) 11.578 0.441 1.9128
3 A2 1 A2 9.5545 eV 129.76 nm 0.0000 2.0000 99.2% CV(1): B2( 1 )-> B1( 2 ) 11.745 0.330 2.1363
4 B1 1 B1 11.3278 eV 109.45 nm 0.0000 2.0000 97.5% CV(1): A1( 3 )-> B1( 2 ) 13.618 0.395 3.9095
5 B1 2 B1 14.0894 eV 88.00 nm 0.0000 2.0000 97.8% CV(1): B1( 1 )-> A1( 4 ) 16.602 0.520 6.6711
6 A1 2 A1 15.8648 eV 78.15 nm 0.0000 2.0000 96.8% CV(1): B1( 1 )-> B1( 2 ) 18.643 0.582 8.4465
7 A2 2 A2 21.8438 eV 56.76 nm 0.0000 2.0000 99.5% CV(1): B2( 1 )-> B1( 3 ) 24.716 0.418 14.4255
...
由于单重态到三重态跃迁是偶极禁阻的,所以振子强度 f=0.0000。
自旋翻转 (spin-flip) TDDFT计算
BDF不仅能从单重态出发计算三重态,还可以从自旋多重度更高的 2S+1 重态(S = 1/2, 1, 3/2, …)出发,向上翻转自旋计算 2S+3 重态;自旋上翻的 TDDFT/TDA 给出的是双占据轨道的alpha电子到未占据的beta轨道跃迁态,标记为 CV(1) 激发。与基态为闭壳层单重态的情形不同,此时BDF计算的是 2S+3 重态的 \(M_S = S+1\) 组分,因此当基态不是闭壳层单重态时,该计算可以称之为自旋翻转的TDDFT计算。自旋向上翻转的TDDFT计算的输入文件格式与基态为闭壳层单重态、计算三重态激发态时完全相同,例如以下输入文件以二重态为参考态,计算四重态激发态:
...
$scf
UKS
...
spinmulti
2
$end
$tddft
...
isf
1
$end
此外,BDF还可以从三重态出发,向下翻转自旋计算单重态,这时需要设置 isf 为 -1。当然,也可以从自旋多重度更高的态向下翻转计算自旋多重度少2的态。要注意的是,自旋下翻的 TDDFT/TDA 只能正确描述从开壳层占据的alpha轨道到开壳层占据的beta轨道跃迁的电子态,标记为 OO(ab) 跃迁,其它跃迁类型的态都有自旋污染问题。
从三重态出发,向下反转自旋计算单重态,输入为:
#! H2OTDDFT.sh
TDA/b3lyp/cc-pVDZ spinmulti=3 iroot=-4 spinflip=-1
geometry
O
H 1 0.9
H 1 0.9 2 109.0
end geometry
输出为:
Imaginary/complex excitation energies : 0 states
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 1 A -8.6059 eV -144.07 nm 0.0000 -1.9933 99.3% OO(ab): A( 6 )-> A( 5 ) -6.123 0.408 0.0000
2 A 2 A -0.0311 eV -39809.08 nm 0.0000 -0.0034 54.1% OO(ab): A( 5 )-> A( 5 ) 7.331 1.000 8.5747
3 A 3 A 0.5166 eV 2399.85 nm 0.0000 -1.9935 54.0% OO(ab): A( 6 )-> A( 6 ) 2.712 0.999 9.1225
4 A 4 A 2.3121 eV 536.24 nm 0.0000 -0.9994 99.9% OV(ab): A( 6 )-> A( 7 ) 4.671 0.872 10.9180
这里,前三个态都是 OO(ab) 类型的激发态,其中第1个态和第3个态基本是纯的单重态(D<S^2>约等于-2,即激发态的<S^2>约等于0),第2个态基本是纯的三重态(D<S^2>约等于0);第四个态是 OV(ab) 类型的激发态,有自旋污染问题(D<S^2>约等于-1,即激发态的<S^2>约等于1,介于单重态和三重态之间),其激发能不可靠。
警告
BDF目前只支持自旋翻转的TDA,而不支持自旋翻转的TDDFT。但以闭壳层单重态为参考态计算三重态激发态不受此限制。
用iVI方法计算UV-Vis和XAS光谱
以上各算例是基于Davidson方法求解的TDDFT激发态。为了用Davidson方法求出某一个激发态,一般需要同时求解比它能量更低的所有激发态,因此当目标激发态的能量很高时(例如在计算XAS光谱时),Davidson方法需要的计算资源过多,在有限的计算时间和内存的限制下无法求得结果。此外,用户使用Davidson方法时,必须在计算之前就指定求解的激发态数目,然而很多时候用户在计算之前并不知道自己需要的激发态是第几个激发态,而只知道自己需要的激发态的大致能量范围等信息,这就使得用户必须经过一系列试错,先设定较少的激发态数目进行计算,如果发现没有算出自己需要的态,再增加激发态的数目、重算,直至找到自己需要的态为止。显然这样会无端消耗用户的精力以及机时。
BDF的iVI方法为以上问题提供了一种解决方案。在iVI方法中,用户可以指定感兴趣的激发能范围(比如整个可见区,或者碳的K-edge区域),而无需估计该范围内有多少个激发态;程序可以计算出激发能处于该范围内的所有激发态,一方面无需像Davidson方法那样计算比该范围的能量更低的激发态,另一方面可以确保得到该能量范围内的所有激发态,没有遗漏。以下举两个算例:
(1)计算DDQ自由基阴离子在400-700 nm范围内的吸收光谱(X-TDDFT,wB97X/LANL2DZ)
$COMPASS
Title
DDQ radical anion TDDFT
Basis
LANL2DZ
Geometry # UB3LYP/def2-SVP geometry
C 0.00000000 2.81252550 -0.25536084
C 0.00000000 1.32952185 -2.58630187
C 0.00000000 -1.32952185 -2.58630187
C 0.00000000 -2.81252550 -0.25536084
C 0.00000000 -1.29206304 2.09336443
C -0.00000000 1.29206304 2.09336443
Cl 0.00000000 -3.02272954 4.89063172
Cl -0.00000000 3.02272954 4.89063172
C 0.00000000 -2.72722649 -4.89578100
C -0.00000000 2.72722649 -4.89578100
N 0.00000000 -3.86127688 -6.78015122
N -0.00000000 3.86127688 -6.78015122
O 0.00000000 -5.15052650 -0.22779097
O -0.00000000 5.15052650 -0.22779097
End geometry
units
bohr
mpec+cosx # accelerate the calculation (both the SCF and TDDFT parts) using MPEC+COSX
$end
$XUANYUAN
rs
0.3 # rs for wB97X
$END
$SCF
roks
dft
wB97X
charge
-1
$END
$tddft
iprt # print level
2
itda
0
idiag # selects the iVI method
3
iwindow
400 700 nm # alternatively the unit can be given as au, eV or cm-1 instead of nm.
# default is in eV if no unit is given
itest
1
icorrect
1
memjkop
2048
$end
因该分子属于 \(\rm C_{2v}\) 点群,共有4个不可约表示(A1,A2,B1,B2),程序分别在4个不可约表示下求解TDDFT问题。以A1不可约表示为例,iVI迭代收敛后,程序输出如下信息:
Root 0, E= 0.1060649560, residual= 0.0002136455
Root 1, E= 0.1827715245, residual= 0.0005375061
Root 2, E= 0.1863919913, residual= 0.0006792424
Root 3, E= 0.2039707800, residual= 0.0008796108
Root 4, E= 0.2188244775, residual= 0.0015619745
Root 5, E= 0.2299349293, residual= 0.0010684879
Root 6, E= 0.2388141752, residual= 0.0618579646
Root 7, E= 0.2609321083, residual= 0.0695001907
Root 8, E= 0.2649984329, residual= 0.0759920121
Root 9, E= 0.2657352154, residual= 0.0548521587
Root 10, E= 0.2743644891, residual= 0.0655238098
Root 11, E= 0.2766959875, residual= 0.0600950472
Root 12, E= 0.2803090818, residual= 0.0587604503
Root 13, E= 0.2958382984, residual= 0.0715968457
Root 14, E= 0.3002756135, residual= 0.0607394762
Root 15, E= 0.3069930238, residual= 0.0720773993
Root 16, E= 0.3099721369, residual= 0.0956453409
Root 17, E= 0.3141986951, residual= 0.0688103843
Excitation energies of roots within the energy window (au):
0.1060649560
Timing Spin analyze : 0.01 0.00 0.00
No. 1 w= 2.8862 eV -594.3472248862 a.u. f= 0.0000 D<Pab>= 0.0717 Ova= 0.5262
CO(bb): A1( 20 )-> A2( 4 ) c_i: -0.9623 Per: 92.6% IPA: 8.586 eV Oai: 0.5360
CV(bb): A1( 20 )-> A2( 5 ) c_i: -0.1121 Per: 1.3% IPA: 11.748 eV Oai: 0.3581
CV(bb): B1( 18 )-> B2( 6 ) c_i: 0.2040 Per: 4.2% IPA: 13.866 eV Oai: 0.4328
可以看到程序在此不可约表示下计算出了17个激发态,但其中只有一个激发态(激发能0.106 au = 2.89 eV)在用户指定的波长区间(400-700 nm)内,因而完全收敛(表现为残差 (residual) 很小);其余激发态在远未收敛之前,程序即知道其不在用户感兴趣的范围内,因而不再尝试收敛这些激发态(表现为残差很大),由此节省了很多计算量。
所有4个不可约表示均计算完成后,程序照常将各不可约表示的计算结果汇总:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A1 2 A2 2.4184 eV 512.66 nm 0.1339 0.0280 93.0% OV(aa): A2( 4 )-> A2( 5 ) 7.064 0.781 0.0000
2 B2 1 B1 2.7725 eV 447.19 nm 0.0000 0.0000 92.5% CO(bb): B1( 18 )-> A2( 4 ) 8.394 0.543 0.3541
3 A2 1 A1 2.8862 eV 429.58 nm 0.0000 0.0000 92.6% CO(bb): A1( 20 )-> A2( 4 ) 8.586 0.526 0.4677
4 B1 1 B2 3.0126 eV 411.55 nm 0.0000 0.0000 63.5% CO(bb): B2( 4 )-> A2( 4 ) 8.195 0.820 0.5942
(2)计算乙烯的碳K-edge XAS光谱(sf-X2C,M06-2X/uncontracted def2-TZVP)
$COMPASS
Title
iVI test
Basis
def2-TZVP
geometry
C -5.77123022 1.49913343 0.00000000
H -5.23806647 0.57142851 0.00000000
H -6.84123022 1.49913343 0.00000000
C -5.09595591 2.67411072 0.00000000
H -5.62911966 3.60181564 0.00000000
H -4.02595591 2.67411072 0.00000000
End geometry
group
c(1)
uncontract # uncontract the basis set (beneficial for the accuracy of core excitations)
$END
$XUANYUAN
heff
3 # selects sf-X2C
$END
$SCF
rks
dft
m062x
$END
$TDDFT
imethod
1 # R-TDDFT
idiag
3 # iVI
iwindow
275 285 # default unit: eV
$end
由实验得知碳的K-edge吸收在280 eV附近,因此这里的能量范围选为275-285 eV。计算得到该能量区间内共有15个激发态:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 2 A 277.1304 eV 4.47 nm 0.0018 0.0000 97.1% CV(0): A( 5 )-> A( 93 ) 281.033 0.650 0.0000
2 A 3 A 277.1998 eV 4.47 nm 0.0002 0.0000 96.0% CV(0): A( 6 )-> A( 94 ) 282.498 0.541 0.0694
3 A 4 A 277.9273 eV 4.46 nm 0.0045 0.0000 92.8% CV(0): A( 7 )-> A( 94 ) 281.169 0.701 0.7969
4 A 5 A 278.2593 eV 4.46 nm 0.0000 0.0000 100.0% CV(0): A( 8 )-> A( 95 ) 283.154 0.250 1.1289
5 A 6 A 279.2552 eV 4.44 nm 0.0002 0.0000 85.5% CV(0): A( 4 )-> A( 93 ) 284.265 0.627 2.1247
6 A 7 A 280.0107 eV 4.43 nm 0.0000 0.0000 96.6% CV(0): A( 8 )-> A( 96 ) 284.941 0.315 2.8803
7 A 8 A 280.5671 eV 4.42 nm 0.0000 0.0000 97.0% CV(0): A( 5 )-> A( 94 ) 284.433 0.642 3.4366
8 A 9 A 280.8642 eV 4.41 nm 0.1133 0.0000 93.3% CV(0): A( 2 )-> A( 9 ) 287.856 0.179 3.7337
9 A 10 A 280.8973 eV 4.41 nm 0.0000 0.0000 90.1% CV(0): A( 1 )-> A( 9 ) 287.884 0.185 3.7668
10 A 11 A 281.0807 eV 4.41 nm 0.0000 0.0000 66.8% CV(0): A( 6 )-> A( 95 ) 287.143 0.564 3.9502
11 A 12 A 282.6241 eV 4.39 nm 0.0000 0.0000 97.7% CV(0): A( 7 )-> A( 95 ) 285.815 0.709 5.4937
12 A 13 A 283.7528 eV 4.37 nm 0.0000 0.0000 65.1% CV(0): A( 4 )-> A( 94 ) 287.666 0.592 6.6223
13 A 14 A 283.9776 eV 4.37 nm 0.0000 0.0000 92.1% CV(0): A( 6 )-> A( 96 ) 288.929 0.523 6.8471
14 A 15 A 284.1224 eV 4.36 nm 0.0008 0.0000 98.2% CV(0): A( 7 )-> A( 96 ) 287.601 0.707 6.9920
15 A 16 A 284.4174 eV 4.36 nm 0.0000 0.0000 93.7% CV(0): A( 3 )-> A( 93 ) 289.434 0.509 7.2869
但由激发态成分可以看出,只有激发能为280.8642 eV和280.8973 eV的两个激发态为C 1s到价层轨道的激发,其余激发均为价层轨道到非常高的Rydberg轨道的激发,也即对应于价层电子电离的背景吸收。
此外,即使用户没有不重不漏地计算某能量区间内所有激发态的需求,iVI相比Davidson方法仍有另一优势,即所需内存较少。Davidson方法所需内存随迭代次数的增加而线性增加,虽然BDF采取分批计算激发态、以及每几十步迭代重新构建Krylov子空间的方法减少内存消耗,但这会导致迭代次数增加,从而增加计算时间。而iVI方法因为每步迭代时都重新构建Krylov子空间,算法消耗的内存并不随迭代的进行而增加,相比Davidson方法可以节省2~10倍的内存消耗。因此,当Davidson方法所需内存超过当前节点的可用物理内存,但超过的比例在10倍以内时,改用iVI方法有一定概率可以让计算在给定的内存限制下正常完成。例如以下写法
$TDDFT
idiag
3 # iVI
iroot
-100
$end
即为用iVI方法计算能量最低的100个自旋守恒激发态。当内存足够时,计算时间与Davidson方法相差不多;当内存不能满足Davidson方法的需求,但差距不太远时,Davidson方法会因内存不足而报错退出,或因频繁重新构建Krylov子空间而导致迭代次数变多(甚至不收敛),而iVI方法仍可正常收敛。
快速近似计算大体系吸收光谱的方法:sTDA、sTDDFT
传统的TDDFT方法在计算大体系(例如数百个原子)的吸收光谱时,常常会遇到严重的CPU和内存瓶颈,导致计算无法在给定的计算时间和内存限制下完成。这不仅是因为计算每个激发态所需的计算资源变多,更是因为体系越大,其在一定波长范围(如可见光区)内的激发态数目就越多。因此,如果要计算某给定波长范围内的吸收光谱,则TDDFT计算所需时间和内存消耗不仅随体系大小快速增加,其与SCF步骤所需时间和内存的比值也是随体系大小的增加而增加的。也就是说,当体系足够大时,即使只对TDDFT步骤做近似,而不对SCF步骤做近似,也可以获得极大的加速,并节省大量内存。如上所述,iVI方法可以在一定程度上减少TDDFT计算所需内存,且不引入任何误差;而 MPEC+COSX方法 则可将TDDFT的计算时间降低至原来的1/10~1/3左右(视基组大小和体系大小而定),代价是引入极小(一般小于0.01 eV)的误差。但如果对结果精度的要求更低,例如即使0.2 eV量级的误差也可以接受,则可以利用Grimme课题组发展的sTDA、sTDDFT方法 [67, 68, 69] 加速TDDFT计算,可较普通TDDFT快数十至数百倍。在BDF里,可用 grimmestd 关键词来指定使用sTDA或sTDDFT方法。
例如,以下算例用sTDDFT计算叶绿素a(137个原子)的吸收光谱:
$compass
title
chlorophyll a
basis
def2-sv(p)
geometry
Mg -6.39280500 1.01913900 0.07930600
C -4.66061700 -1.97549200 0.32240100
C -3.86800400 2.56481900 1.82052600
C -8.08215800 3.98978800 -0.18167200
C -8.98545300 -0.61768600 -1.64547000
N -4.54433200 0.38436500 0.90884900
C -3.99700200 -0.93553500 0.86684800
C -3.70478200 1.19580500 1.58959100
N -6.02943300 2.90039700 0.68978700
C -4.94074100 3.33410600 1.39121000
C -5.07491500 4.81749500 1.63863600
C -6.24086300 5.22118200 1.06806800
C -6.89203100 4.01489100 0.45469200
C -4.06725100 5.61005500 2.36565900
C -6.80943200 6.56357900 1.03550500
C -7.16536900 7.19003700 -0.08627800
N -8.20213100 1.58193300 -0.75743000
C -8.71213700 2.83175300 -0.76290000
C -10.01431500 2.85490100 -1.44851000
C -10.27039900 1.56409200 -1.85400400
C -9.13329500 0.73615200 -1.42942600
C -10.84075600 4.06541800 -1.63406700
N -6.79660200 -0.84366300 -0.52933900
C -7.89913200 -1.40200500 -1.24381700
C -7.66635200 -2.82277100 -1.44961100
C -6.43617900 -3.10668000 -0.86460900
C -5.95222300 -1.85130000 -0.31154100
C -8.56834600 -3.75605800 -2.14493700
C -5.45761400 -4.14091100 -0.60755600
O -5.41067600 -5.29722700 -0.93531800
C -4.27700300 -3.43898300 0.19681800
C -4.03436300 -4.04185800 1.55541600
O -2.98821400 -4.06496400 2.17129100
O -5.18821800 -4.55887600 2.07822700
C -5.09043500 -5.21072200 3.37451000
H -3.08326400 3.06907300 2.38501100
H -8.64877900 4.92413800 -0.27855400
H -9.79244500 -1.13563000 -2.18571200
H -3.93018000 5.23884000 3.39358500
H -3.08555400 5.56125900 1.86717500
H -4.34148300 6.67290700 2.43393200
H -6.91464100 7.03432600 2.01872100
H -7.57843000 8.18875500 -0.09998800
H -7.06020700 6.75751400 -1.07293700
H -8.14333300 -4.77543300 -2.17957800
H -8.75310000 -3.45058300 -3.18537500
H -9.54347000 -3.83344900 -1.64123300
H -6.14095000 -5.40216500 3.61932300
H -4.61251400 -4.54263500 4.09691600
H -4.52176200 -6.13925800 3.26271900
H -11.76604400 3.85006500 -2.18728300
H -10.29928900 4.83683900 -2.20105400
H -11.13298700 4.50356100 -0.66841600
H -3.34289100 -3.55371300 -0.41277200
C -11.45722200 1.05206800 -2.59092400
H -11.76806300 0.06727900 -2.18361200
H -12.32721500 1.72374600 -2.42522700
C -11.17530300 0.93618900 -4.08970000
H -10.32963900 0.26795200 -4.29109700
H -12.04576500 0.54981100 -4.62999500
H -10.91967800 1.91226500 -4.52115700
C -2.62887700 -0.98246300 1.53480600
H -2.66523600 -1.73547400 2.36545400
C -2.45989500 0.45470900 2.10966600
H -1.54474300 0.93905400 1.69345300
C -1.51912600 -1.36887400 0.54488500
H -1.95440500 -1.82032400 -0.37473000
H -0.98048400 -0.46992100 0.18497700
C -0.53490800 -2.35906300 1.17264300
H -0.01435300 -1.91575300 2.04669100
H -1.09048500 -3.24472000 1.58712500
C 0.45366200 -2.85133200 0.15756500
O 0.32298700 -3.00078100 -1.03465600
O 1.62455500 -3.17223400 0.80990800
C 2.74348900 -3.67458400 0.01127500
H 3.16253400 -4.45724900 0.67208000
H 2.35407200 -4.12003600 -0.92533200
C -2.39399700 0.47145400 3.63155500
H -1.53316200 -0.10264900 3.99668600
H -2.29784400 1.49298200 4.01962300
H -3.29480800 0.03786900 4.08539800
C 3.69329800 -2.54884800 -0.22275100
H 3.47934900 -1.65803400 0.36902200
C 4.72857100 -2.60301500 -1.07403300
C 5.65017100 -1.42380300 -1.25339300
H 5.14884400 -0.48370900 -0.94555600
H 5.88443700 -1.28751700 -2.32864900
C 5.03510200 -3.81649000 -1.89435600
H 5.11655600 -4.71792300 -1.27224100
H 4.24043400 -3.99998600 -2.63355100
H 5.97637900 -3.72648800 -2.45109500
C 6.94460300 -1.61032500 -0.44635600
H 6.69651300 -1.73292300 0.62680900
H 7.44457000 -2.55070000 -0.74876300
C 7.89779300 -0.42393400 -0.63427700
H 7.40043300 0.51456700 -0.32490500
H 8.12487300 -0.30133700 -1.71103300
C 9.21414800 -0.60223000 0.15481900
H 9.61685800 -1.62347600 -0.05750700
C 8.97090200 -0.48135200 1.66411800
H 8.57313200 0.50305400 1.93258400
H 8.25269000 -1.23110800 2.01368400
H 9.89846400 -0.62443600 2.22911700
C 10.24945900 0.43890900 -0.32513700
H 10.24713000 0.48183100 -1.43148900
H 9.95072700 1.44860700 0.01380100
C 11.66689200 0.11913500 0.16783800
H 11.68178700 0.08831400 1.27533400
H 11.96235100 -0.89412300 -0.16596100
C 12.68264200 1.15206500 -0.33770400
H 12.39293700 2.16426800 0.00143900
H 12.65111300 1.18669100 -1.44390400
C 14.12108800 0.83574000 0.12861700
H 14.33172200 -0.24146100 -0.08434100
C 14.27459700 1.07059200 1.63652100
H 13.57809500 0.44876700 2.20914700
H 15.28809800 0.82990700 1.97526900
H 14.07897900 2.11411800 1.90509100
C 15.12505600 1.69543200 -0.67097600
H 14.85566900 1.67748900 -1.74474600
H 15.04336200 2.75380800 -0.36005400
C 16.57081500 1.21005300 -0.50195300
H 16.85440700 1.23936500 0.56866100
H 16.64949400 0.14854000 -0.80588000
C 17.54788100 2.06201800 -1.32247100
H 17.47406000 3.12251900 -1.01707800
H 17.25297400 2.03835700 -2.38919200
C 19.00728700 1.57806500 -1.18264700
H 19.02932300 0.46921900 -1.32861700
C 19.88192000 2.22132000 -2.26846200
H 19.87986900 3.31392300 -2.19414300
H 20.92289700 1.89145300 -2.18575500
H 19.53365000 1.95811100 -3.27242200
C 19.57038500 1.89281000 0.20940000
H 19.59163600 2.97072900 0.40174700
H 18.96496600 1.43221300 0.99745100
H 20.59391000 1.51998700 0.31823800
end geometry
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$tddft
iwindow
300 700 nm
grimmestd
$end
计算的SCF部分耗时527 s(16线程OpenMP并行,下同),TDDFT部分耗时仅152 s,得到以下的激发能和振子强度信息:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 2 A 2.1820 eV 568.22 nm 0.2526 0.0000 75.2% CV(0): A( 241 )-> A( 242 ) 2.473 0.725 0.0000
2 A 3 A 2.3886 eV 519.07 nm 0.0141 0.0000 60.8% CV(0): A( 240 )-> A( 242 ) 2.922 0.731 0.2066
3 A 4 A 3.0363 eV 408.34 nm 0.0101 0.0000 88.5% CV(0): A( 237 )-> A( 242 ) 3.896 0.368 0.8544
4 A 5 A 3.1122 eV 398.38 nm 0.0190 0.0000 92.1% CV(0): A( 239 )-> A( 242 ) 3.725 0.498 0.9302
5 A 6 A 3.1769 eV 390.27 nm 0.4325 0.0000 36.3% CV(0): A( 241 )-> A( 243 ) 3.179 0.662 0.9949
6 A 7 A 3.2453 eV 382.04 nm 0.0516 0.0000 86.5% CV(0): A( 236 )-> A( 242 ) 3.931 0.542 1.0634
7 A 8 A 3.2665 eV 379.57 nm 0.0007 0.0000 98.9% CV(0): A( 238 )-> A( 242 ) 3.748 0.030 1.0845
8 A 9 A 3.4194 eV 362.59 nm 0.6594 0.0000 50.2% CV(0): A( 240 )-> A( 243 ) 3.628 0.649 1.2375
9 A 10 A 3.5309 eV 351.14 nm 0.4136 0.0000 76.8% CV(0): A( 235 )-> A( 242 ) 4.125 0.577 1.3489
10 A 11 A 3.7388 eV 331.62 nm 0.0348 0.0000 93.3% CV(0): A( 239 )-> A( 243 ) 4.430 0.544 1.5568
11 A 12 A 3.7606 eV 329.69 nm 0.0599 0.0000 83.4% CV(0): A( 241 )-> A( 244 ) 4.229 0.648 1.5786
12 A 13 A 3.8813 eV 319.44 nm 0.0033 0.0000 94.2% CV(0): A( 237 )-> A( 243 ) 4.601 0.269 1.6993
13 A 14 A 3.9358 eV 315.01 nm 0.1686 0.0000 67.2% CV(0): A( 234 )-> A( 242 ) 4.532 0.633 1.7539
14 A 15 A 3.9750 eV 311.91 nm 0.0000 0.0000 99.7% CV(0): A( 238 )-> A( 243 ) 4.453 0.028 1.7930
15 A 16 A 4.0250 eV 308.04 nm 0.0187 0.0000 56.9% CV(0): A( 236 )-> A( 243 ) 4.636 0.512 1.8430
16 A 17 A 4.0346 eV 307.30 nm 0.0697 0.0000 32.9% CV(0): A( 233 )-> A( 242 ) 4.697 0.464 1.8526
17 A 18 A 4.0803 eV 303.86 nm 0.0461 0.0000 57.5% CV(0): A( 241 )-> A( 245 ) 4.702 0.492 1.8983
18 A 19 A 4.1011 eV 302.32 nm 0.0046 0.0000 49.1% CV(0): A( 233 )-> A( 242 ) 4.697 0.418 1.9192
相比之下,传统的TDDFT计算(与以上输入文件相同,区别仅在于去掉 grimmestd 关键字)耗时3264 s,结果为:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 2 A 2.2098 eV 561.08 nm 0.2224 0.0000 77.3% CV(0): A( 241 )-> A( 242 ) 2.473 0.724 0.0000
2 A 3 A 2.4379 eV 508.56 nm 0.0085 0.0000 60.0% CV(0): A( 240 )-> A( 242 ) 2.922 0.733 0.2282
3 A 4 A 3.1690 eV 391.24 nm 0.1398 0.0000 35.3% CV(0): A( 239 )-> A( 242 ) 3.725 0.490 0.9592
4 A 5 A 3.1923 eV 388.39 nm 0.0011 0.0000 49.7% CV(0): A( 239 )-> A( 242 ) 3.725 0.428 0.9825
5 A 6 A 3.2259 eV 384.34 nm 0.3826 0.0000 31.2% CV(0): A( 241 )-> A( 243 ) 3.179 0.608 1.0161
6 A 7 A 3.3241 eV 372.99 nm 0.0528 0.0000 88.4% CV(0): A( 236 )-> A( 242 ) 3.931 0.547 1.1143
7 A 8 A 3.4675 eV 357.56 nm 0.7779 0.0000 67.6% CV(0): A( 240 )-> A( 243 ) 3.628 0.667 1.2577
8 A 9 A 3.5022 eV 354.02 nm 0.0052 0.0000 99.4% CV(0): A( 238 )-> A( 242 ) 3.748 0.028 1.2925
9 A 10 A 3.5947 eV 344.91 nm 0.2244 0.0000 89.5% CV(0): A( 235 )-> A( 242 ) 4.125 0.561 1.3849
10 A 11 A 3.7945 eV 326.75 nm 0.0343 0.0000 88.7% CV(0): A( 239 )-> A( 243 ) 4.430 0.550 1.5847
11 A 12 A 3.8277 eV 323.92 nm 0.0463 0.0000 84.3% CV(0): A( 241 )-> A( 244 ) 4.229 0.648 1.6179
12 A 13 A 4.0449 eV 306.52 nm 0.0860 0.0000 72.5% CV(0): A( 234 )-> A( 242 ) 4.532 0.644 1.8351
13 A 14 A 4.0913 eV 303.04 nm 0.0021 0.0000 95.9% CV(0): A( 237 )-> A( 243 ) 4.601 0.264 1.8815
可以看到两个计算的激发能差别极小,在0.0~0.2 eV量级。表面上看,有一些态的振子强度差别很大,但这是因为激发能非常接近的态彼此之间混合的结果,如果作出光谱图(见 高斯展宽的吸收光谱的绘制 ),可以发现sTDDFT和TDDFT的吸收光谱基本相同,两者的差别在DFT计算的正常误差范围内:
与此同时,sTDDFT相比TDDFT节省了95 %的TDDFT计算时间(如包括SCF的计算时间,则节省了84 %的计算时间),可见加速效果十分可观。
除sTDDFT外,还可以将 grimmestd 关键字用于TDA计算,来指定进行sTDA计算,例如:
$tddft
itda
1
iwindow
300 700 nm
grimmestd
$end
当然,也可以指定计算的激发态数而非波长范围:
$tddft
nroot # calculate 100 lowest excited states per irrep
100
grimmestd
$end
更多注意事项请参见 grimmestd关键字的介绍 。
重启被意外中断的TDDFT任务
如TDDFT计算被意外终止,用户可能希望进行断点续算,即在重新做TDDFT计算的时候,利用之前的被中断的TDDFT任务产生的一些中间结果,来减少或避免重复计算。关于TDDFT计算断点续算的方法,详见 “常见问题”一章里的相应介绍 。
高斯展宽的吸收光谱的绘制
以上各计算得到的仅是各个激发态的激发能和振子强度,而用户常常需要得到理论预测的吸收谱的峰形,这就需要把每个激发态的吸收按一定的半峰宽进行高斯展宽。在BDF中,这是通过Python脚本plotspec.py(位于$BDFHOME/sbin/下,其中$BDFHOME是BDF的安装路径)来实现的。用户需要在TDDFT计算完成以后,手动从命令行调用plotspec.py。例如假设我们已经用BDF计算得到了C60分子的TDDFT激发态,对应的输出文件为C60.out,则可以运行
$BDFHOME/sbin/plotspec.py C60.out
或者
$BDFHOME/sbin/plotspec.py C60
该脚本会在屏幕上输出以下信息:
==================================
P L O T S P E C
Spectral broadening tool for BDF
==================================
BDF output file: C60.out
1 TDDFT output block(s) found
Block 1: 10 excited state(s)
- Singlet absorption spectrum, spin-allowed
The spectra will be Gaussian-broadened (FWHM = 0.5000 eV) ...
Absorption maxima of spectrum 1 (nm (lg epsilon/(L/(mol cm)))):
- 238 (5.12), 308 (4.50)
plotspec.py: exit successfully
并产生两个文件,一个是C60.stick.csv,包含所有激发态的吸收波长和摩尔消光系数,可以用来作棒状图:
TDDFT Singlets 1,,
Wavelength,Extinction coefficient,
nm,L/(mol cm),
342.867139,2899.779319,
307.302300,31192.802393,
237.635960,131840.430395,
211.765024,295.895849,
209.090150,134.498113,
197.019205,179194.526059,
178.561512,145.257962,
176.943322,54837.570677,
164.778366,548.752301,
160.167663,780.089056,
另一个是C60.spec.csv,包含高斯展宽后的吸收谱(默认的展宽FWHM为0.5 eV):
TDDFT Singlets 1,,
Wavelength,Extinction coefficient,
nm,L/(mol cm),
200.000000,162720.545118,
201.000000,151036.824457,
202.000000,137429.257570,
...
998.000000,0.000000,
999.000000,0.000000,
1000.000000,0.000000,
这两个文件可以用Excel、Origin等作图软件打开并作图:
可以用命令行参数控制作图范围、高斯展宽的FWHM等。示例:
# Plot the spectrum in the range 300-600 nm:
$BDFHOME/sbin/plotspec.py wavelength=300-600nm filename.out
# Plot an X-ray absorption spectrum in the range 200-210 eV,
# using an FWHM of 1 eV:
$BDFHOME/sbin/plotspec.py energy=200-210eV fwhm=1eV filename.out
# Plot a UV-Vis spectrum in the range 10000 cm-1 to 40000 cm-1,
# where the wavenumber is sampled at an interval of 50 cm-1:
$BDFHOME/sbin/plotspec.py wavenumber=10000-40000cm-1 interval=50 filename.out
# Plot an emission spectrum in the range 600-1200 nm, as would be
# given by Kasha's rule (i.e. only the first excited state is considered),
# where the wavelength is sampled at an interval of 5 nm:
$BDFHOME/sbin/plotspec.py -emi wavelength=600-1200nm interval=5 filename.out
如果不带命令行参数运行$BDFHOME/sbin/plotspec.py,可以列出所有的命令行参数及用法,这里不予赘述。
电子圆二色性(ECD)谱的计算
除吸收光谱外,BDF还支持在TDDFT级别下计算圆二色性(ECD)谱。用户只需在$tddft模块的输入中添加ECD关键字即可。例如以下输入文件在wB97X/ma-def2-TZVP水平下计算(S)-5-甲基环戊-2-烯-1-酮在160-300 nm范围内的ECD谱,溶剂为水:
$COMPASS
Title
ECD test
Basis
ma-def2-TZVP
Geometry # B3LYP/def2-SVP geometry
C 11.03017501307698 -1.06358915357097 18.65132535474617
C 12.57384005718525 -1.02456284484694 18.65658561738920
C 12.91529117412091 0.43177145174825 18.82255138315294
C 11.83078974644673 1.23189442235475 18.82242608164620
H 10.67388955940226 -1.47007769437446 19.61628109972719
H 13.00096293117676 -1.40629079282790 17.71067917782706
H 13.02306939327327 -1.63533989080155 19.45869631125239
H 13.94838829748073 0.77963695466942 18.91842719115154
H 11.81586135485978 2.32060314334658 18.90537981712256
C 10.61010494985639 0.41685642111484 18.65633627754937
O 9.46516754355473 0.82239910074197 18.54006339565965
C 10.37591484801120 -1.85714650215417 17.51891751829459
H 10.61141701850992 -2.93014535161767 17.59810807151853
H 9.28153845878811 -1.73962079399751 17.55678289237466
H 10.72376849425688 -1.50217177978463 16.53426564058783
End Geometry
MPEC+COSX
$END
$XUANYUAN
rs
0.3
$END
$SCF
RKS
DFT
wB97X
solvent
water
solmodel
SMD # IEFPCM is also a reasonable choice and is almost equally accurate
$END
$tddft
iprt
3
# To ensure that we get all roots within the window, we use the iVI method.
# Nevertheless, of course, iVI is not mandatory for ECD calculations
idiag
3 # use iVI
iwindow
160 300 nm
ecd # specifies ECD calculation
solneqlr # linear response solvation, recommended when the number of excited states
# is large
$end
该计算在输出吸收波长、振子强度、跃迁偶极矩后,还输出了跃迁磁偶极矩,以及长度、速度表象下的转子强度:
*** Ground to excited state Transition magnetic dipole moments (Au) ***
State X Y Z
1 -0.001936 0.002882 0.000034
2 -0.000444 -0.000188 -0.004692
3 -0.000342 -0.003475 -0.000070
4 -0.001232 0.000479 -0.001992
5 0.000581 0.002272 -0.001047
6 -0.001917 0.003593 -0.000178
7 0.002065 0.000206 -0.000823
*** Electronic circular dichroism (ECD) rotatory strengths (1e-40 cgs) ***
State Length formalism Velocity formalism
1 -2.9144 -3.0791
2 18.0007 17.5760
3 -25.1038 -25.1132
4 -7.2316 -7.0551
5 25.1323 24.4034
6 -14.9753 -14.2051
7 -30.6305 -30.8057
接下来,可以用plotspec.py读取该输出文件中的转子强度信息,进行高斯展宽,得到.spec.csv和.stick.csv文件,作ECD图(其中因为吸收波长略小于160 nm的激发态在高斯展宽后会对160 nm附近的图谱有一定影响,160 nm附近的ECD谱可能不可靠,因此作图时只作到180 nm):
$BDFHOME/sbin/plotspec.py -cd wavelength=180-300 filename.out
结果如下:
备注
虽然当基组趋于完备时,速度表象下的转子强度和长度表象下的转子强度严格相等,但当基组大小有限时,速度表象下的转子强度不依赖于分子的取向和中心位置,但长度表象下的转子强度是依赖于分子的取向和中心位置的。因此,起码当分子比较大、基组不太大的情况下,速度表象下的转子强度结果较为可靠。plotspec.py默认是用速度表象下的转子强度来绘制ECD图的,如需要用长度表象下的转子强度来绘制ECD图,应将plotspec.py的命令行参数中的-cd改为-cdl。
因BDF和其他程序确定分子标准取向以及分子坐标原点的方法不同,BDF计算出的长度表象下的转子强度可能与其他程序存在少许差别,这是正常现象,是由上述长度表象下的转子强度的理论缺陷所导致的,不代表计算结果错误。但速度表象下的转子强度理应和其他程序吻合较好。
对于柔性分子,单一构象的ECD计算结果不可靠,建议结合CREST、Molclus等软件进行构象搜索,对所有主要构象分别计算ECD谱后,进行Boltzmann加权平均。
激发态结构优化
BDF不仅支持TDDFT单点能(即给定分子结构下的激发能)的计算,还支持激发态的结构优化、数值频率等计算。为此需要在 $tddft 模块之后添加 $resp 模块用于计算TDDFT能量的梯度,并在 $compass 模块后添加 $bdfopt 模块,利用TDDFT梯度信息进行结构优化和频率计算(详见 结构优化与频率计算 )。
以下是在B3LYP/cc-pVDZ水平下优化丁二烯第一激发态结构的算例:
$COMPASS
Title
C4H6
Basis
CC-PVDZ
Geometry # Coordinates in Angstrom. The structure has C(2h) symmetry
C -1.85874726 -0.13257980 0.00000000
H -1.95342119 -1.19838319 0.00000000
H -2.73563916 0.48057645 0.00000000
C -0.63203020 0.44338226 0.00000000
H -0.53735627 1.50918564 0.00000000
C 0.63203020 -0.44338226 0.00000000
H 0.53735627 -1.50918564 0.00000000
C 1.85874726 0.13257980 0.00000000
H 1.95342119 1.19838319 0.00000000
H 2.73563916 -0.48057645 0.00000000
End Geometry
$END
$BDFOPT
solver
1
$END
$XUANYUAN
$END
$SCF
RKS
dft
B3lyp
$END
$TDDFT
nroot
# The ordering of irreps of the C(2h) group is: Ag, Au, Bg, Bu
# Thus the following line specifies the calculation of the 1Bu state, which
# happens to be the first excited state for this particular molecule.
0 0 0 1
istore
1
# TDDFT gradient requires tighter TDDFT convergence criteria than single-point
# TDDFT calculations, thus we tighten the convergence criteria below.
crit_vec
1.d-6 # default 1.d-5
crit_e
1.d-8 # default 1.d-7
$END
$resp
geom
norder
1 # first-order nuclear derivative
method
2 # TDDFT response properties
nfiles
1 # must be the same number as the number after the istore keyword in $TDDFT
iroot
1 # calculate the gradient of the first root. Can be omitted here since only
# one root is calculated in the $TDDFT block
$end
注意上述算例中, $resp 模块的关键词 iroot 的意义和前述 $tddft 模块的关键词 iroot 的意义不同。前者指的是计算第几个激发态的梯度,后者则指的是每个不可约表示一共计算多少个激发态。
结构优化收敛后,在主输出文件中输出收敛的结构:
Good Job, Geometry Optimization converged in 5 iterations!
Molecular Cartesian Coordinates (X,Y,Z) in Angstrom :
C -1.92180514 0.07448476 0.00000000
H -2.21141426 -0.98128927 0.00000000
H -2.70870517 0.83126705 0.00000000
C -0.54269837 0.45145649 0.00000000
H -0.31040658 1.52367715 0.00000000
C 0.54269837 -0.45145649 0.00000000
H 0.31040658 -1.52367715 0.00000000
C 1.92180514 -0.07448476 0.00000000
H 2.21141426 0.98128927 0.00000000
H 2.70870517 -0.83126705 0.00000000
Force-RMS Force-Max Step-RMS Step-Max
Conv. tolerance : 0.2000E-03 0.3000E-03 0.8000E-03 0.1200E-02
Current values : 0.5550E-04 0.1545E-03 0.3473E-03 0.1127E-02
Geom. converge : Yes Yes Yes Yes
此外可以从 .out.tmp 文件的最后一个TDDFT模块的输出里读取激发态平衡结构下的激发能,以及激发态的总能量、主要成分:
No. 1 w= 5.1695 eV -155.6874121542 a.u. f= 0.6576 D<Pab>= 0.0000 Ova= 0.8744
CV(0): Ag( 6 )-> Bu( 10 ) c_i: 0.1224 Per: 1.5% IPA: 17.551 eV Oai: 0.6168
CV(0): Bg( 1 )-> Au( 2 ) c_i: -0.9479 Per: 89.9% IPA: 4.574 eV Oai: 0.9035
...
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 Bu 1 Bu 5.1695 eV 239.84 nm 0.6576 0.0000 89.9% CV(0): Bg( 1 )-> Au( 2 ) 4.574 0.874 0.0000
其中,激发态平衡结构下的激发能对应的波长(240 nm)即为丁二烯的荧光发射波长。
备注
某些体系的激发态结构优化会振荡不收敛,这一般是因为优化到了锥形交叉点附近;如果优化到了激发态和基态的锥形交叉点附近,且用的是Full TDDFT而非TDA,则结构优化甚至可能会因激发能变为虚数或复数而报错退出。这两种情况是正常现象,其成因及解决方案详见 几何优化不收敛的解决方法 。
基于sf-X2C/TDDFT-SOC的自旋轨道耦合计算
相对论效应包括标量相对论和自旋轨道耦合(spin-orbit coupling, SOC)。相对论计算需要使用 针对相对论效应优化的基组, 并选择合适的哈密顿 。BDF支持全电子的sf-X2C/TDDFT-SOC计算,这里sf-X2C指用无自旋的精确二分量(eXact Two-Component, X2C)哈密顿考虑标量相对论效应,TDDFT-SOC指基于TDDFT计算自旋轨道耦合。注意虽然TDDFT是激发态方法,但TDDFT-SOC不仅可以用来计算SOC对激发态能量、性质的贡献,也可以用来计算SOC对基态能量、性质的贡献。
以基态为单重态的分子为例,完成sf-X2C/TDDFT-SOC计算需要按顺序调用三次TDDFT计算模块。其中,第一次执行利用R-TDDFT,计算单重态, 第二次利用SF-TDDFT计算三重态,最后一次读入前两个TDDFT计算的波函数,用态相互作用(State interaction, SI)方法 计算这些态的自旋轨道耦合。这从下面 \(\ce{CH2S}\) 分子的sf-X2C/TDDFT-SOC计算的高级输入可以清楚地看出。
$COMPASS
Title
ch2s
Basis # Notice: we use relativistic basis set contracted by DKH2
cc-pVDZ-DK
Geometry
C 0.000000 0.000000 -1.039839
S 0.000000 0.000000 0.593284
H 0.000000 0.932612 -1.626759
H 0.000000 -0.932612 -1.626759
End geometry
$END
$xuanyuan
heff # ask for sf-X2C Hamiltonian
3
hsoc # set SOC integral as 1e+mf-2e
2
$end
$scf
RKS
dft
PBE0
$end
#1st: R-TDDFT, calculate singlets
$tddft
isf
0
idiag
1
iroot
10
itda
0
istore # save TDDFT wave function in the 1st scratch file
1
$end
#2nd: spin-flip tddft, use close-shell determinant as reference to calculate triplets
$tddft
isf # notice here: ask for spin-flip up calculation
1
itda
0
idiag
1
iroot
10
istore # save TDDFT wave function in the 2nd scratch file, must be specified
2
$end
#3rd: tddft-soc calculation
$tddft
isoc
2
nprt # print level
10
nfiles
2
ifgs # whether to include the ground state in the SOC treatment. 0=no, 1=yes
1
imatsoc
8
0 0 0 2 1 1
0 0 0 2 2 1
0 0 0 2 3 1
0 0 0 2 4 1
1 1 1 2 1 1
1 1 1 2 2 1
1 1 1 2 3 1
1 1 1 2 4 1
imatrso
6
1 1
1 2
1 3
1 4
1 5
1 6
idiag # full diagonalization of SO Hamiltonian
2
$end
警告
计算必须按照isf=0,isf=1的顺序进行。当SOC处理不考虑基态(即
ifgs=0)时,计算的激发态数iroot越多,结果越准;当考虑基态(即ifgs=1)时,iroot太多反倒会令精度降低,具体表现为低估基态能量,此时iroot的选取没有固定规则,对于一般体系以几十为宜。
关键词 imatsoc 控制要打印哪些SOC矩阵元<A|hso|B>,
8表示要打印8组旋量态之间的SOC,下面顺序输入了8行整数数组;每一行的输入格式为
fileA symA stateA fileB symB stateB,代表矩阵元 <fileA,symA,stateA|hsoc|fileB,symB,stateB>,其中
fileA symA stateA代表文件fileA中的第symA个不可约表示的第stateA个根;例如1 1 1代表第1个TDDFT计算的第1个不可约表示的第1个根;
0 0 0表示基态
备注
程序每次最多只能打印4000个SOC矩阵元。
耦合矩阵元的打印输出如下,
[tddft_soc_matsoc]
Print selected matrix elements of [Hsoc]
SocPairNo. = 1 SOCmat = < 0 0 0 |Hso| 2 1 1 > Dim = 1 3
mi/mj ReHso(au) cm^-1 ImHso(au) cm^-1
0.0 -1.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000
0.0 0.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000
0.0 1.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000
SocPairNo. = 2 SOCmat = < 0 0 0 |Hso| 2 2 1 > Dim = 1 3
mi/mj ReHso(au) cm^-1 ImHso(au) cm^-1
0.0 -1.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000
0.0 0.0 0.0000000000 0.0000000000 0.0007155424 157.0434003237
0.0 1.0 0.0000000000 0.0000000000 -0.0000000000 -0.0000000000
SocPairNo. = 3 SOCmat = < 0 0 0 |Hso| 2 3 1 > Dim = 1 3
mi/mj ReHso(au) cm^-1 ImHso(au) cm^-1
0.0 -1.0 -0.0003065905 -67.2888361761 0.0000000000 0.0000000000
0.0 0.0 0.0000000000 0.0000000000 -0.0000000000 -0.0000000000
0.0 1.0 -0.0003065905 -67.2888361761 -0.0000000000 -0.0000000000
这里, < 0 0 0 |Hso| 2 2 1 > 表示矩阵元 <S0|Hso|T1> , 分别给出其实部ReHso和虚部ImHso。
由于S0只有一个分量,mi为0。T1(spin S=1)有3个分量(Ms=-1,0,1),用mj对这3个分量编号。
其中 Ms=0 的分量与基态的耦合矩阵元的虚部为 0.0007155424 au 。
警告
对比不同程序结果时需要注意:这里给出的是所谓spherical tensor,而不是cartesian tensor,即T1是T_{-1},T_{0},T_{1},不是Tx,Ty,Tz,两者之间存在酉变换。
SOC计算结果为,
Totol No. of States: 161 Print: 10
No. 1 w= -0.0006 eV
Spin: |Gs,1> 1-th Spatial: A1; OmegaSF= 0.0000eV Cr= 0.0000 Ci= 0.9999 Per:100.0%
SumPer: 100.0%
No. 2 w= 1.5481 eV
Spin: |S+,1> 1-th Spatial: A2; OmegaSF= 1.5485eV Cr= 0.9998 Ci= -0.0000 Per:100.0%
SumPer: 100.0%
No. 3 w= 1.5482 eV
Spin: |S+,3> 1-th Spatial: A2; OmegaSF= 1.5485eV Cr= 0.9998 Ci= 0.0000 Per:100.0%
SumPer: 100.0%
No. 4 w= 1.5486 eV
Spin: |S+,2> 1-th Spatial: A2; OmegaSF= 1.5485eV Cr= 0.9999 Ci= 0.0000 Per:100.0%
SumPer: 100.0%
No. 5 w= 2.2106 eV
Spin: |So,1> 1-th Spatial: A2; OmegaSF= 2.2117eV Cr= -0.9985 Ci= 0.0000 Per: 99.7%
SumPer: 99.7%
No. 6 w= 2.5233 eV
Spin: |S+,1> 1-th Spatial: A1; OmegaSF= 2.5232eV Cr= 0.9998 Ci= 0.0000 Per:100.0%
SumPer: 100.0%
No. 7 w= 2.5234 eV
Spin: |S+,3> 1-th Spatial: A1; OmegaSF= 2.5232eV Cr= 0.9998 Ci= -0.0000 Per:100.0%
SumPer: 100.0%
No. 8 w= 2.5240 eV
Spin: |S+,2> 1-th Spatial: A1; OmegaSF= 2.5232eV Cr= 0.0000 Ci= -0.9985 Per: 99.7%
SumPer: 99.7%
No. 9 w= 5.5113 eV
Spin: |S+,1> 1-th Spatial: B2; OmegaSF= 5.5115eV Cr= -0.7070 Ci= -0.0000 Per: 50.0%
Spin: |S+,3> 1-th Spatial: B2; OmegaSF= 5.5115eV Cr= 0.7070 Ci= 0.0000 Per: 50.0%
SumPer: 100.0%
No. 10 w= 5.5116 eV
Spin: |S+,1> 1-th Spatial: B2; OmegaSF= 5.5115eV Cr= -0.5011 Ci= -0.0063 Per: 25.1%
Spin: |S+,2> 1-th Spatial: B2; OmegaSF= 5.5115eV Cr= 0.7055 Ci= 0.0000 Per: 49.8%
Spin: |S+,3> 1-th Spatial: B2; OmegaSF= 5.5115eV Cr= -0.5011 Ci= -0.0063 Per: 25.1%
SumPer: 100.0%
*** List of SOC-SI results ***
No. ExEnergies Dominant Excitations Esf dE Eex(eV) (cm^-1)
1 -0.0006 eV 100.0% Spin: |Gs,1> 0-th A1 0.0000 -0.0006 0.0000 0.00
2 1.5481 eV 100.0% Spin: |S+,1> 1-th A2 1.5485 -0.0004 1.5487 12491.27
3 1.5482 eV 100.0% Spin: |S+,3> 1-th A2 1.5485 -0.0004 1.5487 12491.38
4 1.5486 eV 100.0% Spin: |S+,2> 1-th A2 1.5485 0.0001 1.5492 12494.98
5 2.2106 eV 99.7% Spin: |So,1> 1-th A2 2.2117 -0.0011 2.2112 17834.44
6 2.5233 eV 100.0% Spin: |S+,1> 1-th A1 2.5232 0.0002 2.5239 20356.82
7 2.5234 eV 100.0% Spin: |S+,3> 1-th A1 2.5232 0.0002 2.5239 20356.99
8 2.5240 eV 99.7% Spin: |S+,2> 1-th A1 2.5232 0.0008 2.5246 20362.08
9 5.5113 eV 50.0% Spin: |S+,1> 1-th B2 5.5115 -0.0002 5.5119 44456.48
10 5.5116 eV 49.8% Spin: |S+,2> 1-th B2 5.5115 0.0001 5.5122 44458.63
这里的输出有两部分,第一部分给出了每个 SOC-SI 态相对于S0态的能量及组成成分,例如
No. 10 w= 5.5116 eV表示第10个SOC-SI态的能量为5.5116 eV,注意这里是相对于S0态的能量;
下面三行是这个态的组成成分,
Spin: |S+,1> 1-th Spatial: B2;代表这是对称性为B2的第一个三重态(相对于S态自旋+1,因而是S+);
OmegaSF= 5.5115eV是相对于第一个旋量态的能量;
Cr= -0.5011 Ci= -0.0063是该成分在旋量态中组成波函数的实部与虚部,所占百分比为25.1%。
第二部分总结了SOC-SI态的计算结果,
ExEnergies列出考虑SOC后的激发能。Esf为原始不考虑SOC时的激发能;激发态表示用
Spin: |S,M> n-th sym来表示,自旋|Gs,1>,空间对称性为sym的第n个态。例如,|Gs,1>代表基态,|So,1>表示总自旋和基态相同的激发态,|S+,2>表示总自旋加1的激发态。M为自旋投影的第几个分量(in total 2S+1)。
关键词 imatrso 指定要计算并打印哪几组旋量态之间的跃迁偶极矩。这里指定打印 6 组跃迁偶极矩,
1 1表示基态固有偶极矩;
1 2表示第一个与第二个旋量态间的跃迁偶极矩。
备注
程序每次最多只能打印4000组跃迁偶极矩。
跃迁偶极矩的输出如下:
[tddft_soc_matrso]: Print selected matrix elements of [dpl]
No. ( I , J ) |rij|^2 E_J-E_I fosc rate(s^-1)
-------------------------------------------------------------------------------
1 1 1 0.472E+00 0.000000000 0.000000000 0.000E+00
Details of transition dipole moment with SOC (in a.u.):
<I|X|J> <I|Y|J> <I|Z|J> (also in debye)
Real= -0.113E-15 -0.828E-18 0.687E+00 -0.0000 -0.0000 1.7471
Imag= -0.203E-35 0.948E-35 0.737E-35 -0.0000 0.0000 0.0000
Norm= 0.113E-15 0.828E-18 0.687E+00
No. ( I , J ) |rij|^2 E_J-E_I fosc rate(s^-1)
-------------------------------------------------------------------------------
2 1 2 0.249E-05 1.548720567 0.000000095 0.985E+01
Details of transition dipole moment with SOC (in a.u.):
<I|X|J> <I|Y|J> <I|Z|J> (also in debye)
Real= -0.589E-03 0.207E-07 -0.177E-15 -0.0015 0.0000 -0.0000
Imag= -0.835E-08 0.147E-02 -0.198E-16 -0.0000 0.0037 -0.0000
Norm= 0.589E-03 0.147E-02 0.178E-15
提示
imatsoc设置为-1可指定打印所有的耦合矩阵元;默认不计算打印跃迁偶极矩,设置
imatrso为-1可以打印所有旋量态之间的跃迁偶极矩,设置imatrso为-2可以打印所有基态旋量态和所有激发态旋量态之间的跃迁偶极矩。SOC计算的参考态必须要么是RHF/RKS,要么是ROHF/ROKS,不支持UHF/UKS。
当SOC计算的参考态为ROHF/ROKS时,isf=0的TDDFT计算必须使用X-TDA(即itest=1, icorrect=1, isf=0, itda=1;不支持full X-TDDFT),isf=1的TDDFT计算必须使用SF-TDA(即isf=1, itda=1;不支持full SF-TDDFT)。
采用ECP基组的TDDFT-SOC自旋轨道耦合计算
除了sf-X2C全电子标量相对论哈密顿以外,也可以用赝势做TDDFT-SOC自旋轨道耦合计算,其中旋轨耦合赝势(SOECP)是首选,
为此需要选择合适的 旋轨耦合赝势基组 ,并在 xuanyuan 模块中设置 hsoc 为10(也可以写其它值,
但是都会当作10处理)。
其它输入与sf-X2C/TDDFT-SOC输入类似(例如在 scf 中指定轨道占据时要扣除芯层电子)或相同。
在下面的例子中,在 \(C_{2v}\) 点群对称性下计算了 InBr 分子的闭壳层基态 \(X^1\Sigma^+\) (A1)和最低三个激发态 \(^3\Pi\) (B1+B2)、 \(^1\Pi\) (B1+B2)、 \(^3\Sigma^+\) (A1),其中前两个Λ-S态是做了大量实验研究的束缚态, 后两个Λ-S态是排斥态,实验上不太关心。 输入中,首先在TDDFT级别下(这里采用Tamm-Dancoff近似)计算了Λ-S态的能量并存储波函,之后计算自旋轨道耦合后的Ω态能量。
$COMPASS
Title
soecp test: InBr
Basis-block
cc-pVTZ-PP
end basis
Geometry
In 0.0 0.0 0.0
Br 0.0 0.0 2.45
END geometry
group
C(2v) # Abelian symmetry must be used for SOC
$END
$XUANYUAN
hsoc
10
$END
$scf
rks
dft
pbe0
$end
$TDDFT
ISF
0
ITDA
1
istore
1
# 1Pi state: A1, A2, B1, B2
nroot
0 0 1 1
$END
$TDDFT
ISF
1
ITDA
1
istore
2
# 3Sigma+ and 3Pi states: A1, A2, B1, B2
nroot
1 0 1 1
$END
$TDDFT
isoc
2
nfiles
2
ifgs
1
idiag
2
$END
SOECP/TDDFT-SOC的计算输出与sf-X2C/TDDFT-SOC类似。结果总结如下,并与二分量EOM-CCSD的结果进行对比。
Λ-S态 |
TDDFT |
Ω态 |
TDDFT-SOC |
分裂 |
二分量EOM-CCSD |
分裂 |
|---|---|---|---|---|---|---|
\(X^1\Sigma^+\) |
0 |
0+ |
0 |
0 |
||
\(^3\Pi\) |
25731 |
0- |
24884 |
24516 |
||
0+ |
24959 |
75 |
24588 |
72 |
||
1 |
25718 |
759 |
25363 |
775 |
||
2 |
26666 |
948 |
26347 |
984 |
||
\(^1\Pi\) |
35400 |
1 |
35404 |
36389 |
||
\(^3\Sigma^+\) |
38251 |
0- |
38325 |
|||
1 |
38423 |
98 |
除了SOECP基组以外,也可以用标量ECP基组结合 有效核电荷近似(Zeff) 完成以上计算。 作为测试,首先删除Br基组中的SO赝势部分,重做上面的计算,但是会发现结果较差: \(^3\Pi_2\) 与 \(^3\Pi_1\) 的分裂只有850 cm \(^{-1}\) ,而 \(^3\Sigma^+\) 态的分裂几乎为零。 这是因为Br具有10个芯电子的ECP基组没有专门优化的有效核电荷,程序只能采用实际的核电荷数35:
SO-1e[BP]
Zeff for Wso
----------------------------------
IAtm ZA NCore Zeff
----------------------------------
1 49 28 SOECP
2 35 10 N.A.
----------------------------------
对于上例中的Br,不妨改用具有28个芯电子的标量ECP基组cc-pVTZ-ccECP,基组的输入部分修改如下:
Basis-block
cc-pvtz-pp
Br=cc-pvtz-ccecp
end basis
在 xuanyuan 之后的模块中未指定轨道占据,因此无需修改输入。在TDDFT-SOC计算输出的一开始可以看到
SO-1e[BP]
Zeff for Wso
----------------------------------
IAtm ZA NCore Zeff
----------------------------------
1 49 28 SOECP
2 35 28 1435.000
----------------------------------
这表明在Br的单电子自旋轨道积分中,用优化好的1435.000替换默认的核电荷数35(一般来说,ECP芯电子数NCore越大,有效核电荷Zeff越大), 而对In原子仍旧计算SOECP积分。计算结果如下,可见旋轨分裂得到了明显改善:
Λ-S态 |
TDDFT |
Ω态 |
Br:SOECP |
分裂 |
Br:ECP |
分裂 |
|---|---|---|---|---|---|---|
\(X^1\Sigma^+\) |
0 |
0+ |
0 |
0 |
||
\(^3\Pi\) |
25731 |
0- |
24884 |
25019 |
||
0+ |
24959 |
75 |
25084 |
65 |
||
1 |
25718 |
759 |
25856 |
772 |
||
2 |
26666 |
948 |
26808 |
952 |
||
\(^1\Pi\) |
35400 |
1 |
35404 |
35729 |
||
\(^3\Sigma^+\) |
38251 |
0- |
38325 |
38788 |
||
1 |
38423 |
98 |
38853 |
65 |
最后,TDDFT-SOC计算也可以用SOECP(或标量ECP)基组与全电子非相对论基组进行组合。 BDF程序已经对Xe之前主族元素的全电子非相对论基组优化了Zeff(较重的稀有气体元素除外)。 例如,In继续用cc-pVTZ-PP,而Br用全电子非相对论基组cc-pVTZ,会得到与SOECP/TDDFT-SOC相近的结果。详细结果从略。
注意
用有效核电荷方法进行TDDFT-SOC计算时的注意事项:必须用 优化好的有效核电荷 才能保证精度。为此要检查输出文件打印的Zeff值,尽量不要出现N.A.,这对ECP基组尤其重要。
SOECP或标量ECP与全电子基组组合时,关于全电子基组的注意事项:由于使用全电子基组的原子不考虑标量相对论相应,因此不能是重原子,且必须用非相对论基组。
一阶非绝热耦合矩阵元(fo-NACME)的计算
如前所述,(一阶)非绝热耦合矩阵元在非辐射跃迁过程中有着重要的意义,其主要用途之一为计算内转换速率常数(参见 BDF-MOMAP联用计算内转换速率常数的示例 )。在BDF中,基态和激发态之间的NACME,以及激发态和激发态之间的NACME的输入文件在写法上存在一定差异,以下分别介绍。
备注
基态和激发态之间的NACME、激发态和激发态之间的NACME均支持R-TDDFT和U-TDDFT,但均暂不支持X-TDDFT。
(1)基态和激发态之间的NACME: \(\ce{NO3}\) 自由基的D0/D1 NACME(GB3LYP/cc-pVDZ)
$COMPASS
Title
NO3 radical NAC, 1st excited state
Basis
cc-pvdz
Geometry
N 0.0000000000 0.0000000000 -0.1945736441
O -2.0700698389 0.0000000000 -1.1615808530
O 2.0700698389 -0.0000000000 -1.1615808530
O -0.0000000000 0.0000000000 2.4934136445
End geometry
unit
bohr
$END
$XUANYUAN
$END
$SCF
UKS
dft
GB3LYP
spinmulti
2
$END
$tddft
iroot
1 # One root for each irrep
istore
1 # File number, to be used later in $resp
crit_vec
1.d-6
crit_e
1.d-8
gridtol
1.d-7 # tighten the tolerance value of XC grid generation. This helps to
# reduce numerical error, and is recommended for open-shell molecules
$end
$resp
iprt
1
QUAD # quadratic response
FNAC # first-order NACME
single # calculation of properties from single residues (ground state-excited
# state fo-NACMEs belong to this kind of properties)
norder
1
method
2
nfiles
1 # must be the same as the istore value in the $TDDFT block
states
1 # Number of excited states for which NAC is requested.
# First number 1: read TDDFT results from file No. 1
# Second number 2: the second irrep, in this case A2
# (note: this is the pair symmetry of the particle-hole pair, not
# the excited state symmetry. One must bear this in mind because the
# ground state of radicals frequently does not belong to the totally
# symmetric irrep)
# If no symmetry is used, simply use 1.
# Third number 1: the 1st excited state that belongs to this irrep
1 2 1
$end
注意 $resp 模块中指定的不可约表示为pair irrep(即跃迁涉及的占据轨道和空轨道的不可约表示的直积;对于阿贝尔点群,pair irrep可以由基态不可约表示和激发态不可约表示的直积求得),而不是激发态的irrep。该分子的基态(D0)属于B1不可约表示,第一二重态激发态(D1)属于B2不可约表示,因此D1态的pair irrep为B1和B2的直积,即A2。Pair irrep也可由TDDFT模块的输出读取得到,即以下输出部分的Pair一栏:
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A2 1 B2 0.8005 eV 1548.84 nm 0.0000 0.0186 98.2% CO(bb): B2( 2 )-> B1( 5 ) 3.992 0.622 0.0000
2 B1 1 A1 1.9700 eV 629.35 nm 0.0011 0.0399 92.2% CO(bb): A1( 8 )-> B1( 5 ) 3.958 0.667 1.1695
3 B2 1 A2 2.5146 eV 493.06 nm 0.0000 0.0384 98.4% CO(bb): A2( 1 )-> B1( 5 ) 4.159 0.319 1.7141
4 A1 2 B1 2.6054 eV 475.87 nm 0.0171 0.0154 87.7% CO(bb): B1( 4 )-> B1( 5 ) 3.984 0.746 1.8049
计算完成后,在 $resp 模块的输出部分的结尾,可以看到NACME的计算结果:
Gradient contribution from Final-NAC(R)-Escaled
1 0.0000000000 -0.0000000000 0.0000000000
2 -0.0000000000 -0.1902838724 0.0000000000
3 -0.0000000000 0.1902838724 0.0000000000
4 -0.0000000000 0.0000000000 0.0000000000
可以发现计算结果有N行(其中N为体系的原子数),每行有3个实数,分别代表该原子的NACME的x、y、z分量。注意该结果没有包括电子平移因子(electron translation factor, ETF)的贡献,对于某些分子,不包括ETF的NACME可能会不具有平移不变性,进而导致后续动力学模拟等计算产生误差。此时需要使用考虑了ETF的NACME,在输出文件稍后的位置可以读取得到:
Gradient contribution from Final-NAC(S)-Escaled
1 0.0000000000 -0.0000000000 0.0000000000
2 -0.0000000000 -0.1920053581 0.0000000000
3 -0.0000000000 0.1920053581 0.0000000000
4 -0.0000000000 0.0000000000 -0.0000000000
程序还会输出名为dpq-R、Final-NAC(R)、dpq-S、Final-NAC(S)等的矢量,这些量是中间变量,仅供监测计算过程使用,并非最终的NACME,一般情况下用户可忽略这些输出。
(2)激发态和激发态之间的NACME:苯乙酮的T1/T2 NACME(BH&HLYP/def2-SVP)
$compass
title
PhCOMe
basis
def2-SVP
geometry
C -0.3657620861 4.8928163606 0.0000770328
C -2.4915224786 3.3493223987 -0.0001063823
C -2.2618953860 0.7463412225 -0.0001958732
C 0.1436118499 -0.3999193588 -0.0000964543
C 2.2879147462 1.1871091769 0.0000824391
C 2.0183382809 3.7824607425 0.0001740921
H -0.5627800515 6.9313968857 0.0001389666
H -4.3630645857 4.1868310874 -0.0002094148
H -3.9523568496 -0.4075513123 -0.0003833263
H 4.1604797959 0.3598389310 0.0001836001
H 3.6948496439 4.9629708946 0.0003304312
C 0.3897478526 -3.0915327760 -0.0002927344
O 2.5733215239 -4.1533492423 -0.0002053903
C -1.8017552120 -4.9131221777 0.0003595831
H -2.9771560760 -4.6352720097 1.6803279168
H -2.9780678476 -4.6353463569 -1.6789597597
H -1.1205416224 -6.8569277129 0.0002044899
end geometry
unit
bohr
nosymm
$end
$XUANYUAN
$END
$SCF
rks
dft
bhhlyp
$END
$tddft
isf # request for triplets (spin flip up)
1
ialda # use collinear kernel (NAC only supports collinear kernel)
4
iroot
2 # calculate T1 and T2 states
crit_vec
1.d-6
crit_e
1.d-8
istore
1
iprt
2
$end
$resp
iprt
1
QUAD
FNAC
double # calculation of properties from double residues (excited state-excited
# state fo-NACMEs belong to this kind of properties)
norder
1
method
2
nfiles
1
pairs
1 # Number of pairs of excited states for which NAC is requested.
1 1 1 1 1 2
noresp # do not include the quadratic response contributions (recommended)
$end
计算得到T1态和T2态的NACME:
Gradient contribution from Final-NAC(R)-Escaled
1 0.0005655253 0.0005095355 -0.2407937116
2 -0.0006501682 -0.0005568029 0.5339003311
3 0.0009640605 0.0003767996 -2.6530192038
4 -0.0013429266 -0.0034063171 1.6760344312
5 0.0010446538 0.0006384285 -0.8024123329
6 -0.0001081722 -0.0006245719 -0.0487310115
7 -0.0000001499 0.0000176176 -0.0730900968
8 -0.0000214634 0.0000165092 0.3841606239
9 0.0000026057 -0.0000025322 -0.2553378323
10 -0.0002028358 -0.0000591642 0.5800987974
11 -0.0000166820 0.0000105734 0.2713836450
12 -0.0023404123 0.0052038311 3.5121827769
13 0.0021749503 -0.0012164868 -2.7480141157
14 0.0000433873 -0.0011202812 0.2896243729
15 0.1407516324 0.1432264573 -0.1655701318
16 -0.1407399684 -0.1429881941 -0.1657943551
17 -0.0000034197 0.0004577563 -0.0833951446
激发态的定域化
$COMPASS
Basis
cc-pvdz
Geometry
C 0.000000 0.000000 0.000000
C 1.332000 0.000000 0.000000
H -0.574301 -0.928785 0.000000
H -0.574301 0.928785 0.000000
H 1.906301 0.928785 0.000000
H 1.906301 -0.928785 0.000000
C -0.000000 0.000000 3.5000
C 1.332000 -0.000000 3.5000
H -0.574301 0.928785 3.50000
H -0.574301 -0.928785 3.50000
H 1.906301 -0.928785 3.50000
H 1.906301 0.928785 3.50000
End geometry
Group
C(1)
Nfragment # must input: number of fragment, should be 1
1
$END
$xuanyuan
$end
$scf
rks
dft
B3lyp
$end
$TDDFT
ITDA
1
IDIAG
1
istore
1
iroot
4
crit_e # set a small threshhold for TDDFT energy convergence
1.d-8
$END
# calculate local excited states (LOCALES)
$elecoup
locales
1
$END
&database
fragment 1 12 # first fragment with 12 atoms, next line gives the atom list
1 2 3 4 5 6 7 8 9 10 11 12
&end
TDA计算了4个激发态,输出如下,
No. Pair ExSym ExEnergies Wavelengths f D<S^2> Dominant Excitations IPA Ova En-E1
1 A 2 A 7.4870 eV 165.60 nm 0.0000 0.0000 82.6% CV(0): A( 16 )-> A( 17 ) 13.476 0.820 0.0000
2 A 3 A 8.6807 eV 142.83 nm 0.0673 0.0000 79.6% CV(0): A( 16 )-> A( 18 ) 14.553 0.375 1.1937
3 A 4 A 9.0292 eV 137.31 nm 0.0000 0.0000 62.4% CV(0): A( 16 )-> A( 20 ) 15.353 0.398 1.5422
4 A 5 A 9.0663 eV 136.75 nm 0.0000 0.0000 50.4% CV(0): A( 15 )-> A( 18 ) 15.688 0.390 1.5793
定域化的过程及定域的激发态为,
No. 8 iteration
Pair States : 1 2
aij,bij,abij -.25659893E-01 -.48045653E-11 0.25659893E-01
cos4a,sin4a 0.10000000E+01 -.18724027E-09
cosa,sina 0.10000000E+01 0.00000000E+00
Pair States : 1 3
aij,bij,abij -.40325646E-02 0.35638586E-11 0.40325646E-02
cos4a,sin4a 0.10000000E+01 0.88376974E-09
cosa,sina 0.10000000E+01 0.00000000E+00
Pair States : 1 4
aij,bij,abij -.25679319E-01 -.28753641E-08 0.25679319E-01
cos4a,sin4a 0.10000000E+01 -.11197197E-06
cosa,sina 0.10000000E+01 0.27877520E-07
Pair States : 2 3
aij,bij,abij -.39851115E-02 -.27118892E-05 0.39851124E-02
cos4a,sin4a 0.99999977E+00 -.68050506E-03
cosa,sina 0.99999999E+00 0.17012628E-03
Pair States : 2 4
aij,bij,abij -.42686102E-02 -.95914926E-06 0.42686103E-02
cos4a,sin4a 0.99999997E+00 -.22469825E-03
cosa,sina 0.10000000E+01 0.56174562E-04
Pair States : 3 4
aij,bij,abij -.67873307E-01 -.47952471E-02 0.68042488E-01
cos4a,sin4a 0.99751360E+00 -.70474305E-01
cosa,sina 0.99984454E+00 0.17632279E-01
Sum= 0.13608498 Max Delta= 0.00531009
No. 9 iteration
Pair States : 1 2
aij,bij,abij -.40325638E-02 0.35621782E-11 0.40325638E-02
cos4a,sin4a 0.10000000E+01 0.88335323E-09
cosa,sina 0.10000000E+01 0.00000000E+00
Pair States : 1 3
aij,bij,abij -.25690755E-01 -.11200070E-08 0.25690755E-01
cos4a,sin4a 0.10000000E+01 -.43595721E-07
cosa,sina 0.10000000E+01 0.10536712E-07
Pair States : 1 4
aij,bij,abij -.25690755E-01 -.10900573E-11 0.25690755E-01
cos4a,sin4a 0.10000000E+01 -.42429944E-10
cosa,sina 0.10000000E+01 0.00000000E+00
Pair States : 2 3
aij,bij,abij -.41480079E-02 -.83549288E-06 0.41480080E-02
cos4a,sin4a 0.99999998E+00 -.20142027E-03
cosa,sina 0.10000000E+01 0.50355067E-04
Pair States : 2 4
aij,bij,abij -.41480100E-02 0.17462423E-06 0.41480100E-02
cos4a,sin4a 0.10000000E+01 0.42098314E-04
cosa,sina 0.10000000E+01 0.10524580E-04
Pair States : 3 4
aij,bij,abij -.68042492E-01 0.19389042E-08 0.68042492E-01
cos4a,sin4a 0.10000000E+01 0.28495490E-07
cosa,sina 0.10000000E+01 0.74505806E-08
Sum= 0.13608498 Max Delta= 0.00000000
***************** Diabatic Hamiltonian matrix ****************
State1 State2 State3 State4
State1 7.486977 0.000000 0.000000 0.000000
State2 0.000000 9.029214 -0.000020 0.000021
State3 0.000000 -0.000020 8.873501 0.192803
State4 0.000000 0.000021 0.192803 8.873501**************************************************************
其中,对角元为定域激发态的能量,非对角元为两个定域态之间的耦合,这里的能量单位是 eV 。
核磁共振屏蔽常数
BDF支持限制性Hartree-Fock(RHF)和限制性Kohn-Sham(RKS)方法的核磁共振屏蔽常数(NMR)计算, 其中外矢势规范原点的问题可以使用Common gauge方法和GIAO(gauge-including atomic orbitals)处理。
警告
由于NMR计算需要libcint库,需要在计算脚本中增加一行: export USE_LIBCINT=yes
NMR算例
以下为甲烷分子核磁共振屏蔽常数计算的输入文件:
$COMPASS # 分子坐标输入及对称性判断等
Title
CH4 Molecule NR-DFT-NMR # job title
Basis
CC-PVQZ # basis set
Geometry
C 0.000 00000 0.000 # molecule geometry
H 1.196 1.196 1.196
H -1.196 -1.196 1.196
H -1.196 1.196 -1.196
H 1.196 -1.196 -1.196
END geometry
nosymm # NMR模块暂不支持对称性
UNIT
BOHR # input molecule geometry in bohr
$END
$xuanyuan # 单双电子积分相关设定和计算
$end
$SCF # 自洽场计算模块
RKS # Restrict Kohn-Sham
DFT
b3lyp
$END
$NMR # 核磁共振屏蔽常数计算模块
icg
1 # 可输入0或1,0为不进行COMMON GAUGE计算,1为进行COMMON GAUGE计算,默认为0
igiao
1 # 可输入0或1,0为不进行GIAO计算,1为进行GIAO计算,默认为0
$END
完成计算将顺序调用 compass , xuanyuan , scf 及 nmr 四个模块。其中 scf 模块执行 RKS 计算。
基于RKS的计算结果,进行后续的 NMR 计算,其中 NMR 计算将顺序进行COMMON GAUGE计算和GIAO计算,计算将给出所有原子的
各向同性以及各向异性核磁共振屏蔽常数。
COMMON GAUGE
可以通过关键词icg控制进行COMMON GAUGE的NMR计算:
$NMR
icg
1
$END
可以输入0或者1,默认值为0,即不进行COMMON GAUGE计算,输入为1时,则为进行COMMON GAUGE计算。
在COMMON GAUGE计算中,规范原点默认位于坐标原点,即(0,0,0)处,可以通过关键词igatom将规范原点指定在某个原子上, 也可以通过cgcoord将规范原点设置为空间某个指定的位置,具体输入方式如下:
$NMR
icg
1
igatom
3 # 将规范原点指定在3号原子上,输入为整型数,范围为0到分子原子数,
# 如输入值0,则将规范原点指定在坐标原点上
cgcoord
1.0 0.0 0.0 # 输入为3个实型数,将规范原点至于空间坐标为(1.0,0.0,0.0)的点上
cgunit
angstrom # cgcoord坐标的单位,默认值为原子单位,当输入为angstrom,输入的规范原点坐标
# 单位为埃;其他输入(如bohr,AU),坐标单位为原子单位,输入不区分大小写
$END
当输入中同时存在igatom和cgcoord时,以后输入的为准。例如上面的例子,最终规范原点设定在空间坐标为(1.0,0.0,0.0)(单位埃)的位置上。 如两个参数igatom和cgcoord都未输入,计算COMMON GAUGE的NMR值时,规范原点设在坐标原点上,即设在(0.0,0.0,0.0)的位置上。
输出文件中Common gauge计算从 [nmr_nr_cg] 开始,如下:
[nmr_nr_cg]
Doing nonrelativistic-CG-DFT nmr...
[nmr_set_common_gauge]
set the common gauge origin as the coordinate origin(default)
0.000000000000 0.000000000000 0.000000000000
略过中间部分输出,最终结果输出如下:
Isotropic/anisotropic constant by atom type:
atom-C
186.194036 0.000003
atom-H
31.028177 9.317141
31.028176 9.317141
31.028177 9.317141
31.028177 9.317141
分别为C原子和H原子的核磁共振屏蔽常数,单位为ppm,第一列为各向同性屏蔽常数,第二列为各向异性屏蔽常数。
GIAO
可以通过关键词igiao控制进行GIAO的NMR计算:
$NMR
igiao
1
$END
可以输入0或者1,默认值为0,即不进行GIAO计算,输入为1时,进行GIAO计算。
警告
NMR模块中,icg和igiao可以仅输入其中之一为1,即设定进行其中一种计算,也可以两者都输入设为1(即两种计算都进行),但是不能都不输入或者都设为0, 不然NMR模块不会得出任何核磁共振屏蔽常数值。
输出文件中GIAO计算从 [nmr_nr_giao] 开始,如下:
[nmr_nr_giao]
Doing nonrelativistic-GIAO-DFT nmr
[set_para_for_giao_eri]
[nmr_int]
Doing nmr integral of operators resulting from the response of B10...
No. of pGTOs and cGTOs: 196 196
giao integrals...
略过中间部分输出,最终结果输出如下:
Isotropic/anisotropic constant by atom type:
atom-C
186.461988 0.000019
atom-H
31.204947 9.070916
31.204944 9.070916
31.204947 9.070921
31.204946 9.070920
同COMMON GAUGE的情况,上面结果分别为C原子和H原子的GIAO核磁共振屏蔽常数,单位为ppm, 第一列为各向同性屏蔽常数,第二列为各向异性屏蔽常数。
警告
输出中的关键词 Isotropic/anisotropic constant by atom type 对于
GIAO与COMMON GAUGE完全相同,在读取结果时应注意是在 [nmr_nr_cg] 后的,
还是 [nmr_nr_giao] 后的,来区分COMMON GAUGE的结果还是GIAO的结果
相对论效应
相对论效应主要包括标量相对论效应和旋轨耦合作用两部分。 相对论效应在有机发光机理研究十分重要,例如旋轨耦合作用导致电子态发生系间窜跃,以及过渡态、产物的自旋发生改变。 原子最内层的芯电子一方面受相对论效应的影响最强,另一方面对化学变化不敏感,因此有不同的处理方式,主要有全电子相对论和有效芯势(ECP)两类方法。
1. 全电子方法 所有的内层电子均做变分处理。常见的全电子相对论哈密顿量有:零阶正则近似(ZORA),二阶Douglas-Kroll-Hess(DKH2), 刘文剑等人提出的精确二分量(X2C),等。ZORA和DKH2在精度和效率上没有优势,不建议使用。
2. ECP 重原子的芯层电子用事先拟合好的有效势函数替代。当重原子较多的情况下,ECP能够大幅降低变分自由度,提高计算效率。根据价电子波函数在芯层有无节点, ECP又分为赝势(PP)和模型芯势(MCP)两大类,其中MCP为了正确地重现价电子波函数节点,必须结合大量的高斯函数,导致计算效率的提升不明显,因此应用较少。 BDF程序中的ECP均指PP。
BDF基组库提供大量的 全电子相对论基组 和 ECP基组 。
警告
X2C哈密顿与ECP基组不要混用
X2C相对论计算必须采用非收缩基组或专门优化的收缩基组,但前18号元素不强求
标量相对论效应
全电子方法
BDF可以通过无自旋X2C哈密顿(sf-X2C)及其局域近似变体sf-X2C-AXR、sf-X2C-AU,考虑标量相对论效应。例如:
$xuanyuan
heff
23
nuclear
1
$end
在以上输入中, heff 调用标量相对论哈密顿,如sf-X2C(3,4,或21),sf-X2C-AXR(原子X矩阵近似,22),
sf-X2C-AU(原子U变换近似,23),其中21,22,23具有解析导数。
nuclear 选项设为1表示使用有限核模型,一般不是必须的。但是有些相对论收缩基组考虑了原子核尺寸效应(如ANO-R),或者当计算原子核附近的电子性质时,这些情况下要使用有限核模型。
那么,sf-X2C和它的变体之间有什么区别呢? sf-X2C通过严格求解分子的单电子无自旋Dirac方程来获得 X 矩阵,是标准做法;当基函数个数超过1000以后,对角化步骤成为计算瓶颈。 sf-X2C-AXR和sf-X2C-AU巧妙利用了 X 矩阵的原子局域性,只需对原子的各个L壳层分别求解维度很小的Dirac方程,得到一些小 X 矩阵,再拼合出分子的大 X 矩阵,因此大大降低了计算量。 基函数个数超过2000以后, R 矩阵的计算也存在类似的问题,sf-X2C-AU利用了 R 矩阵的原子局域性(不过对于超重元素,这一近似略显粗糙), 效率高于严格计算分子 R 矩阵的sf-X2C-AXR。 [27] 因此,对于不涉及5d以上重元素—重元素成键的分子体系,sf-X2C-AU具有最高的效率且不损失精度,是推荐方法。否则用sf-X2C(小分子)或sf-X2C-AXR(大小分子均可)。
警告
heff = 21,22,23时,程序优先从 BDF_TMPDIR 目录下的临时文件中读取解析导数所需的数据,如果临时文件是其它计算产生的,可能会导致错误结果!
此时必须使用空的BDF_TMPDIR目录进行计算,除非原子排序、坐标、基组在两个计算中完全一致。
ECP
ECP必须与非相对论哈密顿相结合,相对论效应隐含在赝势参数中。
旋轨耦合作用
BDF可以通过态相互作用(SI)方法,在TDDFT单点计算中处理不同自旋多重度电子态之间的自旋轨道耦合。需要在 xuanyuan 模块中通过
hsoc 关键词指定如何计算自旋轨道积分。参见 TDDFT 部分的示例。
关于在化学反应模拟中近似考虑旋轨耦合,参见 自旋混合态 计算。
根据采用的哈密顿的不同,自旋轨道耦合也可分为全电子和ECP两类。
全电子方法
尽管双电子SO积分的贡献小于单电子SO积分,但是对旋轨耦合作用的影响可能达到 20% 至 30%,因此不能忽略。有两类处理方法:
单独计算双电子SO积分,其中可以引入一些近似将低计算量。它可以与sf-X2C标量相对论哈密顿结合,对于轻元素体系也可以与非相对论哈密顿结合。
从单电子SO积分估算双电子SO积分,例如屏蔽原子核 [70, 71] 校正,有效核电荷 [72] 校正。这比前一种方法更快,但是精度较低,并且对芯电子性质会造成无法预料的误差。
BDF仅支持第一类处理方法,建议采用单电子SO积分+单中心近似的分子平均场双电子SO积分(so1e + SOMF-1c),在 xuanyuan 模块中把关键词 hsoc 设为 2。
ECP
包括两种处理方法:
旋轨耦合赝势,适用于SOECP描述的原子。需要在标量ECP中加入额外的SO势函数(SOECP;见基组库中的 旋轨耦合赝势基组 )。
有效核电荷 [72, 73] ,适用于标量ECP描述的原子,以及用非相对论全电子基组描述的原子,但是支持的原子类型有限(见下)。
由于双电子自旋轨道相互作用的影响已经包含在SO势的拟合参数或有效核电荷的经验参数中,只要计算单电子SO积分即可。
根据每个原子的基组是否包含SOECP,BDF可以同时使用以上两种处理方法,只需要在 xuanyuan 模块中设定 hsoc 为10。
需要注意的是,有效核电荷支持的元素和基组类型有限。对于全电子基组,仅支持Xe之前的主族元素,且较重的稀有气体元素Ne、Ar、Kr除外。 对于标量ECP基组,虽然支持的元素更多,但是ECP的芯电子数(NCore)必须与下表一致。如果有效核电荷方法用于不支持的元素或基组,旋轨耦合计算的结果不可靠。
原子 |
ZA |
NCore |
|---|---|---|
Li-F |
3- 9 |
2 |
Na-Cl, Sc-Cu, Zn, Ga |
11-17, 21-29, 30, 31 |
10 |
K -Ca |
19-20 |
18 |
Ge-Br, Y -Ag, Cd, In |
32-35, 39-47, 48, 49 |
28 |
Rb-Sr |
37-38 |
36 |
Sn-I, La |
50-53, 57 |
46 |
Cs-Ba |
55-56 |
54 |
Hf-Au, Hg, Tl |
72-79, 80, 81 |
60 |
Pb-At |
82-85 |
78 |
更多细节,如有效核电荷参数、参考文献等,见源文件soint_util/zefflib.F90。
QM/MM组合方法
QM/MM组合方法一般把系统分为两个区域,QM区和MM区。将体系总能量写为:
其中, S 表示系统, I 表示QM层, O表示MM层,L表示链接原子。 \(E_{MM}(\mathbb{O})\) 采用分子力学力场计算, \(E_{QM/MM}(\mathbb{I,O})\) 包括两项:
\(E_{nuc-MM}+V_{elec-MM}\) 在BDF中通过在QM区加入外部点电荷来实现。
所以整个体系的总能量包括两个部分,\(E_{MM}\) 采用分子力学方法计算,\(E_{QM}\) 和 \(E_{QM/MM}\) 采用量子化学方法计算。同时,QM区和MM区的相互作用还包括VDW相互作用等,这里不再赘述。对于QM区和MM区的断键,一般采用链接原子模型来描述。
BDF程序主要完成量子化学计算部分,其余部分由课题组修改的pdynamo2.0程序包完成。具体见相关算例。
备注
pdynamo 程序的安装见程序包中相关说明。有关程序包的详细功能见程序包中的帮助文件。 本手册只提供使用BDF进行QM/MM计算的相关说明和算例。
QM/MM计算环境安装和配置参考:QM/MM计算环境配置
输入文件准备
一般来说,QM/MM计算之前,需要对目标体系进行分子动力学模拟,得到适合的初始构象。不同的分子动力学软件,输出文件不尽相同,
pDynamo-2目前支持 Amber、CHARMM、Gromacs 等力场,同时支持 PDB、MOL2、xyz 等格式读入分子坐标。
备注
当采用PDB、MOL2或xyz文件作为输入时,pDynamo 程序仅支持OPLS力场,对于小分子和非标准氨基酸力场参数不全,不推荐使用。建议优先采用Amber程序, 通过拓扑文件输入力场参数。如果只做QM计算,各种输入方法都可以。
以Amber为例,从动力学模拟轨迹提取感兴趣的结构存储于 crd 文件中,与对应的拓扑文件 .prmtop 一起可以作为QM/MM计算的
起始点。Python 脚本如下:
from pBabel import AmberCrdFile_ToCoordinates3, AmberTopologyFile_ToSystem
# 读取输入信息
molecule = AmberTopologyFile_ToSystem(Topfile)
molecule.coordinates3 = AmberCrdFile_ToCoordinates3(CRDfile)
此时,分子信息存储于 molecule 结构中。具体QM/MM计算中,需要对体系进行能量计算、几何构型优化等操作。同时,可以在MM区定义活性区域,加速计算。
总能量计算
以10埃的水盒子为例,分子动力学模拟后提取文件为 wat.prmtop, wat.crd ,可对体系进行全量子化学计算,代码如下:
import glob, math, os
from pBabel import AmberCrdFile_ToCoordinates3, AmberTopologyFile_ToSystem
from pCore import logFile
from pMolecule mport QCModelBDF, System
# 读取水盒子坐标和拓扑信息
molecule = AmberTopologyFile_ToSystem ("wat.prmtop")
molecule.coordinates3 = AmberCrdFile_ToCoordinates3("wat.crd")
# 定义能量计算模式,此处为全体系密度泛函计算,GB3LYP:6-31g
model = QCModelBDF("GB3LYP:6-31g")
molecule.DefineQCModel(model)
molecule.Summary() #输出体系计算设置信息
# 计算总能量
energy = molecule.Energy()
在 QCModelBDF 类中可以定义方法和基组 GB3LYP:6-31g, 方法和基组间采用 : 分割。上例中也可以选择感兴趣的分子(比如,第五个水分子)
进行QM/MM计算,第五个水分子用QM方法来算,其余用MM(本例中为amber力场)来计算。由于在MD计算时采用周期性边界条件,而QM/MM方法不支持使用周期性边界
条件,所以在脚本中加入选项,关闭周期性边界条件。
molecule.DefineSymmetry( crystalClass = None )
在pDynamo 定义了类 Selection 可以用于选择特定的QM原子,具体见使用说明。选择QM原子的脚本如下:
qm_area = Selection.FromIterable(range(12, 15))
#12、13、14为原子列表索引值(该值 = 原子序号 - 1),等于选择 15号水分子
molecule.DefineQCModel(qcModel, qcSelection = qm_area)
总体,QM/MM组合能量计算的脚本如下:
import glob, math, os
from pBabel import AmberCrdFile_ToCoordinates3, AmberTopologyFile_ToSystem
from pCore import logFile, Selection
from pMolecule import NBModelORCA, QCModelBDF, System
# . Define the energy models.
nbModel = NBModelORCA()
qcModel = QCModelBDF("GB3LYP:6-31g")
# . Read the data.
molecule = AmberTopologyFile_ToSystem("wat.prmtop")
molecule.coordinates3 = AmberCrdFile_ToCoordinates3("wat.crd")
# .Close symmetry to a system
molecule.DefineSymmetry(crystalClass = None) # QM/MM need Close the symmetry.
# .Selection qm area
qm_area = Selection.FromIterable(range (12, 15)) # Select WAT 5 as the QM area.
# . Define the energy model.
molecule.DefineQCModel (qcModel, qcSelection = qm_area)
molecule.DefineNBModel (nbModel)
molecule.Summary()
# . Calculate
energy = molecule.Energy()
备注
QM/MM计算支持两种输入模式,对于简单的算例,可以在
QCModelBDF类中作为参数输入。相对复杂的算例可以采用
计算模版方式输入。
几何构型优化
QM/MM几何构型优化一般不容易收敛,在实际操作中需要的技巧较多。常见的有,固定MM区,优化QM区;然后固定QM区优化MM区。如此往复循环几次后,再同时优化QM区和MM区。 优化是否收敛,和QM区的选择及QM/MM边界是否有带电较多的原子等关系很大。为了加速优化,可以在计算时固定MM区,仅选择离QM区较近的合适区域,作为活性区域,在优化中 坐标可以变化。以下为几何构型优化的算例:
import glob, math, os.path
from pBabel import AmberCrdFile_ToCoordinates3, \
AmberTopologyFile_ToSystem , \
SystemGeometryTrajectory , \
AmberCrdFile_FromSystem , \
PDBFile_FromSystem , \
XYZFile_FromSystem
from pCore import Clone, logFile, Selection
from pMolecule import NBModelORCA, QCModelBDF, System
from pMoleculeScripts import ConjugateGradientMinimize_SystemGeometry
# 定义 Opt interface
def opt_ConjugateGradientMinimize(molecule, selection):
molecule.DefineFixedAtoms(selection) # Define 固定原子
#定义优化方法
ConjugateGradientMinimize_SystemGeometry(
molecule,
maximumIterations = 4, # 最大优化步数
rmsGradientTolerance = 0.1, #优化收敛控制
trajectories = [(trajectory, 1)]
) # 定义轨迹保存频率
# . Define the energy models.
nbModel = NBModelORCA()
qcModel = QCModelBDF("GB3LYP:6-31g")
# . Read the data.
molecule = AmberTopologyFile_ToSystem ("wat.prmtop")
molecule.coordinates3 = AmberCrdFile_ToCoordinates3("wat.crd")
# . Close symmetry to a system
molecule.DefineSymmetry(crystalClass = None) # QM/MM need Close the symmetry.
#. Define Atoms List
natoms = len(molecule.atoms) # 系统中总原子数
qm_list = range(12, 15) # QM 区原子
activate_list = range(6, 12) + range (24, 27) # MM区活性原子(优化中可以移动)
#定义MM区原子
mm_list = range (natoms)
for i in qm_list:
mm_list.remove(i) # MM 删除QM原子
mm_inactivate_list = mm_list[:]
for i in activate_list :
mm_inactivate_list.remove(i)
# 输入QM原子
qmmmtest_qc = Selection.FromIterable(qm_list) # Select WAT 5 as the QM area.
# 定义各选择区
selection_qm_mm_inactivate = Selection.FromIterable(qm_list + mm_inactivate_list)
selection_mm = Selection.FromIterable(mm_list)
selection_mm_inactivate = Selection.FromIterable(mm_inactivate_list)
# . Define the energy model.
molecule.DefineQCModel(qcModel, qcSelection = qmmmtest_qc)
molecule.DefineNBModel(nbModel)
molecule.Summary()
#计算优化开始时总能量
eStart = molecule.Energy()
#定义输出文件
outlabel = 'opt_watbox_bdf'
if os.path.exists(outlabel):
pass
else:
os.mkdir (outlabel)
outlabel = outlabel + '/' + outlabel
# 定义输出轨迹
trajectory = SystemGeometryTrajectory (outlabel + ".trj" , molecule, mode = "w")
# 开始第一阶段优化
# 定义优化两步
iterations = 2
# 顺次固定QM区和MM区进行优化
for i in range(iterations):
opt_ConjugateGradientMinimize(molecule, selection_qm_mm_inactivate) #固定QM区优化
opt_ConjugateGradientMinimize(molecule, selection_mm) #固定MM区优化
# 开始第二阶段优化
# QM区和MM区同时优化
opt_ConjugateGradientMinimize(molecule, selection_mm_inactivate)
#输出优化后总能量
eStop = molecule.Energy()
#保存优化坐标, 可以为xyz/crd/pdb等。
XYZFile_FromSystem(outlabel + ".xyz", molecule)
AmberCrdFile_FromSystem(outlabel + ".crd" , molecule)
PDBFile_FromSystem(outlabel + ".pdb" , molecule)
QM/MM-TDDFT算例
在几何构型优化结束后,可基于QM/MM计算得到的基态进行TDDFT计算。BDF程序接口设计了 计算模版 功能,可基于用户给定的 .inp 文件,更新系统坐标
进行计算。同时,在几何构型优化和激发态计算过程中,可根据需要选择不同的QM区域。比如,为了考虑溶剂化效应,可以把感兴趣的分子的第一水合层添加到QM区进行
QM/MM-TDDFT计算。以前一节中完成的算例为例,可以继续添加如下代码进行计算。
#接前一节几何构型优化代码。
#开始TDDFT计算。使用模版文件作为输入。
qcModel = QCModelBDF_template(template = 'head_bdf_nosymm.inp')
# 调整QM区原子
tdtest = Selection.FromIterable(qm_list + activate_list) # Redefine the QM region.
molecule.DefineQCModel(qcModel, qcSelection = tdtest)
molecule.DefineNBModel(nbModel)
molecule.Summary()
#采用模版中的方法进行能量计算,(可以是TDDFT)
energy = molecule.Energy()
上面代码中,选用的模版为BDF的输入文件,文件内容如下:
$COMPASS
Title
cla_head_bdf
Basis
6-31g
Geometry
H 100.723 207.273 61.172
MG 92.917 204.348 68.063
C 95.652 206.390 67.185
END geometry
Extcharge
point
nosymm
$END
$XUANYUAN
RSOMEGA
0.33
$END
$SCF
RKS
DFT
cam-B3LYP
$END
$tddft #TDDFT计算控制
iprt
3
iroot
5
$end
结构优化与频率计算
结构优化的目的是找到体系势能面的极小点。能找到哪个极小点取决于输入文件中提供的初始结构,离哪个极小点越近,一般越容易收敛到哪个极小点。
结构优化在数学上等价于寻找多元函数极值问题:
结构优化常用算法如下:
最速下降法(Steepest descent):最速下降法就是沿着负梯度的方向进行线搜索,对于远离极小点的结构,最速下降法优化效率非常高,但临近极小点时收敛慢,容易震荡。
共轭梯度法(Conjugate gradient):共轭梯度法是最速下降法的改良,每步优化方向与前一步的优化方向相组合,能一定程度缓解震荡问题。
牛顿法(Newton method):牛顿法的思路是将函数相对于当前位置进行泰勒级数展开。牛顿法收敛很快,对于二次函数一步就可以走到极小点。但是牛顿法需要求解Hessian矩阵,计算非常昂贵,一般几何优化中使用准牛顿法。
准牛顿法(Quasi-Newton method):准牛顿法通过近似方法构建 Hessian矩阵,当前步的Hessian矩阵基于当前步的受力和上一步的Hessian矩阵来得到。具体做法有多种,最常用的是BFGS法,此外还有DFP、MS、PSB等。由于准牛顿法的 Hessian是近似构建的,所以每一步优化的准确度低于牛顿法,达到收敛所需步数较牛顿法更多。但由于每一步耗时大为降低,所以优化总耗时还是显著减少了。
BDF的结构优化是由BDFOPT模块来实现的,支持基于牛顿法和准牛顿法来进行极小值点结构和过渡态结构的优化,且支持限制性结构优化等。以下对BDFOPT模块的输入文件格式举例进行介绍,并对输出文件进行解读。
基态结构优化:一氯甲烷( \(\ce{CH3Cl}\) )在B3LYP/def2-SV(P)水平下的结构优化
$compass
title
CH3Cl geomopt
basis
def2-SV(P)
geometry
C 2.67184328 0.03549756 -3.40353093
H 2.05038141 -0.21545378 -2.56943947
H 2.80438882 1.09651909 -3.44309081
H 3.62454948 -0.43911916 -3.29403269
Cl 1.90897396 -0.51627638 -4.89053325
end geometry
$end
$bdfopt
solver
1
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
其中RESP模块负责计算DFT梯度。与其他大部分任务不同,在结构优化任务中,程序并不是按顺序、单次、线性地调用各模块,而是会反复多次调用各模块。具体的调用顺序为:
运行COMPASS,读取分子结构等信息;
运行BDFOPT,对结构优化所需的中间量进行初始化;
BDFOPT启动一个独立的BDF进程,用来计算当前结构下的能量和梯度,该进程只执行COMPASS、XUANYUAN、SCF、RESP各模块,而跳过BDFOPT。也即,大部分时候用户会发现有两个BDF进程在彼此独立地运行,其中一个为BDFOPT所属的进程,处于等待状态,而另一个进程则在进行能量和梯度的计算。为避免输出文件过于杂乱,后一个进程的输出会被自动重定向到后缀为
.out.tmp的文件,从而与BDFOPT模块的输出(一般会被用户重定向到.out文件)分开;待后一个进程结束时,BDFOPT汇总当前结构的能量和梯度信息,并据此调整分子结构,以期降低体系能量;
BDFOPT根据当前结构的梯度以及当前几何结构步长(geometry step)的大小,判断结构是否收敛,如收敛,或结构优化达到最大迭代次数,则程序结束;如不收敛,则跳至第3步。
因此, .out 文件只包含COMPASS和BDFOPT模块的输出,可以用来监测结构优化的进程,但不包含SCF迭代、布居分析等信息,后者需要在 .out.tmp 文件中查看。
以上述 \(\ce{CH3Cl}\) 的结构优化任务为例,可以看到 .out 文件里BDFOPT模块的输出:
Geometry Optimization step : 1
Single Point SCF for geometry optimization, also get force.
### [bdf_single_point] ### nstate= 1
Allow rotation to standard orientation.
BDFOPT run - details of gradient calculations will be written
into .out.tmp file.
...
### JOB TYPE = SCF ###
E_tot= -499.84154693
Converge= YES
### JOB TYPE = RESP_GSGRAD ###
Energy= -499.841546925072
1 0.0016714972 0.0041574983 -0.0000013445
2 -0.0002556962 -0.0006880567 0.0000402277
3 -0.0002218807 -0.0006861734 -0.0000225761
4 -0.0003229876 -0.0006350885 -0.0000059774
5 -0.0008670369 -0.0021403962 -0.0000084046
可以看到BDFOPT调用了BDF程序本身,来计算初猜结构下分子的SCF能量和梯度。SCF和梯度计算的详细输出在 .out.tmp 文件中,而 .out 文件仅摘取能量值、梯度值,以及SCF是否收敛等信息。其中,能量的单位为Hartree,梯度的单位为Hartree/Bohr。
solver = 1 表示使用BDF自身的优化器,在冗余内坐标下进行结构的优化。
为了产生下一步的分子结构,必须先产生分子的冗余内坐标。
因此在第一步结构优化时,输出文件还会给出各个冗余内坐标的定义(即参与形成相应的键、键角、二面角的原子编号),
以及它们的值(键长的单位为埃,键角、二面角的单位为度):
|******************************************************************************|
Redundant internal coordinates on Angstrom/Degree
Name Definition Value Constraint
R1 1 2 1.0700 No
R2 1 3 1.0700 No
R3 1 4 1.0700 No
R4 1 5 1.7600 No
A1 2 1 3 109.47 No
A2 2 1 4 109.47 No
A3 2 1 5 109.47 No
A4 3 1 4 109.47 No
A5 3 1 5 109.47 No
A6 4 1 5 109.47 No
D1 4 1 3 2 -120.00 No
D2 5 1 3 2 120.00 No
D3 2 1 4 3 -120.00 No
D4 3 1 4 2 120.00 No
D5 5 1 4 2 -120.00 No
D6 5 1 4 3 120.00 No
D7 2 1 5 3 120.00 No
D8 2 1 5 4 -120.00 No
D9 3 1 5 2 -120.00 No
D10 3 1 5 4 120.00 No
D11 4 1 5 2 120.00 No
D12 4 1 5 3 -120.00 No
|******************************************************************************|
待分子结构更新完成后,程序计算梯度以及几何步长的大小,判断结构优化是否收敛:
Force-RMS Force-Max Step-RMS Step-Max
Conv. tolerance : 0.2000E-03 0.3000E-03 0.8000E-03 0.1200E-02
Current values : 0.8833E-02 0.2235E-01 0.2445E-01 0.5934E-01
Geom. converge : No No No No
仅当均方根力(Force-RMS)、最大力(Force-Max)、均方根步长(Step-RMS)、最大步长(Step-Max)的当前值均小于对应的收敛限的时候(也即 Geom. converge 栏均为Yes),程序才认为结构优化收敛。对于本算例,结构优化在第5步时收敛,此时输出信息不仅包含各收敛判据的值,还会明确告知用户几何优化已收敛,并分别以笛卡尔坐标和内坐标的形式打印收敛的分子结构:
Good Job, Geometry Optimization converged in 5 iterations!
Molecular Cartesian Coordinates (X,Y,Z) in Angstrom :
C -0.93557703 0.15971089 0.58828595
H -1.71170348 -0.52644336 0.21665897
H -1.26240747 1.20299703 0.46170050
H -0.72835075 -0.04452039 1.64971607
Cl 0.56770184 -0.09691413 -0.35697029
Force-RMS Force-Max Step-RMS Step-Max
Conv. tolerance : 0.2000E-03 0.3000E-03 0.8000E-03 0.1200E-02
Current values : 0.1736E-05 0.4355E-05 0.3555E-04 0.6607E-04
Geom. converge : Yes Yes Yes Yes
Print Redundant internal coordinates of the converged geometry
|******************************************************************************|
Redundant internal coordinates on Angstrom/Degree
Name Definition Value Constraint
R1 1 2 1.1006 No
R2 1 3 1.1006 No
R3 1 4 1.1006 No
R4 1 5 1.7942 No
A1 2 1 3 110.04 No
A2 2 1 4 110.04 No
A3 2 1 5 108.89 No
A4 3 1 4 110.04 No
A5 3 1 5 108.89 No
A6 4 1 5 108.89 No
D1 4 1 3 2 -121.43 No
D2 5 1 3 2 119.28 No
D3 2 1 4 3 -121.43 No
D4 3 1 4 2 121.43 No
D5 5 1 4 2 -119.28 No
D6 5 1 4 3 119.29 No
D7 2 1 5 3 120.00 No
D8 2 1 5 4 -120.00 No
D9 3 1 5 2 -120.00 No
D10 3 1 5 4 120.00 No
D11 4 1 5 2 120.00 No
D12 4 1 5 3 -120.00 No
|******************************************************************************|
注意此处的均方根力和均方根步长的收敛限可以分别通过 tolgrad 和 tolstep 关键词来设定,程序自动根据设定值来调整最大力和最大步长的收敛限;当使用DL-FIND库时(见后),还可用 tolene 指定能量收敛限。不过一般不建议用户自行调整收敛限。
与此同时,程序还会产生后缀为 .optgeom 的文件,其内容是优化后的分子结构的笛卡尔坐标(若是一般的单点计算,则为当前结构在标准取向下的笛卡尔坐标),但单位为Bohr而非Angstrom:
GEOM
C -0.7303234729 -2.0107211546 -0.0000057534
H -0.5801408002 -2.7816264533 1.9257943885
H 0.4173171420 -3.1440530286 -1.3130342173
H -2.7178161476 -2.0052051760 -0.6126883555
Cl 0.4272106261 1.1761889168 -0.0000021938
.optgeom 文件可以用 $BDFHOME/sbin/ 下的工具 optgeom2xyz.py 转为xyz格式,从而可以在支持xyz格式的任何可视化软件里观看优化后的分子结构。例如待转换的文件名为filename.optgeom,则在命令行执行:(注意必须先设定环境变量$BDFHOME,或手动用BDF文件夹的路径替代下述命令里的$BDFHOME)
$BDFHOME/sbin/optgeom2xyz.py filename
即可在当前目录下得到filename.xyz。
备注
由以上步骤得到的.xyz文件里的坐标,虽然单位为Angstrom,但数值未必和.out文件里的坐标相同,这是正常现象,原因是两个文件的分子朝向以及坐标原点不同。同理,.optgeom文件里的坐标和.out文件里的坐标也并非简单的单位换算关系,而是可能还相差一个平动和一个转动。
最后顺便指出,当分子里有的键角接近或等于180度时,基于冗余内坐标的优化算法经常会出现数值不稳定性问题,导致优化无法继续进行。因此程序在产生冗余内坐标时,会尽量避免选取接近或等于180度的键角。但是即便如此,还是有可能有本来远小于180度的键角在优化过程中接近180度,导致数值不稳定问题,此时程序会自动重新构建冗余内坐标并自动重启优化,并输出如下信息:
Something wrong in getting dihedral!
This is probably because one or more angles have become linear.
--- Restarting optimizer ... (10 attempt(s) remaining) ---
由输出信息可知,程序总共允许优化器重启10次。一般情况下,仅需重启1~2次优化器即可成功优化得到结构,但极少数情况下,10次重启机会用完以后仍然会遇到键角接近180度的问题,此时程序报错退出:
bdfopt_bdf: fatal: the maximum number of restarts has been reached
Please check if your geometry makes sense!
此时用户应检查.optgeom文件里的当前坐标是否合理,如合理,则可改用DL-Find优化器,在直角坐标下进行优化,详情请参见 几何优化不收敛的解决方法 。
频率计算:\(\ce{CH3Cl}\) 在平衡结构下的谐振频率及热化学量的计算
结构优化收敛后,即可进行频率分析。准备以下输入文件:
$compass
title
CH3Cl freq
basis
def2-SV(P)
geometry
C -0.93557703 0.15971089 0.58828595
H -1.71170348 -0.52644336 0.21665897
H -1.26240747 1.20299703 0.46170050
H -0.72835075 -0.04452039 1.64971607
Cl 0.56770184 -0.09691413 -0.35697029
end geometry
$end
$bdfopt
hess
only
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
其中分子结构为上述结构优化任务得到的收敛的结构。注意我们在BDFOPT模块中添加了 hess only ,其中 hess 代表计算(数值)Hessian,而 only 的含义将在后续章节详述。程序将分子中的每个原子分别向x轴正方向、x轴负方向、y轴正方向、y轴负方向、z轴正方向、z轴负方向进行扰动,并计算扰动结构下的梯度,如:
Displacing atom 1 (+x)...
### [bdf_single_point] ### nstate= 1
Do not allow rotation to standard orientation.
BDFOPT run - details of gradient calculations will be written
into .out.tmp file.
...
### JOB TYPE = SCF ###
E_tot= -499.84157717
Converge= YES
### JOB TYPE = RESP_GSGRAD ###
Energy= -499.841577166026
1 0.0005433780 -0.0000683370 -0.0000066851
2 -0.0000516384 0.0000136326 -0.0000206081
3 -0.0001360377 0.0000872513 0.0000990006
4 -0.0003058645 0.0000115926 -0.0000775624
5 -0.0000498284 -0.0000354732 0.0000023346
备注
因扰动结构会破坏分子的点群对称性,所以即便用户输入的分子存在点群对称性,计算也会自动改为在C(1)群下进行。如果用户希望指定每个不可约表示下的轨道占据数,或希望计算某个特定不可约表示下的某个激发态的数值频率,则用户必须先单独做一个保持点群对称性的单点计算,根据单点计算的结果手动指认用户希望占据的轨道或希望计算的激发态对应于C(1)群下的哪个/哪些轨道或激发态,再根据指认结果撰写C(1)群下的数值频率计算输入文件。
若体系的原子数为N,则共需计算6N个梯度。然而实际上程序还会顺便计算未扰动的结构的梯度,以供用户检查前述结构优化是否确实已经收敛,因此程序实际共计算6N+1个梯度。最后程序通过有限差分方法得到体系的Hessian:
|--------------------------------------------------------------------------------|
Molecular Hessian - Numerical Hessian (BDFOPT)
1 2 3 4 5 6
1 0.5443095266 -0.0744293569 -0.0000240515 -0.0527420800 0.0127361607 -0.0209022664
2 -0.0744293569 0.3693301504 -0.0000259750 0.0124150102 -0.0755387479 0.0935518380
3 -0.0000240515 -0.0000259750 0.5717632089 -0.0213157291 0.0924260912 -0.2929392390
4 -0.0527420800 0.0124150102 -0.0213157291 0.0479752418 -0.0069459473 0.0239610358
5 0.0127361607 -0.0755387479 0.0924260912 -0.0069459473 0.0867377886 -0.0978524147
6 -0.0209022664 0.0935518380 -0.2929392390 0.0239610358 -0.0978524147 0.3068416997
7 -0.1367366097 0.0869338594 0.0987840786 0.0031968314 -0.0034098009 -0.0016497426
8 0.0869913627 -0.1185605401 -0.0945336434 -0.0070787068 0.0099076105 0.0045621064
9 0.0986508197 -0.0953400774 -0.1659434327 0.0163191407 -0.0140134399 -0.0166739137
10 -0.3054590932 0.0111756577 -0.0774713107 0.0016297078 0.0019657599 -0.0021771884
11 0.0112823039 -0.0407134661 0.0021058508 0.0106623780 0.0018506067 0.0005120364
12 -0.0775840113 0.0018141942 -0.0759448618 -0.0275602878 0.0006820252 -0.0059830018
13 -0.0486857506 -0.0362556088 0.0000641125 -0.0000787206 -0.0045253276 0.0011289985
14 -0.0360823429 -0.1334063062 0.0000148321 -0.0091074064 -0.0228930763 -0.0010993076
15 0.0001686252 0.0004961854 -0.0352553706 0.0084860406 0.0189117305 0.0079690194
7 8 9 10 11 12
1 -0.1367366097 0.0869913627 0.0986508197 -0.3054590932 0.0112823039 -0.0775840113
2 0.0869338594 -0.1185605401 -0.0953400774 0.0111756577 -0.0407134661 0.0018141942
3 0.0987840786 -0.0945336434 -0.1659434327 -0.0774713107 0.0021058508 -0.0759448618
4 0.0031968314 -0.0070787068 0.0163191407 0.0016297078 0.0106623780 -0.0275602878
5 -0.0034098009 0.0099076105 -0.0140134399 0.0019657599 0.0018506067 0.0006820252
6 -0.0016497426 0.0045621064 -0.0166739137 -0.0021771884 0.0005120364 -0.0059830018
7 0.1402213115 -0.0861503922 -0.1081442631 -0.0130805143 0.0143574755 0.0192323598
8 -0.0861503922 0.1322736798 0.1009922720 0.0016534140 0.0024111759 0.0011733340
9 -0.1081442631 0.1009922720 0.1688786678 -0.0038440081 0.0072277457 0.0091535975
10 -0.0130805143 0.0016534140 -0.0038440081 0.3186765202 -0.0079165663 0.0838593213
11 0.0143574755 0.0024111759 0.0072277457 -0.0079165663 0.0509206668 -0.0029665370
12 0.0192323598 0.0011733340 0.0091535975 0.0838593213 -0.0029665370 0.0707430980
13 0.0064620333 0.0044161973 -0.0031236007 -0.0026369496 -0.0283860480 0.0017966445
14 -0.0119743475 -0.0258901434 0.0013817613 -0.0066143965 -0.0145372292 -0.0006143935
15 -0.0078330845 -0.0126024853 0.0040383425 -0.0008566397 -0.0068931757 0.0018028482
13 14 15
1 -0.0486857506 -0.0360823429 0.0001686252
2 -0.0362556088 -0.1334063062 0.0004961854
3 0.0000641125 0.0000148321 -0.0352553706
4 -0.0000787206 -0.0091074064 0.0084860406
5 -0.0045253276 -0.0228930763 0.0189117305
6 0.0011289985 -0.0010993076 0.0079690194
7 0.0064620333 -0.0119743475 -0.0078330845
8 0.0044161973 -0.0258901434 -0.0126024853
9 -0.0031236007 0.0013817613 0.0040383425
10 -0.0026369496 -0.0066143965 -0.0008566397
11 -0.0283860480 -0.0145372292 -0.0068931757
12 0.0017966445 -0.0006143935 0.0018028482
13 0.0450796910 0.0642866688 0.0000350066
14 0.0642866688 0.1954779468 0.0000894464
15 0.0000350066 0.0000894464 0.0213253497
|--------------------------------------------------------------------------------|
其中第3N+1(3N+2、3N+3)行对应第N个原子的x(y、z)坐标,第3N+1(3N+2、3N+3)列同理。
接下来BDF调用UniMoVib程序进行频率和热力学量的计算。首先是振动所属不可约表示、振动频率、约化质量、力常数和简正模的结果:
************************************
*** Properties of Normal Modes ***
************************************
Results of vibrations:
Normal frequencies (cm^-1), reduced masses (AMU), force constants (mDyn/A)
1 2 3
Irreps A1 E E
Frequencies 733.9170 1020.5018 1021.2363
Reduced masses 7.2079 1.1701 1.1699
Force constants 2.2875 0.7179 0.7189
Atom ZA X Y Z X Y Z X Y Z
1 6 -0.21108 -0.57499 -0.00106 -0.04882 0.01679 0.10300 0.09664 -0.03546 0.05161
2 1 -0.13918 -0.40351 0.04884 -0.06700 -0.59986 -0.13376 -0.37214 -0.36766 -0.03443
3 1 -0.11370 -0.42014 -0.03047 0.26496 0.65294 -0.15254 -0.28591 -0.18743 -0.15504
4 1 -0.19549 -0.38777 -0.01079 0.05490 -0.14087 -0.24770 0.15594 0.73490 -0.07808
5 17 0.08533 0.23216 0.00014 0.00947 -0.00323 -0.01995 -0.01869 0.00699 -0.01000
其中各振动模式是按振动频率从小到大的顺序排列的,而虚频排在所有实频的前面,因此只需检查前几个频率,即可得知虚频的数目。接下来打印热化学分析结果:
*********************************************
*** Thermal Contributions to Energies ***
*********************************************
Molecular mass : 49.987388 AMU
Electronic total energy : -499.841576 Hartree
Scaling factor of Freq. : 1.000000
Tolerance of scaling : 0.000000 cm^-1
Rotational symmetry number: 3
The C3v point group is used to calculate rotational entropy.
Principal axes and moments of inertia in atomic units:
1 2 3
Eigenvalues -- 11.700793 137.571621 137.571665
X 0.345094 0.938568 -0.000000
Y 0.938568 -0.345094 -0.000000
Z 0.000000 0.000000 1.000000
Rotational temperatures 7.402388 0.629591 0.629591 Kelvin
Rot. constants A, B, C 5.144924 0.437588 0.437588 cm^-1
154.240933 13.118557 13.118553 GHz
# 1 Temperature = 298.15000 Kelvin Pressure = 1.00000 Atm
====================================================================================
Thermal correction energies Hartree kcal/mol
Zero-point Energy : 0.037519 23.543449
Thermal correction to Energy : 0.040539 25.438450
Thermal correction to Enthalpy : 0.041483 26.030936
Thermal correction to Gibbs Free Energy : 0.014881 9.338203
Sum of electronic and zero-point Energies : -499.804057
Sum of electronic and thermal Energies : -499.801038
Sum of electronic and thermal Enthalpies : -499.800093
Sum of electronic and thermal Free Energies: -499.826695
====================================================================================
用户可根据需要读取零点能、焓、Gibbs自由能等数据。注意以上所有热力学量是在以下各个假设下得到的:
频率校正因子为 1.0;
温度为 298.15 K;
压强为 1 atm;
电子态的简并度为1。
如用户的计算不属于以上情形,可以通过一系列关键词进行指定,如以下的写法代表频率校正因子为0.98,温度为373.15 K,压强为2 atm,电子态的简并度为2:
$bdfopt
hess
only
scale
0.98
temp
373.15
press
2.0
ndeg
2
$end
其中尤其需要注意的是电子态的简并度,对于非相对论或标量相对论计算,且电子态不存在空间简并性的情形,电子态的简并度等于自旋多重度(2S+1);对于存在空间简并性的电子态,还应乘上电子态的空间简并度,也即电子波函数的空间部分所属不可约表示的维数。至于考虑了旋轨耦合的相对论性计算(如TDDFT-SOC计算),则应将自旋多重度替换为相应旋量态的简并度(2J+1)。
在热化学数据之后,程序会检查梯度,根据内置的比较宽松的阈值,确认是否为驻点结构。与结构优化步骤不同,这里检测的是直角坐标梯度而不是内坐标梯度, 因为后者在个别情况下存在数值问题,容易导致误判。
有时因SCF不收敛或其他外在原因,导致频率计算中断,此时可在BDFOPT模块里加入 restarthess 关键词进行断点续算,节省计算时间,如:
$bdfopt
hess
only
restarthess
$end
此外值得注意的是,可以在同一个BDF任务里依次实现结构优化与频率分析(即所谓的opt+freq计算),而无需单独编写两个输入文件。为此只需将BDFOPT模块的输入改为:
$bdfopt
solver
1
hess
final
$end
其中final表示在结构优化成功结束后才进行数值Hessian计算;若结构优化不收敛,则程序直接报错退出,而不进行Hessian及频率、热力学量的计算。由此可以看出,前述的频率计算输入文件中的only,即为只进行频率计算而不进行结构优化之意。
备注
虽然opt+freq计算中的结构优化步骤支持在非C(1)点群下计算,但数值频率计算步骤仍然必须在C(1)群下计算。所以如果用户计算的分子具有点群对称性,且希望指定各个不可约表示的轨道占据数或指定优化某个特定不可约表示下的激发态,则必须先做结构优化,再根据前述步骤手动指认相应的轨道/激发态对应于C(1)群下的哪些轨道/激发态,再在C(1)群下进行数值频率计算,而不能直接做opt+freq计算。
过渡态结构优化:HCN/HNC异构反应的过渡态优化和频率计算
准备以下输入文件:
$compass
title
HCN <-> HNC transition state
basis
def2-SVP
geometry
C 0.00000000 0.00000000 0.00000000
N 0.00000000 0.00000000 1.14838000
H 1.58536000 0.00000000 1.14838000
end geometry
$end
$bdfopt
solver
1
hess
init+final
iopt
10
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
其中 iopt 10 表示优化过渡态。
无论是优化极小值点结构,还是优化过渡态,程序都必须在第一步结构优化之前产生一个初始的Hessian,以备后续结构优化步骤使用。一般而言,初始Hessian应当与初始结构下的精确Hessian定性符合,尤其是虚频数目必须一致。对于极小值点的优化,这个要求很容易满足,即便是分子力学级别的Hessian(所谓“模型Hessian”)也能做到和精确Hessian定性一致,因此此时程序以模型Hessian为初始Hessian,而无需计算精确Hessian。然而对于过渡态优化,模型Hessian一般不存在虚频,因此必须产生精确Hessian作为初始Hessian。以上输入文件的 hess init+final 即表示既产生初始Hessian以备过渡态优化需要(此Hessian因为不是在梯度为0的结构上计算的,频率及热化学量没有明确物理意义,因此仅计算Hessian而不做频率分析),又在结构优化收敛后再次进行Hessian计算,以得到频率分析结果。也可将 init+final 替换为 init ,即只产生初始Hessian,而结构优化收敛后不再次计算Hessian,但因过渡态优化(乃至所有结构优化任务)一般需要检验最终收敛的结构的虚频数目,因此不建议省略final关键词。
计算的输出与优化极小值点结构类似。最后频率分析时可以看到收敛的结构有且仅有一个虚频(-1104 \(\rm cm^{-1}\)):
Results of vibrations:
Normal frequencies (cm^-1), reduced masses (AMU), force constants (mDyn/A)
1 2 3
Irreps A' A' A'
Frequencies -1104.1414 2092.7239 2631.2601
Reduced masses 1.1680 11.9757 1.0591
Force constants -0.8389 30.9012 4.3205
Atom ZA X Y Z X Y Z X Y Z
1 6 0.04309 0.07860 0.00000 0.71560 0.09001 0.00000 -0.00274 -0.06631 0.00000
2 7 0.03452 -0.06617 0.00000 -0.62958 -0.08802 0.00000 0.00688 -0.01481 0.00000
3 1 -0.99304 -0.01621 0.00000 0.22954 0.15167 0.00000 -0.06313 0.99566 0.00000
代表确实找到了过渡态。
在以上计算中,初始Hessian的理论级别与过渡态优化的理论级别一致。因初始Hessian只需定性正确即可,实际计算中可以在另一个较低的级别下计算初始Hessian,再在较高理论级别下优化过渡态。仍以以上算例为例,假如我们想在HF/STO-3G级别下计算初始Hessian,而在B3LYP/def2-SVP级别下优化过渡态,可以按照以下步骤进行:
(1)准备以下输入文件,命名为 HCN-inithess.inp :
$compass
title
HCN <-> HNC transition state, initial Hessian
basis
STO-3G
geometry
C 0.00000000 0.00000000 0.00000000
N 0.00000000 0.00000000 1.14838000
H 1.58536000 0.00000000 1.14838000
end geometry
$end
$bdfopt
hess
only
$end
$xuanyuan
$end
$scf
rhf
$end
$resp
geom
$end
(2)用BDF运行该输入文件,得到Hessian文件 HCN-inithess.hess ;
(3)将 HCN-inithess.hess 复制或重命名为 HCN-optTS.hess ;
(4)准备以下输入文件,命名为 HCN-optTS.inp:
$compass
title
HCN <-> HNC transition state
basis
def2-SVP
geometry
C 0.00000000 0.00000000 0.00000000
N 0.00000000 0.00000000 1.14838000
H 1.58536000 0.00000000 1.14838000
end geometry
$end
$bdfopt
solver
1
hess
init+final
iopt
10
readhess
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
其中关键词 readhess 表示读取与该输入文件同名的hess文件(即HCN-optTS.hess)作为初始Hessian。注意尽管该输入文件不会重新计算初始Hessian,仍然需要写 hess init+final 而不是 hess final 。
(5)运行该输入文件即可。
用Dimer方法优化过渡态结构
为了获得过渡态的虚频振动模式,需要执行一次甚至多次的Hessian矩阵计算,这是优化过渡态的标准流程中最耗时的步骤。不过,也有一些过渡态优化方法只需要梯度,不需要计算Hessian矩阵,这就大大提高了计算效率以及量子化学方法的应用范围。 以下介绍的是Dimer方法 [74, 75, 76] 和CI-NEB方法 [77] 。
Dimer方法需要定义两个结构,称为像点(Image),两个像点的间距为一个固定的小值Delta,像点连线称为轴。 在Dimer计算过程中,对两个像点垂直于轴向的力进行最小化(称为旋转Dimer步骤),而在轴向的力进行最大化(称为平移Dimer步骤),最终收敛到过渡态结构。此时,轴向对应着虚频模式,而耗时的Hessian计算被巧妙地避开了。
注意
Dimer方法要调用DL-FIND外部库 [78] (
Solver=0),仅支持L-BFGS优化算法(IOpt=3)。由于DL-FIND与BDF默认的坐标转动有冲突,必须在
compass模块中加上关键词norotate禁止分子转动,或用nosymm关闭对称性;对于双原子和三原子分子,只能用nosymm。此冲突今后会解决。如果在过渡态优化后做频率计算,加上
hess=final。由于Dimer方法不需要Hessian,不要用init+final。
仍然取上一节的例子,加上关键词 dimer 和 nosymm (后者关闭对称性并禁止分子转动),优化方法 iopt 要从10改为默认的3(也可以不指定 iopt ),因为我们不需要计算Hessian。输入文件如下:
$compass
title
HCN <-> HNC transition state
basis
def2-SVP
geometry
C 0.00000000 0.00000000 0.00000000
N 0.00000000 0.00000000 1.14838000
H 1.58536000 0.00000000 1.14838000
end geometry
nosymm
$end
$bdfopt
solver
0
iopt
3
dimer
#hess
# final
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
经过14步优化结束:
Testing convergence of dimer midpoint in cycle 14
Energy 0.0000E+00 Target: 1.0000E-06 converged? yes
Max step 1.9375E-04 Target: 8.0000E-04 converged? yes component 4
RMS step 9.0577E-05 Target: 5.3333E-04 converged? yes
Max grad 6.9986E-06 Target: 2.0000E-04 converged? yes component 6
RMS grad 4.0401E-06 Target: 1.3333E-04 converged? yes
Converged!
得到的过渡态总能量为-93.22419648 Hartree,与上一节得到的能量-93.22419582 Hartree非常接近。
Summary printing of molecular geometry and gradient for this step
Atom Coord
C 0.381665 0.002621 0.138107
N -0.079657 -0.020912 1.233092
H 1.283352 0.018291 0.925561
State= 1
Energy= -93.22419612
Gradient=
C 0.00000523 0.00000093 -0.00000335
N 0.00000131 -0.00000022 0.00000700
H -0.00000655 -0.00000070 -0.00000365
如果修改Dimer方法的默认参数,可以把关键词 dimer 改为 Dimer-Block … End Dimer 输入块。其中的关键词参见BDFOPT模块的说明。
内禀反应坐标(IRC)计算
IRC(Intrinsic Reaction Coordinate)是量子化学研究化学反应的重要概念,它是质权坐标下连接势能面相邻两个极小点的能量最低路径,在不考虑热运动因素下,描述其化学过程中最理想的结构变化轨迹,对讨论微观化学过程至关重要,并且也是验证过渡态正确性的最决定性方法。
BDF的IRC计算是由IRC模块来实现的,使用的算法是支持笛卡尔坐标的Morokuma算法(J. Chem. Phys. 1977, 66, 2153), 该IRC计算需要过渡态结构的力常数,您需要提供优化收敛的过渡态结构 ts.inp 和该结构下的力常数信息 ts.hess ,为了加速IRC计算过程,您还需要提供该结构下收敛的分子轨道信息 ts.scforb 文件,这也意味着需要在BDF的输入文件中添加 guess readmo 这两行。以下对 BDFIRC 模块的输入文件格式举例进行介绍,并对输出文件进行解读。
计算IRC时,需要把 $IRC 模块的参数写在输入文件 3c2o5h.inp 的最前面,并且保留优化过渡态时使用的计算参数,即 $scf 和 $resp 模块需要严格保留。需要说明的是,你需要把ts对应的hess、scforb文件都改名为 3c2o5h.hess, 3c2o5h.scforb,以及把ts收敛的坐标写到 3c2o5h.inp 中。
IRC任务的高级输入为:
$irc
ircpts #反应路径的最大步数
50
ircdir #选择反应路径的方向
0
ircalpha #反应路径的步长参数
0.05
$end
# 下面的参数与计算TS结构时保持一致
$compass
Title
Irc4bdf
Geometry
C -0.81981975 1.01964884 0.22750818
C 0.62889615 1.02275098 -0.13495924
O 1.14639042 -0.35161068 0.02899058
C 0.09835734 -1.20263633 0.05869588
O -1.03508512 -0.71305587 -0.26218679
H -1.52425628 1.52979576 -0.43070061
H -1.07734340 1.04483316 1.29117725
H 0.79223623 1.32207879 -1.18212528
H 1.25263913 1.63815017 0.52777758
H 0.22167944 -2.05610649 0.75197182
End geometry
Basis
CC-PVDZ
$end
$xuanyuan
$end
$scf
uks
guess
readmo
dft
GB3LYP
charge
0
spinmulti
2
mpec+cosx
molden
$end
$resp
Geom
$end
计算结果分析
运行完IRC任务后,BDF会额外生成 3c2o5h.irc 文件和 3c2o5h.trj 文件。
3c2o5h.irc文件保留了每一步计算的信息;3c2o5h.trj文件保留了每一步的轨迹文件。
其中 3c2o5h.irc 会首先给出一些基本的用户设置信息,
IRC wrapper for BDF - version 2023A
Using BDF from: $BDFHOME/sbin/bdfdrv.py
Parameters for this run:
Algorithm: 1
N. Points: 50
Grad. Tol.: 0.0001
Hessian: c3o2h5.hess
Mode: 0
Direction: 1
Alpha: 0.0500
Delta: 0.0500
Damp Factor: 0.0500
Damp Update: 0
Max. Displ.: 0.0100
Guess: c3o2h5.TS.scforb
接下来会有计算的每一帧结构的能量以及RMS Grad,
------------------------------------------------------------------------
Pt. Energy RMS Grad. Damp
-------------------------------------------------------------------------
@ 1 -267.675550488 0.01427 5.00e-02
@ 2 -267.679192880 0.00232 5.00e-02
@ 3 -267.681201395 0.01348 5.00e-02
@ 4 -267.690625817 0.01357 5.00e-02
@ 5 -267.696989174 0.01006 5.00e-02
@ 6 -267.699945911 0.00574 5.00e-02
@ 7 -267.701148839 0.00394 5.00e-02
@ 8 -267.701644838 0.00262 5.00e-02
@ 9 -267.701959150 0.00243 5.00e-02
@ 10 -267.702145221 0.00170 5.00e-02
@ 11 -267.702350215 0.00189 5.00e-02
@ 12 -267.702476410 0.00117 5.00e-02
@ 13 -267.702602274 0.00145 5.00e-02
@ 14 -267.702713773 0.00096 5.00e-02
@ 15 -267.702843816 0.00133 5.00e-02
@ 16 -267.702921941 0.00113 5.00e-02
@ 17 -267.702997038 0.00077 5.00e-02
最后正常收敛的话会出现
----------------------------------------------
-- ENERGY INCREASED --
-- GEOMETRY MIGHT BE --
-- VERY CLOSE TO A MINIMUM --
-- --
-- IRC CALCULATION TERMINATED! --
----------------------------------------------
另外 3c2o5h.trj 就是把每一步的轨迹输出,形式如下,
10
IRC for BDF-irc-f point 1 E= -267.6755505
C -0.774450 1.005021 0.227507
C 0.623378 1.023651 -0.134433
O 1.142071 -0.346726 0.029851
C 0.099686 -1.204880 0.058039
O -1.040129 -0.707532 -0.261197
H -1.538885 1.536311 -0.439412
H -1.084614 1.045208 1.295915
H 0.789098 1.321574 -1.178911
H 1.246292 1.636770 0.526219
H 0.221239 -2.055548 0.752570
10
IRC for BDF-irc-f point 2 E= -267.6791929
C -0.806848 1.013333 0.225962
C 0.635583 1.022502 -0.136684
O 1.144366 -0.348838 0.029978
C 0.099054 -1.205298 0.056237
O -1.037689 -0.705204 -0.259469
H -1.515348 1.520972 -0.422025
H -1.076532 1.043033 1.285840
H 0.789437 1.322192 -1.180942
H 1.248393 1.638410 0.527357
H 0.220724 -2.055404 0.753891
提示
使用IRC模块需要用户安装好numpy;
用户可以把得到的坐标文件输入到Device Studio中,查看轨迹的变化情况,DS平台待更新此功能。
用CI-NEB方法计算最低能量路径和优化过渡态
与原始的拉橡皮筋(Nudged Elastic Band;NEB)方法不同,CI-NEB方法在能量最高点增加了像点爬升(Climbing Image;CI)处理步骤,因此不仅能得到更准确的最低能量(反应)路径,同时还能得到过渡态结构 [77] 。
仍然取上一节HCN异构反应的例子,注意事项参见前面的Dimer方法。
CI-NEB计算需要提供两个端点的坐标,其中第一个端点(这里取反应物HCN)的初始结构在 Compass 模块提供,由于直线形结构不易处理,加了一点扰动。
第二个端点是弯曲结构(经过CI-NEB优化后成为HNC异构体),在 Geometry2 … End Geometry2 输入块提供。
两套坐标的原子顺序必须一致。输入文件如下:
$compass
basis-block
def2-SVP
end basis
geometry
C 0.0200000 0.0000000 0.0000000
N 0.0000000 -1.1400000 0.0000000
H 0.0000000 1.0500000 0.0000000
end geometry
nosymm
$end
$bdfopt
solver
0
iopt
3
neb-block
crude
nebmode
0
nimage
3
end neb
geometry2
C 0.0000000 0.0000000 0.0000000
N -1.1500000 0.2300000 0.0000000
H -1.6100000 1.1100000 0.0000000
end geometry2
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
由于CI-NEB方法的中间像点数越多计算越慢,且增加结构不收敛的几率,因此不建议用太多的中间像点,建议在3至7之间。
如果只关心过渡态,也可以尝试用更少的中间像点,例如1,但对本例不可行,因为反应物和产物是线型结构,而中间像点是弯曲结构,
导致二者的梯度矢量重叠太小,影响结构收敛。
本例用了3个中间像点,由 Nimage 定义,并用 Crude 降低收敛精度,同时对反应物和产物做能量最小化( Nebmode = 0;默认固定不优化)。
除了 Nimage 指定的3个中间像点,还有必须要算的3个像点,因此总像点数为6。其中,1、5像点对应两个端点(即反应物和产物),2、3、4为反应路径上的中间像点。
这5个像点优化到一定程度时,会创建用于爬升步骤的像点6,它最终会优化到过渡态。
经过31步结构优化后,CI-NEB方法找到了最低能量路径:
Testing convergence of NEB climbing image in cycle 31
Energy 7.1900E-07 Target: 4.0000E-05 converged? yes
Max step 1.1193E-03 Target: 5.3333E-03 converged? yes component 8
RMS step 6.5514E-04 Target: 3.5556E-03 converged? yes
Max grad 7.4900E-05 Target: 1.3333E-03 converged? yes component 5
RMS grad 3.6435E-05 Target: 8.8889E-04 converged? yes
Convergence reached
输出文件往前翻,可以看到各个像点(包括反应物、产物、过渡态)的能量总结报告:
NEB Report
Energy F_tang F_perp Dist Angle 1-3 Ang 1-2 Sum
Img 1 -93.3003651 0.00000 0.00000 1.17248 0.00 0.00 63.25 frozen
Img 2 -93.2804319 0.00160 0.00059 1.01235 63.25 86.25 94.29 frozen
Img 3 -93.2270244 -0.00167 0.00049 1.17963 31.04 77.08 80.27 frozen
Img 4 -93.2512597 -0.00248 0.00075 1.42718 49.23 0.00 49.23 frozen
Img 5 -93.2785849 0.00000 0.00000 0.00000 0.00 0.00 0.00 frozen
Cimg 3 -93.2241949 0.00010 0.00007 0.21264 0.00 0.00 0.00
在上面的表格中, Energy 列给出了反应路径上每个像点的能量,其中最后一个 Cimg 表示爬升像点,也就是过渡态, 并且标记了离它最近的像点(本例是3号像点)。 F_tang 列和 F_perp 列给出了每个像点在平行路径和垂直路径方向的受力,原则上应当接近零。 Dist 列、 Angle 列、、 1-3 Ang 列、 1-2 Sum 列给出了路径的特性,分别当前像点为到下一个像点的距离(可以看到NEB的像点经过优化后,不再是等间隔的), 当前像点与上一个像点的角度,下一个像点与上一个像点的角度,以及当前像点和下一个像点的角度之和。 把 Dist 列的数据累加作为横轴,能量作为纵轴,可以绘制NEB反应坐标能量图(这些数据可以在单独的文件nebinfo中找到)。
Cimg 这一行给出的过渡态总能量是-93.2241949 Hartree(DL-FIND最终打印的 Final converged energy 也是这个能量),与之前Dimer方法优化得到的过渡态总能量-93.22419648 Hartree非常接近。
过渡态的直角坐标可以在能量数据之前找到(原子单位),同时也打印在CI-NEB保存的文本文件 neb_0006.xyz (因为过渡态在本例中是第六个像点)的末尾,单位是埃。 其余5个像点的直角坐标保存在文本文件nebpath.xyz中(单位:埃)。 如果必要,也可以用前面介绍的方法对过渡态结构做更严格的优化,这要比在CI-NEB计算中直接用严格收敛标准更加高效。
把每一步优化的像点能量提取出来,画NEB轨迹图如下。作为演示,横轴坐标取自最后一步,但实际上每一步的横轴坐标都会有一些变化。
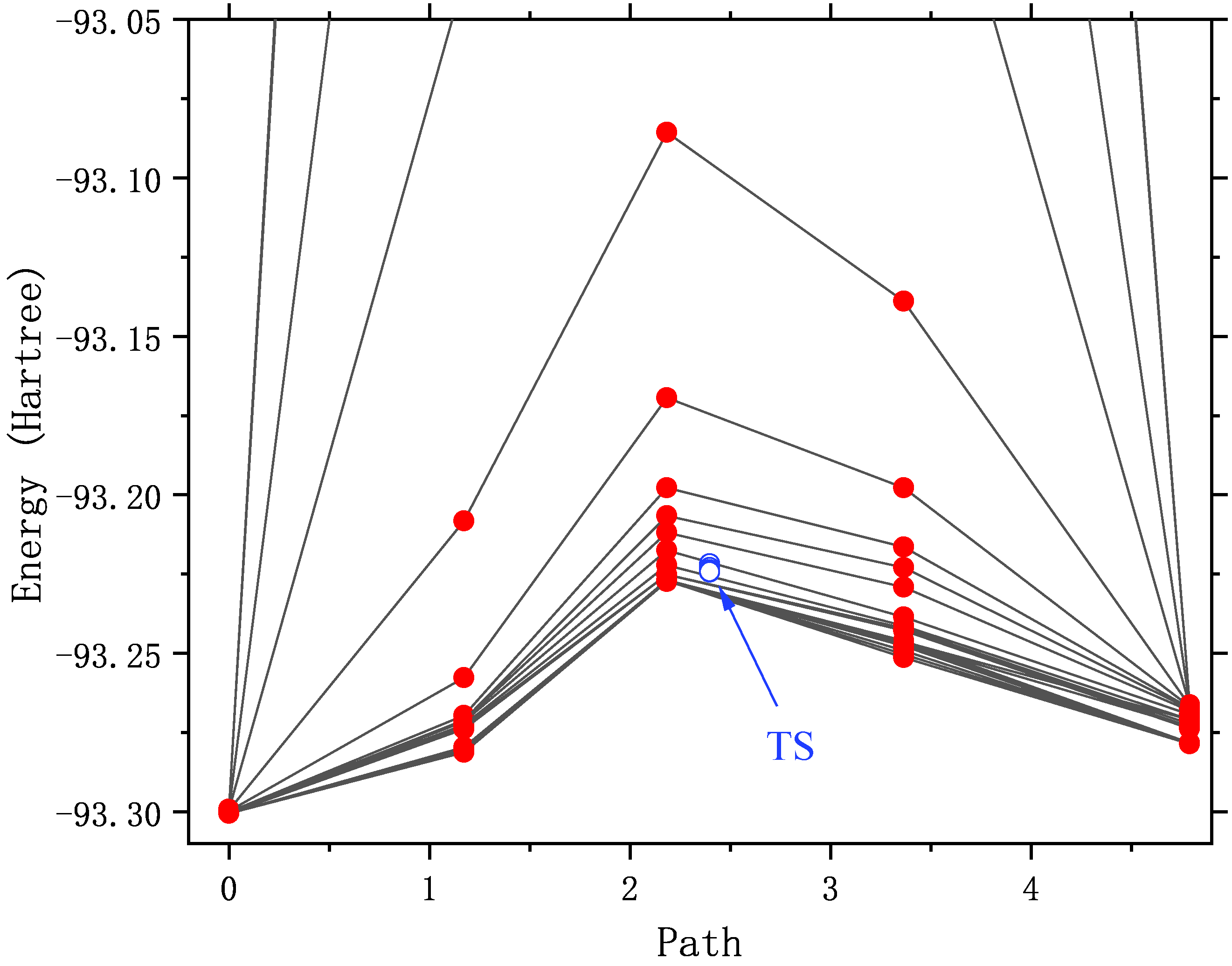
可见随着优化,路径的能量逐渐降低,直至收敛。或许有人注意到了,2至4号像点在最初几轮结构优化中的能量非常高(超出显示范围), 说明这些点的初始结构不太合理。例如,在3号像点的初始结构中,C-N键长仅有0.5埃!不合理的结构不仅会阻碍结构收敛,还破坏SCF收敛, 或者收敛到我们不想要的激发态上。
CI-NEB计算经常不收敛。有以下处理方法:
提取能量最高像点的结构,或者爬升像点的结构,改用之前介绍的过渡态优化方法进行计算。
提取能量最高的两个像点的结构(例如本算例的3、4)作为初始结构,重新做CI-NEB优化,但是此时
Nebmode要改为1或2,因为它们已不再是反应物、产物或中间体,做能量最小化没有意义。取结构优化最后一步的两个端点结构,以及部分或全部中间像点结构(来自数据文件nebpath.xyz),作为初始结构,重新做CI-NEB优化。输入文件如下。 在本例中,两个端点的结构已经接近收敛( F_tang 和 F_perp 都非常小),为了提高计算速度,结构保持冻结(
Nebmode=2)。
$compass
basis-block
def2-SVP
end basis
geometry
# geom of image 1 (endpoint 1)
C 0.0094403 -0.0045178 0.0000000
N 0.0051489 -1.1595576 0.0000000
H 0.0054108 1.0740754 0.0000000
end geometry
norotate
$end
$bdfopt
solver
0
iopt
3
Trust
0.02
neb-block
crude
nebmode
2
nimage
3
end neb
nframe
4
geometry2
# geom of image 2
C 0.2822075 -0.0905533 0.0000000
N -0.4636856 -0.9729686 0.0000000
H 0.2014782 0.9735219 0.0000000
# geom of image 3
C 0.5703159 -0.2134900 0.0000000
N -0.5233808 -0.6609221 0.0000000
H -0.0269352 0.7844121 0.0000000
# geom of image 4
C 0.7857794 -0.5068651 0.0000000
N -0.3940425 -0.3160241 0.0000000
H -0.3717369 0.7328892 0.0000000
# geom of image 5 (endpoint 2)
C 0.5798873 -0.9890158 0.0000000
N -0.0251869 0.0162146 0.0000000
H -0.5347005 0.8828012 0.0000000
end geometry2
$end
$xuanyuan
$end
$scf
rks
dft
b3lyp
$end
$resp
geom
$end
这里用了一个小技巧:自动生成的中间像点坐标中,z方向坐标可能非零,三原子分子情况下会导致 Norotate 关键词与对称性程序发生冲突,
因此前面不得不用 Nosymm 关闭对称性。现在既然已经有了定性正确的像点坐标,我们可以把这些坐标在z方向的小值清零,
再把 Nosymm 改为 Norotate ,这样就可以利用Cs对称性加快计算。
重新画NEB轨迹,如下图所示。由于中间像点使用了较好的初始结构,在优化前几步的能量已经合理了。
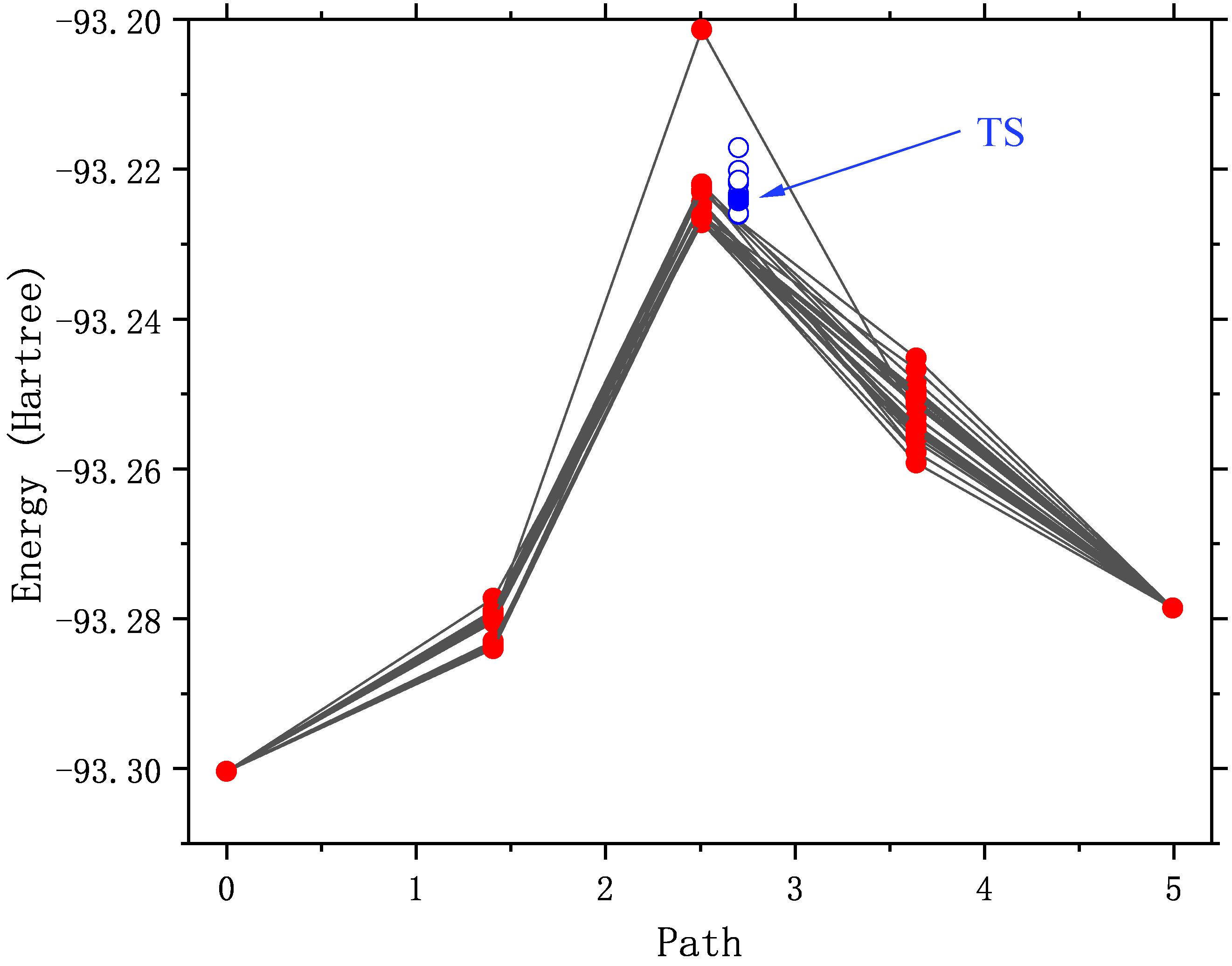
自旋混合态的结构优化:ZnS分子
双原子分子ZnS的基态是闭壳层的 \(X^1\Sigma^+\) ,键长2.05埃;在11 kcal/mol以上有第一激发态 \(^3\Pi\) , 与基态在2.4埃附近发生交叉 [79] 。激发态的 \(^3\Pi_{0+}\) 分量与基态存在相互作用, 可能影响基态的键长。
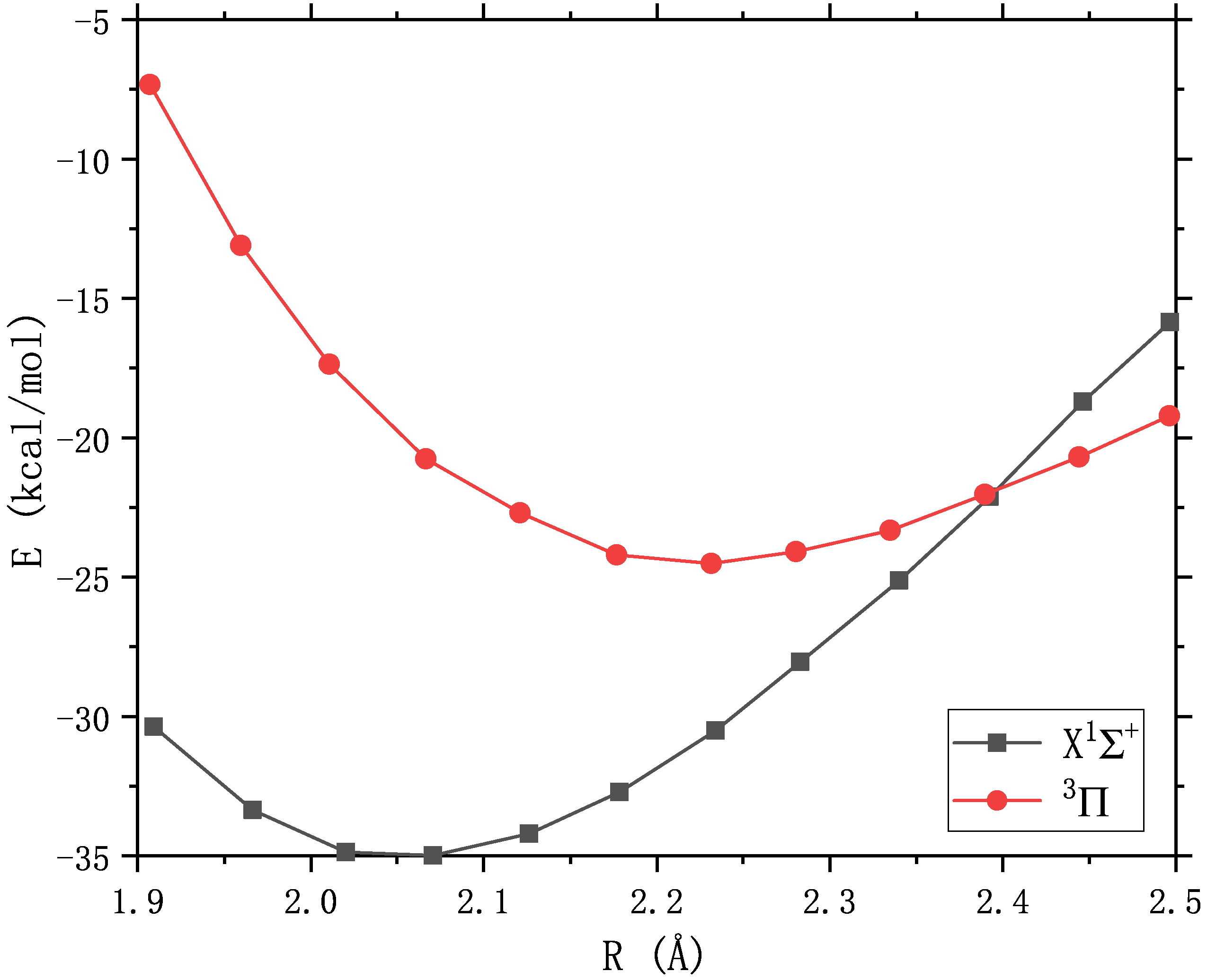
如果对精度要求不高,可以用Truhlar等人建议的自旋轨道模型哈密顿 [80] 模拟两个自旋态之间的旋轨耦合, 考虑 \(^3\Pi_{0+}\) 对基态的影响。 输入文件如下。其中,基态用RKS完成,最低三重激发态用UKS完成。输入文件中有以下几点需要注意:
备注
两态混合计算的选项是
2soc(类似有3soc、4soc等)。一般来说,这两个自旋态需要有 不同的自旋多重度 ,除非理论计算证明两个相同自旋的态之间也存在强SOC相互作用(例如氮族原子的 \(^2D_u\) 和 \(^2P_u\) )。这里设置的旋轨耦合常数经验值400 \(\rm cm^{-1}\) 恰好是程序默认值,因此可以省略不写。
通过
solver= 1指定BDF自带优化器。也可以用DL-Find优化器,但是一般会慢一些。两个自旋态的能量、梯度要分别保存到
$BDFTASK.egrad.1和$BDFTASK.egrad.2文件。 至于哪个态规定为1号或2号,完全由用户决定,不影响最终结果。在BDF结构优化过程中,默认用上一步保存的SCF轨道作为当前SCF步骤的初猜,以获得最快的SCF收敛。由于两个SCF计算使用的SCF初猜轨道不同, 需要把它们分别备份为
$BDFTASK.scforb.1和$BDFTASK.scforb.2。然而当首次用它们覆盖$BDFTASK.scforb时,由于尚未进行SCF计算, 这两个文件不存在导致复制出错,BDF发现后会停止计算。为了屏蔽掉复制出错的信息,需要在复制命令的末尾加上2>/dev/null || :。最低三重激发态也可以用TDDFT通过自旋翻转计算,需要在
$tddft和$resp中加入一些额外的关键词(参见 TDDFT相关章节 )。 不过TDDFT不能很好描述电荷转移态(ZnS就属于这种情况),这里不采用。
$COMPASS
Title
two-state calculation of ZnS
Basis
lanl2dz
Geometry
Zn 0.0 0.0 0.0
S 0.0 0.0 2.05
END geometry
$END
$bdfopt
solver
1
multistate
2soc 400
$end
$xuanyuan
$end
%cp $BDF_WORKDIR/$BDFTASK.scforb.1 $BDF_WORKDIR/$BDFTASK.scforb 2>/dev/null || :
$SCF
rks
dft
pbe0
charge
0
spinmulti
1
$END
%cp $BDF_WORKDIR/$BDFTASK.scforb $BDF_WORKDIR/$BDFTASK.scforb.1
$resp
geom
$end
%cp $BDF_WORKDIR/$BDFTASK.egrad1 $BDF_WORKDIR/$BDFTASK.egrad.1
%cp $BDF_WORKDIR/$BDFTASK.scforb.2 $BDF_WORKDIR/$BDFTASK.scforb 2>/dev/null || :
$SCF
uks
dft
pbe0
charge
0
spinmulti
3
$END
%cp $BDF_WORKDIR/$BDFTASK.scforb $BDF_WORKDIR/$BDFTASK.scforb.2
$resp
geom
$end
%cp $BDF_WORKDIR/$BDFTASK.egrad1 $BDF_WORKDIR/$BDFTASK.egrad.2
计算结束后,优化的自旋混合基态键长是2.1485埃,比纯单重基态的键长2.1480埃(这个值远远大于高精度理论值2.05埃,是因为本算例采用的基组太小)略长一些, 说明 \(^3\Pi_{0+}\) 通过旋轨耦合作用把基态的键长拉长。最后一步优化的输出信息显示, \(^3\Pi_{0+}\) 在自旋混合基态中占了0.2%。
Multi-state calculation
-----------------------
Mixed-spin states by 2 scalar states.
Chi = 400.0 cm^-1 is used to constuct the SO model Hamiltonian.
/tmp/zouwl/BDF-1/test.egrad.1
E= -75.49718339
/tmp/zouwl/BDF-1/test.egrad.2
E= -75.46038704
Energies and weights of mixed-spin states:
------------------------------------------------------------------
No. E(mix) Weights
------------------------------------------------------------------
1 -75.49727344 99.8% 0.2%
2 -75.46029699 0.2% 99.8%
------------------------------------------------------------------
除了优化自旋混合基态的结构,还可以计算它的振动频率,为此需要把两个自旋态的Hessian分别保存到 $BDFTASK.hess.1 和 $BDFTASK.hess.2 文件。
如果仅在优化的结构上计算频率,和上面结构优化的输入类似,只需要把
solver= 1 改为hess=only,并把备份梯度文件$BDFTASK.egrad1改为备份Hessian文件$BDFTASK.hess。在做结构优化+频率计算时,输入要做额外修改。这是因为优化过程中不存在Hessian文件,而频率计算过程中不存在梯度文件,必须用
2>/dev/null || :屏蔽掉复制出错的信息。能够正常运行的输入文件如下:
$COMPASS
Title
two-state calculation of ZnS
Basis
lanl2dz
Geometry
Zn 0.0 0.0 0.0
S 0.0 0.0 2.05
END geometry
$END
$bdfopt
solver
1
multistate
2soc 400
hess
final
$end
$xuanyuan
$end
%cp $BDF_WORKDIR/$BDFTASK.scforb.1 $BDF_WORKDIR/$BDFTASK.scforb 2>/dev/null || :
$SCF
rks
dft
pbe0
charge
0
spinmulti
1
$END
%cp $BDF_WORKDIR/$BDFTASK.scforb $BDF_WORKDIR/$BDFTASK.scforb.1
$resp
geom
$end
%cp $BDF_WORKDIR/$BDFTASK.egrad1 $BDF_WORKDIR/$BDFTASK.egrad.1 2>/dev/null || :
%cp $BDF_WORKDIR/$BDFTASK.hess $BDF_WORKDIR/$BDFTASK.hess.1 2>/dev/null || :
%cp $BDF_WORKDIR/$BDFTASK.scforb.2 $BDF_WORKDIR/$BDFTASK.scforb 2>/dev/null || :
$SCF
uks
dft
pbe0
charge
0
spinmulti
3
$END
%cp $BDF_WORKDIR/$BDFTASK.scforb $BDF_WORKDIR/$BDFTASK.scforb.2
$resp
geom
$end
%cp $BDF_WORKDIR/$BDFTASK.egrad1 $BDF_WORKDIR/$BDFTASK.egrad.2 2>/dev/null || :
%cp $BDF_WORKDIR/$BDFTASK.hess $BDF_WORKDIR/$BDFTASK.hess.2 2>/dev/null || :
多态混合模型的主要用途是研究多态反应,优化自旋混合态的反应物,中间体,产物,过渡态, 以及反应路径。相比于MECP优化,它能提供更多信息(例如,如果MECP导致新的过渡态,多态混合模型可以估算MECP附近的振动频率和热化学量)。 当原子不太重的情况下(5d之前),多态混合模型比严格考虑旋轨耦合的二分量或四分量相对论方法有更多优势。
限制性结构优化
BDF还支持在结构优化中限制一个或多个内坐标的值,方法是在BDFOPT模块中加入constrain关键词。constrain关键词后的第一行为一个整数(以下称为N),表示总的限制数目;第2行到第N+1行定义每个限制。例如以下输入表示在结构优化时限制第2个原子和第5个原子之间的距离(这两个原子之间不一定需要有化学键):
$bdfopt
solver
1
constrain
1
2 5
$end
以下输入表示在结构优化时限制第1个原子和第2个原子之间的距离,同时还限制第2、第5、第10个原子形成的键角(同样地,不要求第2、第5个原子,或第5、第10个原子之间有化学键):
$bdfopt
solver
1
constrain
2
1 2
2 5 10
$end
以下输入表示在结构优化时限制第5、第10、第15、第20个原子之间的二面角,同时还限制第10、第15、第20、第25个原子之间的二面角:
$bdfopt
solver
1
constrain
2
5 10 15 20
10 15 20 25
$end
备注
即使分子坐标是以直角坐标而非内坐标的形式输入的,BDF仍然可以对内坐标做限制性优化。
当需要同时冻结多个原子(例如用团簇模型研究表面催化反应,欲冻结一部分催化剂原子)时,虽仍然可以穷尽这些原子之间的所有键长、键角、二面角并一一冻结,但是当需要冻结的原子数较多时,这样做比较麻烦、易错。因此BDF还支持冻结原子的笛卡尔坐标的功能,方法是使用frozen关键字。例如:
$bdfopt
...
frozen
3 # number of atoms to be frozen
2 -1
5 -1
10 -1
$end
表示冻结第2、5、10号原子。当使用DL-Find优化器(即solver=0)时,还可将-1替换为其他的数字,以只冻结该原子x、y、z坐标中的一个或两个:
0: free (default)
-1: frozen
-2: x frozen only
-3: y frozen only
-4: z frozen only
-23: x and y frozen
-24: x and z frozen
-34: y and z frozen
例如
$bdfopt
...
frozen
4 # number of atoms to be frozen
3 -1
4 -1
5 -1
6 -4
$end
即为冻结3~5号原子的笛卡尔坐标,以及6号原子的z坐标,但6号原子在x、y方向上仍可自由移动。
备注
(1)程序冻结的是用户指定的各原子之间的相对笛卡尔坐标,原子的绝对笛卡尔坐标仍可能因为分子标准取向的变化而变化; (2)同一个计算可以既冻结任意多的笛卡尔坐标,也冻结任意多的内坐标。
对于冻结内坐标的计算,程序还支持将内坐标冻结为某个和初始结构不同的值。例如以下输入文件,在M06-2X/6-31+G(d,p)/SMD(water)级别下优化环氧乙烷的结构,但限制其中一根C-O键长为2.0埃:
$compass
Geometry
C 0.00000000 0.70678098 -0.40492819
C 0.00000000 -0.70678098 -0.40492819
O 0.00000000 0.00000000 0.95133348
H 0.86041653 1.24388179 -0.74567167
H -0.86041653 1.24388179 -0.74567167
H 0.86041653 -1.24388179 -0.74567167
H -0.86041653 -1.24388179 -0.74567167
End Geometry
Basis
6-31+G(d,p)
MPEC+COSX
$end
$bdfopt
Solver
1
constraint
1 # number of constraints
2 3 = 2.0 # constrain the distance of atom 2 and atom 3 at 2.0 Angstrom
$end
$xuanyuan
$end
$scf
RKS
dft
M062X
solmodel
SMD
solvent
water
$end
$resp
geom
$end
初始结构中,两根C-O键的键长均为1.53埃,但优化收敛后,可以发现被冻结的C-O键的键长刚好为2.00埃(而不是1.53埃),另一根没有冻结的C-O键长则被优化为1.43埃:
|******************************************************************************|
Redundant internal coordinates on Angstrom/Degree
Name Definition Value Constraint
R1 1 2 1.4907 No
R2 1 3 1.4332 No
R3 1 4 1.0917 No
R4 1 5 1.0917 No
R5 2 3 2.0000 Yes
R6 2 6 1.0845 No
R7 2 7 1.0845 No
A1 2 1 3 86.29 No
...
同一个计算冻结的坐标中,可以只给一部分赋值,其余坐标自动沿用初始结构中的值。例如以下输入是合法的,表示冻结原子1、2、5的笛卡尔坐标,且冻结原子5-原子6-原子8的键角,以及原子11-原子12-原子13-原子14的二面角。其中除了原子5-原子6-原子8的键角被冻结为60度以外,其他几个被冻结的坐标的取值均与用户给定的初始结构一致,例如假如初始结构中原子11-原子12-原子13-原子14的二面角为120度,则在之后的结构优化中原子11-原子12-原子13-原子14的二面角始终为120度:
$bdfopt
...
solver
1
frozen
3
1 -1
2 -1
5 -1
constrain
2
5 6 8 = 60.
11 12 13 14
$end
备注
程序只支持设定被冻结的键长、键角、二面角值,而不支持在冻结笛卡尔坐标时设定被冻结的原子的笛卡尔坐标值。
当用户同时冻结多个内坐标并赋值时,用户需确认其冻结的内坐标值彼此自洽。作为内坐标不自洽的例子,考虑以下输入:
$bdfopt
Solver
1
constraint
3
1 2 = 1.0
1 3 = 2.0
2 3 = 4.0
$end
显然,这三个键长限制条件不能同时满足,因为无法由键长1埃、2埃、4埃的三根键构成一个三角形。程序发现无法同时满足三个限制条件后,打印警告信息:
q2c_coord_calc: warning: the 1-th constraint cannot be enforced, error = 0.204E+00
Check if the input constraints are mutually contradictory, or numerically ill-posed!
q2c_coord_calc: warning: the 2-th constraint cannot be enforced, error = 0.200E+00
Check if the input constraints are mutually contradictory, or numerically ill-posed!
q2c_coord_calc: warning: the 3-th constraint cannot be enforced, error = -0.149E+01
Check if the input constraints are mutually contradictory, or numerically ill-posed!
最后因多次重启优化器仍然无法解决该问题,程序报错退出。
备注
以上算例中,同时满足各个内坐标限制条件是数学上不可能的。有时虽然同时满足各个限制条件在数学上可能,但初始结构离满足限制条件的结构太远,此时程序仍然可能找不到同时满足所有限制条件的结构,并打印警告或报错退出。
激发态结构优化
BDF程序除优化基态结构外,还可优化激发态结构,具体请参见 TDDFT相关章节 ,此处不再赘述。
QM/MM结构优化
BDF还可以用QM/MM组合方法进行结构优化,但与纯QM结构优化不同的是,QM/MM结构优化不能使用BDFOPT模块完成,而必须借助pDynamo程序自带的结构优化函数。具体请参见 QM/MM相关章节 ,此处不再赘述。
自动消除虚频
不管是优化极小值点结构还是优化过渡态,都经常会遇到优化收敛的结构的虚频数目与预期不符的问题,具体可分为3类:(1)优化极小值点收敛的结构有虚频;(2)优化过渡态收敛的结构的虚频多于1个;(3)优化过渡态收敛的结构没有虚频。对于(1)、(2)两类情况,BDF可以自动消除多余的虚频,为此需要在BDFOPT模块的输入里添加 rmimag (或 removeimag )关键词;该关键词对于(3)的情况也有一定作用,即在优化过渡态结果没有虚频时可以在附近寻找有一个虚频的结构,但成功率较低。例如以下输入表示,优化极小值点结构,然后做一个频率计算,如果没有虚频则结束计算;如果有虚频则自动将分子结构沿着绝对值最大的虚频对应的振动模的方向扰动,然后继续优化,优化收敛后再做一次频率计算验证虚频有没有消掉,如此反复直至所有虚频完全消掉,或计算了10次频率仍然没办法消掉所有虚频为止:
$bdfopt
solver
1
rmimag
$end
以下输入和上述输入的效果类似,区别在于会对最后一次算出的Hessian做完整的频率分析和热化学分析:
$bdfopt
solver
1
rmimag
hess
final
$end
以下输入表示,优化过渡态结构(在优化开始前先做一个频率计算,来提供结构优化的初始Hessian),然后做一个频率计算,如果恰有1个虚频则结束计算。如果虚频数目大于1,则自动将分子结构沿着绝对值第二大的虚频的方向扰动,然后继续优化,优化收敛后再做个频率计算验证多余的虚频有没有消掉,如此反复直至虚频数目等于1。如果虚频数目等于0,则自动尝试在附近寻找虚频数目等于1的结构,优化收敛后同样重新计算频率,验证虚频数目,如此反复直至虚频数目等于1:
$bdfopt
solver
1
rmimag
hess
init # calculate initial Hessian. If a thermochemistry analysis on the final Hessian is desired, change “init” to “init+final”
iopt
10 # transition state optimization
$end
以下是一个完整的算例,该算例在HFLYP/6-31G(d)水平下优化了 \(\ce{ClF3}\) 的平衡结构:
$compass
title
ClF3
basis
6-31G(d)
geometry
Cl 0.000000 0.000000 0.000000
F -2.966870 0.000000 0.000000
F 1.483435 2.569385 0.000000
F 1.483435 -2.569385 0.000000
end geometry
unit
bohr
nosymm
$end
$bdfopt
solver
1
rmimag
hess
final
$end
$xuanyuan
$end
$scf
rks
dft
HFLYP
$end
$resp
geom
$end
初始结构符合 \(\rm D_{3h}\) 对称性,但因为预期优化收敛的结构可能存在虚频,在 compass 模块里用 nosymm 关键字指定在 \(\rm C_{1}\) 群下计算。程序首先收敛到 \(\rm D_{3h}\) 点群下的极小值点:
|******************************************************************************|
Redundant internal coordinates on Angstrom/Degree
Name Definition Value Constraint
R1 1 2 1.6666 No
R2 1 3 1.6667 No
R3 1 4 1.6667 No
A1 2 1 3 119.99 No
A2 2 1 4 119.99 No
A3 3 1 4 120.02 No
D1 4 1 3 2 179.97 No
D2 2 1 4 3 179.97 No
D3 3 1 4 2 -179.97 No
|******************************************************************************|
接着重启结构优化器:
--- Restarting optimizer ... (10 attempt(s) remaining) ---
接下来程序会进行一个数值Hessian计算,发现该结构有两个虚频:
Warning: the number of imaginary frequencies, 2, is different from the desired number, 0!
因此程序对该结构进行扰动,并继续优化,以期消除虚频。其中因一个F-Cl-F键角接近180°,需要重新构建冗余内坐标,导致结构优化器再次重启。最后收敛得到属于 \(\rm C_{2v}\) 点群、呈T字形的结构:
|******************************************************************************|
Redundant internal coordinates on Angstrom/Degree
Name Definition Value Constraint
R1 1 2 1.5587 No
R2 1 3 1.6470 No
R3 1 4 1.6470 No
R4 2 4 2.1859 No
A1 2 1 3 85.95 No
A2 2 1 4 85.94 No
|******************************************************************************|
最后第3次重启结构优化器,经过Hessian计算确认,该结构没有虚频,即一开始的两个虚频已经消除。此时整个计算宣告收敛:
*************************************** Properties of Normal Modes ***************************************
Results of vibrations:
Normal frequencies (cm^-1), reduced masses (AMU), force constants (mDyn/A)
1 2 3
Irreps A" A' A'
Frequencies 385.8687 414.4702 519.9076
Reduced masses 24.3196 21.5030 19.4352
Force constants 2.1335 2.1764 3.0952
备注
(1)程序不能保证在所有情况下都能消除所有多余的虚频,即便程序正常结束,虚频的数目也仍然可能是错误的。所以即便加了 rmimag 关键字,优化结束后用户仍然需要检查虚频数目。如果虚频数目仍然不等于预期值(也就是对于极小值点优化,仍然有虚频;或者对于过渡态优化,没有虚频或者虚频数目大于1个),则需要按 虚频问题 小节的方法手动处理。
(2)如果分子具有点群对称性,但计算时没有指定 nosymm ,则可能无法完全消除所有的虚频,甚至可能导致结构优化不收敛。例如在以上算例中,如果不指定 nosymm ,即令计算在分子的实际点群( \(\rm D_{3h}\) )下进行,则因为不管如何消除两个虚频都会破坏 \(\rm D_{3h}\) 对称性,使得无法消除虚频,进而导致优化不收敛。
(3)限制性优化(不管限制的是笛卡尔坐标还是内坐标)得到的结构,有可能(但不一定)存在无法消掉的虚频。此时如果虚频的数目大于预期值,未必说明当前结构不可用。用户应通过观察虚频的振动模式,自行判断虚频是否是优化时施加的限制条件所导致的,进而判断是否应当消除这些虚频。
锥形交叉点(CI)和最低能量交叉点(MECP)的优化
优化CI和MECP需要调用DL-FIND外部库 [78] ,为此需要在BDFOPT模块的输入里添加以下关键词
solver
0
相应地,前述各算例的 solver 1 代表使用BDF自带的结构优化代码而非DL-FIND来进行优化。原则上,极小值点和过渡态的优化也可用DL-FIND来实现,但效率一般不如BDF自带代码好,因此仅对于CI、MECP优化等BDF自带代码不支持的任务,才应调用DL-FIND。
以下为CI优化的示例输入,该输入文件计算了乙烯的T1态和T2态的锥形交叉点:
#----------------------------------------------------------------------
# Gradient projection method for CI between T1 and T2 by TDDFT BHHLYP/6-31G
#
$COMPASS
Title
C2H4 Molecule test run
Basis
6-31G
Geometry
C 0.00107880 -0.00318153 1.43425054
C 0.00066030 0.00195132 -1.43437339
H 0.05960990 -0.89114967 0.84012371
H -0.05830329 0.95445870 0.96064844
H 0.05950228 0.89180839 -0.84311032
H -0.06267534 -0.95390169 -0.95768311
END geometry
nosymm
$END
$bdfopt
imulti #优化CI
2
maxcycle #最大优化步数
50
tolgrad #均方根梯度的收敛标准
1.d-4
tolstep #均方根步长的收敛标准
5.d-3
$end
$xuanyuan
$end
$SCF
RKS
charge
0
spinmulti
1
atomorb
DFT
BHHLYP
$END
$tddft
imethod
1
isf
1
itda
1
nroot
5
idiag
1
istore
1
crit_e
1.d-8
crit_vec
1.d-6
lefteig
ialda
4
$end
$resp
geom
norder
1
method
2
iroot
1
nfiles
1
$end
$resp
geom
norder
1
method
2
iroot
2
nfiles
1
$end
$resp
iprt
1
QUAD
FNAC
double
norder
1
method
2
nfiles
1
pairs
1
1 1 1 1 1 2
$end
注意该任务不仅需要计算T1态和T2态的梯度,还需要计算T1态和T2态之间的非绝热耦合矢量(由最后一个RESP模块完成),相关关键词参见 tddft ,此处不再赘述。在BDFOPT模块的输入中, imulti 2 代表优化CI。和普通结构优化任务类似,CI优化会输出每步的梯度和步长收敛情况,与此同时还会输出能量收敛情况。例如以上算例最后一步优化的输出为:
Testing convergence in cycle 6
Energy 0.0000E+00 Target: 1.0000E-06 converged? yes
Max step 9.0855E-04 Target: 5.0000E-03 converged? yes component 4
RMS step 5.6602E-04 Target: 3.3333E-03 converged? yes
Max grad 5.5511E-05 Target: 1.0000E-04 converged? yes component 1
RMS grad 2.7645E-05 Target: 6.6667E-05 converged? yes
Converged!
converged
与前述各类优化任务类似,收敛的CI结构保存于 .optgeom 文件内,坐标单位为Bohr。注意能量一行的值总是显示为0,这并不代表CI优化时体系能量不变,而是因为优化CI不会用到能量的收敛情况来判断是否收敛。出于同样的原因, tolene 关键词对于CI优化(以及下述的MECP优化)是没有作用的。
以下是优化MECP的示例输入文件:
#----------------------------------------------------------------------
# Gradient projection method for MECP between S0 and T1 by BHHLYP/6-31G
#
$COMPASS
Title
C2H4 Molecule test run
Basis
6-31G
Geometry
C -0.00000141 0.00000353 0.72393424
C 0.00000417 -0.00000109 -0.72393515
H 0.73780975 -0.54421247 1.29907106
H -0.73778145 0.54421417 1.29907329
H 0.73777374 0.54421576 -1.29907129
H -0.73779427 -0.54423609 -1.29906321
END geometry
nosymm
$END
$bdfopt
imulti
2
maxcycle
50
tolgrad
1.d-4
tolstep
5.d-3
noncouple
$end
$xuanyuan
$end
$SCF
RKS
charge
0
spinmulti
1
atomorb
DFT
BHHLYP
$END
$resp
geom
norder
1
method
1
$end
$SCF
UKS
charge
0
spinmulti
3
atomorb
DFT
BHHLYP
$END
$resp
geom
norder
1
method
1
$end
其中 imulti 2 和 noncouple 关键词指定进行MECP优化。注意MECP优化任务仅需计算两个态(此处为S0态和T1态)的梯度,而无需计算非绝热耦合矢量。MECP优化任务的输出与CI优化任务类似,此处不再赘述。
几何优化常见问题
虚频问题
几何结构优化不仅要求结构收敛(即梯度和步长满足收敛限要求),同时还要求所得结构的虚频数目符合预期值,即当优化极小值点结构时,虚频数目为0;优化过渡态时,虚频数目为1;若虚频数目大于1为高阶鞍点。当实际计算得到的虚频数目与预期值不符时,需要调整结构并重新优化。一般情况下,利用 rmimag关键字 可以解决大部分的虚频数目过多的问题,以及一小部分虚频数目过少的问题。当 rmimag 关键字无法奏效时,用户应当按以下方法手动解决虚频数目不符合预期的问题:
当实际计算得到的虚频数目小于预期值,也即优化过渡态得到虚频数量为0的结构时:此时一般说明得到的过渡态结构定性错误,需要根据化学常识重新准备初猜结构。
当实际计算得到的虚频数目大于预期值时,此时存在两种可能情况:(1)虚频是因为计算的数值误差所导致的,并非真实存在。此时可以通过加大格点、减小积分截断阈值、减小各类收敛阈值(如SCF收敛阈值、结构优化收敛阈值等)等方法解决。(2)体系确实存在虚频。此时应当从输出文件查看虚频对应的简正模,并沿着该简正模方向对收敛的结构进行扰动,然后以扰动后的结构为初猜结构,重新进行优化。
注意无法仅从频率计算结果判断某个虚频是否是数值误差导致的,但一般而言,虚频的绝对值越小,就越可能是数值误差导致的,反之则越可能是真实存在的。
限制性优化(不管限制的是笛卡尔坐标还是内坐标)得到的结构,有可能(但不一定)存在无法消掉的虚频。此时如果虚频的数目大于预期值,未必说明当前结构不可用。用户应通过观察虚频的振动模式,自行判断虚频是否是优化时施加的限制条件所导致的,进而判断是否应当消除这些虚频。
对称性问题
当初始结构具有 \(\rm C_1\) 群以上的点群对称性时,结构优化有可能会破坏点群对称性,例如优化氨分子,初始结构对称性为 \(\rm D_{3h}\) 的平面结构时,结构优化可能会得到对称性为 \(\rm C_{3v}\) 的锥形结构。 默认情况下BDF会强制保持分子点群对称性,除非体系存在一阶Jahn-Teller效应。如果用户希望BDF破坏分子的对称性,可以采取以下方法之一:
仍然在高对称性下优化至收敛,然后计算频率。若存在虚频,按照上一小节方法扰动分子结构来消除虚频。如果分子可以通过破坏对称性来进一步降低能量,那么此时应该发现扰动后的分子结构的对称性已有所降低,继续以该结构为初始结构进行优化即可。
在COMPASS模块中指定采用分子点群的某一个子群,此时程序只会保持该子群对称性不被破坏。若指定的是 \(\rm C_1\) 群,则程序允许以任何方式破坏分子对称性,可以最大程度上提高得到低能量结构的概率,但代价为无法利用点群对称性加速计算,导致计算量增加。
几何优化不收敛
导致几何优化不收敛的因素有很多,包括:
能量、梯度存在数值噪声;
势能面过于平缓;
分子有不止一个稳定波函数,结构优化时波函数在各个稳定解之间来回跳跃,不能稳定地始终收敛到同一个解;
分子结构不合理,如坐标单位错误(如坐标的单位本来是Bohr,但输入文件里指定的单位是Angstrom,或反之),多画或漏画原子,非成键原子之间的距离太近,等等。
某些反应不存在过渡态(要么正反应的活化能为0,要么逆反应的活化能为0),用户如果误以为存在过渡态,进行过渡态优化,则优化不收敛或总是收敛到错误的结构。因此,当过渡态优化始终不收敛时,用户应当考虑当前反应本来就不存在过渡态的可能性,例如做一个柔性扫描,看扫描曲线是否单调变化,如果在整个反应过程中扫描曲线均为单调、平滑变化,则可以认为不存在过渡态(前提是扫描的键长/键角/二面角范围足够大,且扫描步长足够小)。
某些激发态结构优化可能会优化到锥形交叉点附近。例如优化S1结构,有时会优化到S0/S1锥形交叉点附近,此时因为锥形交叉点是附近唯一的局部极小值点,但是势能面在该处不可导,无法满足梯度为0的条件,因此结构优化会在锥形交叉点附近无限振荡。此时用户应重新评估优化S1平衡结构的目的,例如如果是为了计算荧光发射,且从S1势能面上的Franck-Condon点可以直接优化到S0/S1锥形交叉点,则可以较为确定地认为该体系的S1态不发荧光,因为S1态极易从S0/S1锥形交叉点发生内转换弛豫到S0态。必要时,用户可改用 锥形交叉点的优化算法 来优化得到S0/S1锥形交叉点,而不受该点处势能面不可导的影响。
某些TDDFT结构优化可能会优化到势能面上基态波函数不稳定的区域(例如某根键显著拉长,产生双自由基性质),此时程序会因TDDFT出现虚激发能(极个别时候为复激发能),而在RESP模块报错退出。此时用户应根据自己的计算目的,试图收敛得到稳定波函数后再进行计算,或改用TDA,或计算某个更高的激发态。注意这几种方法的结果是不等价的,用户应明确自己的计算目的后再做选择,不可仅因其中一种方法解决了虚激发能的问题,就盲目相信其结果。
极个别情况下,因为程序构建的内坐标含有接近180度的键角,导致优化失败。如前所述,一般来说程序会反复尝试重新构建内坐标,直至尝试10次仍未收敛才报错退出,所以BDF因内坐标问题报错退出的概率应较其他很多量化程序低。
如遇到几何优化不收敛,或虽然尚未达到最大收敛次数但毫无收敛趋势的情形,经反复检查分子三维结构无误且合理(所谓结构合理,既包括用户提供的初始结构无误,例如没有漏画、多画、错画原子等,也包括优化后的结构合理,没有不符合化学常识的结构拥挤、扭曲等情况)、波函数收敛正常以后,可依次尝试以下各方法解决:
以优化不收敛的任务的最后一帧结构为初始结构,重新开始优化。除了手动将最后一帧的结构坐标复制到输入文件里以外,一个更简单的办法是在COMPASS模块里加入
restart关键词,如:
$compass
title
CH3Cl geomopt
basis
def2-SV(P)
geometry
C 2.67184328 0.03549756 -3.40353093
H 2.05038141 -0.21545378 -2.56943947
H 2.80438882 1.09651909 -3.44309081
H 3.62454948 -0.43911916 -3.29403269
Cl 1.90897396 -0.51627638 -4.89053325
end geometry
restart
$end
假设输入文件的文件名为 CH3Cl-opt.inp ,则此时程序自动读取 CH3Cl-opt.optgeom 里的坐标作为初始结构(注意此时程序虽然不会用到 geometry 字段里的分子坐标,但该分子坐标不能删去)。乍看起来,这样做似乎与简单地增加几何优化最大迭代步数无异,但实际上这样做的效果往往比单纯增加最大迭代步数更好,例如优化100步后重新读取结构再优化50步,收敛概率常常比连续迭代150步更高,这是因为重新读取结构继续优化时,程序重新产生了初始Hessian,进而避免了准牛顿法连续多步近似构建Hessian所累积的误差。
减小优化步长,或称置信半径(trust radius)。方法为使用trust关键词,如
$bdfopt
solver
1
trust
0.05
$end
默认的置信半径为0.3,因此新设置的置信半径应当小于0.3。注意程序如果检测到置信半径太小,会动态地增加置信半径,为了避免这一行为,可以将置信半径设为负值,如
$bdfopt
solver
1
trust
-0.05
$end
即表示,初始置信半径设为0.05,且在整个结构优化过程中禁止置信半径超过0.05。
对于过渡态优化,可用
recalchess关键词指定每隔若干步重新计算精确Hessian。如
$bdfopt
solver
1
iopt
10
hess
init
recalchess
10
$end
表示除在结构优化之前计算精确Hessian外,每隔10步结构优化重新计算一次精确Hessian。
加大格点,减小积分截断阈值及SCF等的收敛阈值,以减小数值误差。注意该方法只在结构优化几乎收敛但无法完全收敛时有用。
改用DL-Find优化器,在直角坐标下优化结构:
$bdfopt
solver
0
$end
其中 solver 0 表示使用DL-Find优化器而非BDF自带的优化器。因DL-Find默认在直角坐标下优化结构,所以无需用额外的关键词指定在直角坐标下优化。该方法适用于程序因内坐标键角接近180度,经多次重启优化器仍无法解决进而报错的情形(此时应跳过以上各解决方法,直接尝试本方法,因为这种情况下本方法解决问题的概率最大,如不能解决问题再依次尝试以上各方法),也适用于虽然程序报错不是因为键角接近180度问题,但所计算体系不太适合用内坐标描述,因而优化不收敛的情形(例如体系是较大的非共价团簇)。
在应用以上方法之前,用户应检查当前这个不收敛的计算所得结构相比用户提供的初猜结构哪个更合理,用其中较为合理的那个结构作为接下来重新优化的初猜结构。如果不仅结构优化后的结构不合理,还发现初猜结构也不合理,则应重新准备初猜结构。这对于过渡态优化尤其重要,如果第一次结构优化时分子结构被优化到过渡态区域以外,则之后无论尝试什么方法也很难将结构重新优化回过渡态区域附近。因此,不经检查结构是否合理、盲目地以前一次结构优化的最后一帧结构(或前一次结构优化的初猜结构)作为下一次优化的初猜结构,是不可取的。
溶剂化模型
溶剂化模型用于计算溶质和溶剂之间的相互作用,一般分为隐式溶剂模型(连续介质模型)和显式溶剂模型两种。 在BDF中,对于连续溶剂模型,可以选择IEFPCM、SS(V)PE、CPCM、COSMO、 ddCOSMO(domain-decomposition COSMO solvation model)以及SMD,对于显示溶剂模型采用QM/MM方法,结合pDymamo2.0程序包进行计算。
BDF溶剂化模型支持的功能:
PCMs |
Ground state |
Excited state |
|||
|---|---|---|---|---|---|
Single-point |
Gradient |
Hessian |
Single-point |
Gradient |
|
COSMO |
√ |
√ |
√ |
√ |
√ |
CPCM |
√ |
√ |
√ |
√ |
√ |
SS(V)PE |
√ |
√ |
√ |
√ |
√ |
IEFPCM |
√ |
√ |
√ |
√ |
√ |
SMD |
√ |
√ |
√ |
√ |
√ |
溶剂类型设置
在 SCF 模块中加入 solvent 关键词,表示要进行溶剂化效应计算,紧跟一行可以输入溶剂类型,比如 water 。
以甲醛分子在水溶液中的计算为例,其输入文件为:
$COMPASS
Title
ch2o Molecule test run
Basis
6-31g
Geometry
C 0.00000000 0.00000000 -0.54200000
O 0.00000000 0.00000000 0.67700000
H 0.00000000 0.93500000 -1.08200000
H 0.00000000 -0.93500000 -1.08200000
END geometry
nosymm
unit
ang
$END
$xuanyuan
$END
$SCF
rks
dft
b3lyp
solvent #溶剂化计算开关
water #指定溶剂
grid
medium
$END
溶剂类型的指定可以输入 BDF支持的溶剂类型列表 中的名称或者别名。对于表中没有的溶剂,可以输入介电常数。格式如下:
solvent
user #用户指定
dielectric
78.3553 #输入介电常数
溶剂模型设置
连续介质模型是将溶剂视为有一定介电常数的可极化的连续介质。
目前BDF支持的溶剂模型有ddCOSMO、COSMO、CPCM、IEFPCM、SS(V)PE以及SMD, 对应的关键词为 ddcosmo 、 cosmo、 cpcm、 iefpcm、 ssvpe、 smd。输入为:
solvent
water
solmodel
IEFPCM #溶剂模型
对于COSMO和CPCM,可以通过 cosmoFactorK 来指定the dielectric screening factor, \(f_\epsilon=\frac{\epsilon-1}{\epsilon+k}\) ,中k的大小。对于COSMO,k默认为0.5;对于CPCM,k默认为0。
cosmoFactorK
0.5
对于SMD模型,可以手动指定溶剂的折射率、Abraham氢键酸度、Abraham氢键碱度、表面张力、芳香度、卤素度
refractiveIndex # 折射率
1.43
HBondAcidity # Abraham氢键酸度
0.229
HBondBasicity # Abraham氢键碱度
0.265
SurfaceTensionAtInterface # 表面张力
61.24
CarbonAromaticity # 芳香度
0.12
ElectronegativeHalogenicity # 卤素度
0.24
备注
使用SMD模型将关闭 溶剂化自由能非静电部分 的计算,取而代之将计算SMx系列的 \(\Delta G_{CDS}\)
孔穴自定义设置
连续介质模型将视为连续介质的溶剂根据溶质分子来形成孔穴,孔穴的形状会对溶剂化能的计算产生较大的影响。对于连续介质模型,有多种孔穴的定义:vdW(van der Waals surface), SES(solvent-excluded surface), SAS(solvent-accessible surface)等。
在BDF中默认采用1.1倍的UFF半径来构建vdW表面的孔穴。
对于COSMO、CPCM、IEFPCM、SS(V)PE以及SMD溶剂模型,可以通过 cavity, RadiusType, vdWScale, radii, uatm, acidHRadius 等关键词来自定义孔穴的形状。
cavity # 生成孔穴表面的方式
swig # swig | switching | ses | sphere,默认为 swig
uatm # 联合原子拓扑方法
false # false | true,默认为 false
radiusType
UFF # UFF | Bondi,默认为 UFF
vdWScale
1.1 # 默认 1.1, 即 1.1 倍 RadiusType 半径
radii
1=1.4430 2=1.7500 # 第一个原子的半径设为 1.4430Å, 第二个原子的半径设为 1.7500Å
# 等号间不能有空格, 一行最多128字符, 一行写不下可以加上radii之后新增一行
# radii的设置会覆盖 vdWScale*RadiusType 中相同原子的设置
radii
H=1.4430 O=1.7500 # 同上, 将 H 原子的半径设为1.4430Å, 将 O 原子的半径设为 1.7500Å。两种方式可以混合使用。
acidHRadius # 单独设置酸性H半径,单位 Å
1.2
通过 cavity 关键词,可以控制生成孔穴表面的方式
switching表示用平滑函数来处理vdW表面的格点权重swig表示 switching/gaussian,即在switching的基础上再使用高斯函数对格点处的点电荷做平滑处理sphere表示形成一个圆球状的孔穴来包裹整个分子。
uatm 表示将H原子联合进重原子共同形成孔穴。
另外还可以通过 cavityNGrid 或 cavityPrecision 来指定孔穴的格点精度(每个原子表面的最大tesserae数)。
cavityNGrid # 控制每个原子生成的孔穴表面的格点数, 会自动调整至最近的 lebedev 格点
302 # 默认为 302
# 或者
cavityPrecision
medium # ultraCoarse | coarse | medium | fine | ultraFine,默认为 medium
基态溶剂化能计算
对于基态溶剂化能计算,通常只需要在 SCF 模块中设定溶剂类型以及溶剂化模型,其余参数使用默认即可。
以甲醛分子在水溶液中使用SMD模型的计算为例,其输入文件为:
$COMPASS
Title
ch2o Molecule test run
Basis
6-31g
Geometry
C 0.00000000 0.00000000 -0.54200000
O 0.00000000 0.00000000 0.67700000
H 0.00000000 0.93500000 -1.08200000
H 0.00000000 -0.93500000 -1.08200000
END geometry
$END
$xuanyuan
$END
$SCF
rks
dft
gb3lyp
solvent #溶剂化计算开关
water #指定溶剂
solmodel #指定溶剂化模型
smd
$END
备注
使用 cosmosave 关键词可以保存孔穴体积、表面积,tesserae坐标、电荷、面积等信息到工作目录的.cosmo文件,如有需要,可以利用 $BDFHOME/sbin/conv2gaucosmo.py 可以将其转化为类似gaussian的cosmors关键词所生成的文件的格式。
非静电溶剂化能计算
溶剂化自由能包括静电溶剂化能以及非静电溶剂化能。上述的PCM模型计算了静电溶剂化能。非静电溶剂化能一般可以分为为孔穴能 \(\Delta G_{cav}\) 和色散-排斥能 \(\Delta G_{dis-rep}\) 。 孔穴能是在假设溶质溶剂之间无相互作用时,将溶质分子从气相移入液相形成孔穴所做的功。可以用基于定标粒子理论(SPT)的Pierotti-Claverie公式来进行计算。色散能与排斥能可以用粒子对势近似法来计算。
在BDF中,默认不开启非静电溶剂化能的计算,可以通过以下关键词来开启非静电溶剂化能的计算
nonels
dis rep cav # 色散能 排斥能 孔穴能
solventAtoms # 溶剂分子的各类型原子的个数(分子式)
H2O1 # 默认为H2O1,不能省略1,因为不区分大小写后无法确定元素符号是几个字母
solventRho # 溶剂分子数密度,单位 molecules Å^-3
0.03333
solventRadius # 溶剂分子半径,单位 Å
1.385
备注
指定cav时,除非solvent指定为water会自动使用默认值,其他溶剂必须手动指定 solventRho、 solventRadius。
指定rep或dis时,除非solvent指定为water会自动使用默认值,其他溶剂必须手动指定 solventRho、 solventAtoms。
一些常见溶剂的分子半径
Solvent |
Water |
Tetrahydrofuran |
Cyclohexane |
Methanol |
Ethanol |
Tetrachloromethane |
Radius(Å) |
1.385 |
2.900 |
2.815 |
1.855 |
2.180 |
2.685 |
计算色散排斥能以及孔穴能时,默认使用的Bondi半径,也可以自定义计算色散排斥能或者孔穴能时的半径。
通过 solventAtomicSASRadii 关键词来指定计算色散排斥能时所构建的SAS孔穴的溶剂分子中每类原子的半径。
通过 radiiForCavEnergy 关键词来指定计算孔穴能时的半径,并且可以通过 acidHRadiusForCavEnergy 关键词来单独设置酸性H的半径。
solventAtomicSASRadii # 计算色散排斥能时,构建SAS孔穴的溶剂分子中每类原子的半径
H=1.20 O=1.50
radiiForCavEnergy # 计算孔穴能的溶质半径
H=1.4430 O=1.7500 # 注意事项同radii
acidHRadiusForCavEnergy # 计算孔穴能的溶质半径,单独设置酸性H,单位 Å
1.2
非平衡溶剂化新理论简介
激发态溶剂化效应需要考虑非平衡溶剂化现象。溶剂的极化可以分为快极化和慢极化部分。垂直吸收和发射过程十分迅速,溶剂的偶极和构型不能迅速调整至与溶质电荷达到平衡的状态,于是需要考虑非平衡溶剂化效应。
传统非平衡溶剂化理论中平衡态到非平衡态的可逆功积分方式存在与热力学第二定律相矛盾的问题,会导致溶剂重组能的高估。在进行态特定计算时,采用了李象远教授课题组发展的非平衡溶剂化新理论(X. Y. Li. Int. J. Quantum Chem. 2015, 115(11): 700-721)。
激发态溶剂化效应计算
激发态溶剂化效应在隐式模型中有 线性响应 (linear-response, LR)和 态特定 (state-specific, SS)的处理方式。
垂直吸收计算
以下是采用 线性响应 计算甲醛分子激发态非平衡溶剂化效应的输入文件:
$COMPASS
Title
ch2o Molecule test run
Basis
6-31g
Geometry
C 0.00000000 0.00000000 -0.54200000
O 0.00000000 0.00000000 0.67700000
H 0.00000000 0.93500000 -1.08200000
H 0.00000000 -0.9350000 -1.08200000
END geometry
nosymm
unit
ang
$END
$xuanyuan
$END
$SCF
rks
dft
b3lyp
grid
medium
solvent
user # 用户指定
dielectric
78.3553 # 输入介电常数
opticalDielectric
1.7778 # 光介电常数
solmodel
iefpcm
$END
$TDDFT
iroot
8
solneqlr
$END
其中,在 TDDFT 中加入 solneqlr 关键词,表示要进行非平衡溶剂化效应计算。
备注
计算非平衡溶剂化效应时,溶剂如果为用户指定的(详见 BDF支持的溶剂类型列表 ),需要设置光介电常数,关键词为 opticalDielectric。
BDF目前支持一阶微扰态特定的能量计算(ptSS),以下是采用 态特定 计算丙烯醛分子激发态非平衡溶剂化效应的输入文件:
$COMPASS
Title
SS-PCM of S-trans-acrolein Molecule
Basis
cc-PVDZ
Geometry
C 0.55794100 -0.45384200 -0.00001300
H 0.44564200 -1.53846100 -0.00002900
C -0.66970500 0.34745600 -0.00001300
H -0.50375600 1.44863100 -0.00005100
C 1.75266800 0.14414300 0.00001100
H 2.68187400 -0.42304000 0.00001600
H 1.83151500 1.23273300 0.00002700
O -1.78758800 -0.11830000 0.00001600
END geometry
$END
$xuanyuan
$END
$SCF
rks
dft
PBE0
solvent
water
solmodel
iefpcm
$END
$TDDFT
iroot
5
istore
1
$END
$resp
nfiles
1
method
2
iroot
1 2 3
norder
0
solneqss
$end
其中,在 resp 中加入 solneqss 关键词,表示要进行态特定非平衡溶剂化效应计算。指定 norder 为 0 ,表示不进行梯度的计算。用 iroot 指定计算哪些态。
在文件中的输出:
-Energy correction based on constrant equilibrium theory with relaxed density
*State 1 -> 0
Corrected vertical absorption energy = 3.6935 eV
Nonequilibrium solvation free energy = -0.0700 eV
Equilibrium solvation free energy = -0.1744 eV
其中 Corrected vertical absorption energy 表示采用李象远教授课题组发展的非平衡溶剂化新理论计算的激发能矫正。
上面的例子中,垂直吸收能为 \(3.69eV\)。
BDF目前还支持矫正的线性响应的计算(corrected linear response, cLR),以下是采用cLR计算丙烯醛分子激发态非平衡溶剂化效应的输入文件:
$COMPASS
Title
cLR-PCM of S-trans-acrolein Molecule
Basis
cc-PVDZ
Geometry
C 0.55794100 -0.45384200 -0.00001300
H 0.44564200 -1.53846100 -0.00002900
C -0.66970500 0.34745600 -0.00001300
H -0.50375600 1.44863100 -0.00005100
C 1.75266800 0.14414300 0.00001100
H 2.68187400 -0.42304000 0.00001600
H 1.83151500 1.23273300 0.00002700
O -1.78758800 -0.11830000 0.00001600
END geometry
$END
$xuanyuan
$END
$SCF
rks
dft
PBE0
solvent
water
solmodel
iefpcm
$END
$TDDFT
iroot
5
istore
1
$END
$TDDFT
iroot
5
istore
1
solneqlr
$END
$resp
nfiles
1
method
2
iroot
1
norder
0
solneqlr
solneqss
$end
在文件中的找到 第一个TDDFT 的输出, 以及resp模块中的cLR输出:
No. 1 w= 3.7475 eV -191.566549 a.u. f= 0.0001 D<Pab>= 0.0000 Ova= 0.4683
CV(0): A( 15 )-> A( 16 ) c_i: 0.9871 Per: 97.4% IPA: 5.808 eV Oai: 0.4688
CV(0): A( 15 )-> A( 17 ) c_i: 0.1496 Per: 2.2% IPA: 9.144 eV Oai: 0.4392
...
Excitation energy correction(cLR) = -0.0377 eV
可算得cLR的激发能为 \(3.7475-0.0377=3.7098eV\)。
激发态几何优化
对于几何优化过程,溶剂有足够的时间进行响应,应考虑平衡溶剂效应。
需要在 tddft 以及 resp 模块中加入 soleqlr 关键词来表示平衡溶剂效应的计算。输入文件的其他部分以及输出,与 TDDFT相关章节 类似,此处不再赘述。
以下是苯酚分子的激发态溶剂化效应的几何优化计算
$COMPASS
Geometry
C -1.15617700 -1.20786100 0.00501300
C -1.85718200 0.00000000 0.01667700
C -1.15617700 1.20786100 0.00501300
C 0.23962700 1.21165300 -0.01258600
C 0.93461900 0.00000000 -0.01633400
C 0.23962700 -1.21165300 -0.01258600
H -1.69626800 -2.15127300 0.00745900
H -2.94368500 0.00000000 0.02907200
H -1.69626800 2.15127300 0.00745900
H 0.80143900 2.14104700 -0.03186000
H 0.80143900 -2.14104700 -0.03186000
O 2.32295900 0.00000000 -0.08796400
H 2.68364400 0.00000000 0.81225800
End geometry
basis
6-31G
$END
$bdfopt
solver
1
$end
$XUANYUAN
$END
$SCF
DFT
gb3lyp
rks
solModel
iefpcm
solvent
water
$END
$TDDFT
iroot
5
istore
1
soleqlr
$END
$resp
geom
soleqlr
method
2
nfiles
1
iroot
1
$end
垂直发射计算
在激发态的平衡几何结构下,进行ptSS或者cLR的平衡溶剂化效应的计算,将保存对应的溶剂慢极化电荷。在随后的scf模块中加入 emit 关键词,来计算非平衡的基态能量。以丙烯醛分子为例,采用ptSS计算激发态,对应的输入文件如下:
$COMPASS
Geometry
C -1.810472 0.158959 0.000002
H -1.949516 1.241815 0.000018
H -2.698562 -0.472615 -0.000042
C -0.549925 -0.413873 0.000029
H -0.443723 -1.502963 -0.000000
C 0.644085 0.314498 0.000060
H 0.618815 1.429158 -0.000047
O 1.862127 -0.113145 -0.000086
End geometry
basis
cc-PVDZ
$END
$XUANYUAN
$END
$SCF
DFT
PBE0
rks
solModel
iefpcm
solvent
water
$END
$TDDFT
iroot
5
istore
1
#soleqlr
$END
$resp
nfiles
1
method
2
iroot
1
norder
0
#soleqlr
soleqss
$end
$SCF
DFT
PBE0
rks
solModel
iefpcm
solvent
water
emit
$END
需要注意指定 soleqss 来计算平衡溶剂化效应。在文件中的输出为:
-Energy correction based on constrant equilibrium theory
*State 1 -> 0
Corrected vertical emission energy = 2.8118 eV
Nonequilibrium solvation free energy = -0.0964 eV
Equilibrium solvation free energy = -0.1145 eV
其中 Corrected vertical emission energy 表示采用李象远教授课题组发展的非平衡溶剂化新理论计算的激发能矫正。
上面的例子中,垂直发射能为 \(2.81eV\)。
采用cLR计算时,需要在文件中的找到 第一个TDDFT 的输出, 以及resp模块中的cLR输出,并与两个scf的 E_tot 之差进行相加,得到最终的垂直发射能。
采用显式溶剂和隐式溶剂相结合的方法计算激发态溶剂化效应
激发态溶剂化效应可以采用显式溶剂和隐式溶剂相结合的方法计算。以水溶液为例,由于溶质分子的HOMO和LUMO轨道有可能弥散到 第一水合层,所以在进行激发态计算时可以将第一水合层的水分子包括在TDDFT计算区域,而其余部分用隐式溶剂处理。
以芥子酸(sinapic acid)为例。为了确定溶质分子的第一水合层,可以采用Amber程序将芥子酸分子置于小的水盒子中进行分子动力学模拟。 待体系平衡后,可分析溶质分子周围水分子分布情况,从而确定第一水合层。当然,也可以选取多帧结构进行计算,然后取平均。
水合层分子选取可以采用VMD程序完成。假设输入为pdb文件,在命令行中可以选择第一水合层分子,并保存为pdb文件。命令如下:
atomselect top "same resid as (within 3.5 of not water)" # 选择第一水合层
atomselect0 writepdb sa.pdb #溶质分子和第一水合层保存于pdb文件
上例中选取了与溶质分子相距3.5埃范围内的所有水分子,并且水分子的三个原子中只要有一个在截断范围内,就选择整个分子。选取结果如图所示:

依据sa.pdb文件中的坐标信息,进行TDDFT计算,输入文件如下:
$COMPASS
Title
SA Molecule test run
Basis
6-31g
Geometry
C 14.983 14.539 6.274
C 14.515 14.183 7.629
C 13.251 14.233 8.118
C 12.774 13.868 9.480
C 11.429 14.087 9.838
C 10.961 13.725 11.118
O 9.666 13.973 11.525
C 8.553 14.050 10.621
C 11.836 13.125 12.041
O 11.364 12.722 13.262
C 13.184 12.919 11.700
O 14.021 12.342 12.636
C 15.284 11.744 12.293
C 13.648 13.297 10.427
O 14.270 14.853 5.341
O 16.307 14.468 6.130
H 15.310 13.847 8.286
H 12.474 14.613 7.454
H 10.754 14.550 9.127
H 7.627 14.202 11.188
H 8.673 14.888 9.924
H 8.457 13.118 10.054
H 10.366 12.712 13.206
H 15.725 11.272 13.177
H 15.144 10.973 11.525
H 15.985 12.500 11.922
H 14.687 13.129 10.174
H 16.438 14.756 5.181
O 18.736 9.803 12.472
H 18.779 10.597 11.888
H 19.417 10.074 13.139
O 18.022 14.021 8.274
H 17.547 14.250 7.452
H 18.614 13.310 7.941
O 8.888 16.439 7.042
H 9.682 16.973 6.797
H 8.217 17.162 7.048
O 4.019 14.176 11.140
H 4.032 13.572 10.360
H 4.752 14.783 10.885
O 16.970 8.986 14.331
H 17.578 9.273 13.606
H 17.497 8.225 14.676
O 8.133 17.541 10.454
H 8.419 17.716 11.386
H 8.936 17.880 9.990
O 8.639 12.198 13.660
H 7.777 11.857 13.323
H 8.413 13.155 13.731
O 13.766 11.972 4.742
H 13.858 12.934 4.618
H 13.712 11.679 3.799
O 10.264 16.103 14.305
H 9.444 15.605 14.054
H 10.527 15.554 15.084
O 13.269 16.802 3.701
H 13.513 16.077 4.325
H 14.141 17.264 3.657
O 13.286 14.138 14.908
H 13.185 14.974 14.393
H 13.003 13.492 14.228
O 16.694 11.449 15.608
H 15.780 11.262 15.969
H 16.838 10.579 15.161
O 7.858 14.828 14.050
H 7.208 15.473 13.691
H 7.322 14.462 14.795
O 15.961 17.544 3.706
H 16.342 16.631 3.627
H 16.502 17.866 4.462
O 10.940 14.245 16.302
H 10.828 13.277 16.477
H 11.870 14.226 15.967
O 12.686 10.250 14.079
H 11.731 10.151 14.318
H 12.629 11.070 13.541
O 9.429 11.239 8.483
H 8.927 10.817 7.750
H 9.237 12.182 8.295
O 17.151 15.141 3.699
H 17.124 14.305 3.168
H 18.133 15.245 3.766
O 17.065 10.633 9.634
H 16.918 10.557 8.674
H 17.024 9.698 9.909
O 17.536 14.457 10.874
H 18.014 13.627 11.089
H 17.683 14.460 9.890
O 5.836 16.609 13.299
H 4.877 16.500 13.549
H 5.760 16.376 12.342
O 19.014 12.008 10.822
H 18.249 11.634 10.308
H 19.749 11.655 10.256
O 15.861 14.137 15.750
H 14.900 13.990 15.574
H 16.185 13.214 15.645
O 11.084 9.639 10.009
H 11.641 9.480 9.213
H 10.452 10.296 9.627
O 14.234 10.787 16.235
H 13.668 10.623 15.444
H 13.663 10.376 16.925
O 14.488 8.506 13.105
H 13.870 9.136 13.550
H 15.301 8.683 13.628
O 14.899 17.658 9.746
H 15.674 18.005 9.236
H 15.210 16.754 9.926
O 8.725 13.791 7.422
H 9.237 13.488 6.631
H 8.845 14.770 7.309
O 10.084 10.156 14.803
H 9.498 10.821 14.366
H 10.215 10.613 15.669
O 5.806 16.161 10.582
H 5.389 16.831 9.993
H 6.747 16.470 10.509
O 6.028 13.931 7.206
H 5.971 14.900 7.257
H 6.999 13.804 7.336
O 17.072 12.787 2.438
H 16.281 12.594 1.885
H 17.062 11.978 3.013
END geometry
nosymm
mpec+cosx
$END
$xuanyuan
$end
$SCF
rks
dft
b3lyp
solvent
water
grid
medium
$END
# input for tddft
$tddft
iroot # Calculate 1 root for each irrep. By default, 10 roots are calculated
1 # for each irrep
memjkop # maxium memeory for Coulomb and Exchange operator. 1024 MW (Mega Words)
1024
$end
BDF中支持的溶剂类型列表
Name |
Short Name |
\({\epsilon}\) |
\({\epsilon_{opt}}\) |
|---|---|---|---|
water |
H2O |
78.3553 |
1.7764 |
acetic acid |
ACETACID |
6.2528 |
1.8824 |
acetone |
ACETONE |
20.4930 |
1.8463 |
acetonitrile |
ACETNTRL |
35.6880 |
1.8069 |
acetophenone |
ACETPHEN |
17.4400 |
2.3630 |
aniline |
ANILINE |
6.8882 |
2.5163 |
anisole |
ANISOLE |
4.2247 |
2.3025 |
benzaldehyde |
BENZALDH |
18.2200 |
2.3910 |
benzene |
BENZENE |
2.2706 |
2.2533 |
benzonitrile |
BENZNTRL |
25.5920 |
2.3375 |
benzyl chloride |
BENZYLCL |
6.7175 |
2.3688 |
1-bromo-2-methylpropane |
BRISOBUT |
7.7792 |
2.0587 |
bromobenzene |
BRBENZEN |
5.3954 |
2.4327 |
bromoethane |
BRETHANE |
9.0100 |
2.0275 |
bromoform |
BROMFORM |
4.2488 |
2.5616 |
1-bromooctane |
BROCTANE |
5.0244 |
2.1095 |
1-bromopentane |
BRPENTAN |
6.2690 |
2.0872 |
2-bromopropane |
BRPROPA2 |
9.3610 |
2.0309 |
1-bromopropane |
BRPROPAN |
8.0496 |
2.0572 |
butanal |
BUTANAL |
13.4500 |
1.9163 |
butanoic acid |
BUTACID |
2.9931 |
1.9544 |
1-butanol |
BUTANOL |
17.3320 |
1.9580 |
2-butanol |
BUTANOL2 |
15.9440 |
1.9538 |
butanone |
BUTANONE |
18.2460 |
1.9011 |
butanonitrile |
BUTANTRL |
24.2910 |
1.9160 |
butyl acetate |
BUTILE |
4.9941 |
1.9435 |
butylamine |
NBA |
4.6178 |
1.9687 |
n-butylbenzene |
NBUTBENZ |
2.3600 |
2.2195 |
sec-butylbenzene |
SBUTBENZ |
2.3446 |
2.2186 |
tert-butylbenzene |
TBUTBENZ |
2.3447 |
2.2282 |
carbon disulfide |
CS2 |
2.6105 |
2.6631 |
carbon tetrachloride |
CARBNTET |
2.2280 |
2.1319 |
chlorobenzene |
CLBENZEN |
5.6968 |
2.3229 |
sec-butyl chloride |
SECBUTCL |
8.3930 |
1.9519 |
chloroform |
CHCL3 |
4.7113 |
2.0906 |
1-chlorohexane |
CLHEXANE |
5.9491 |
2.0161 |
1-chloropentane |
CLPENTAN |
6.5022 |
1.9957 |
1-chloropropane |
CLPROPAN |
8.3548 |
1.9263 |
o-chlorotoluene |
OCLTOLUE |
4.6331 |
2.3311 |
m-cresol |
M-CRESOL |
12.4400 |
2.3833 |
o-cresol |
O-CRESOL |
6.7600 |
2.3596 |
cyclohexane |
CYCHEXAN |
2.0165 |
2.0352 |
cyclohexanone |
CYCHEXON |
15.6190 |
2.1045 |
cyclopentane |
CYCPENTN |
1.9608 |
1.9782 |
cyclopentanol |
CYCPNTOL |
16.9890 |
2.1112 |
cyclopentanone |
CYCPNTON |
13.5800 |
2.0638 |
cis-decalin |
DECLNCIS |
2.2139 |
2.1934 |
trans-decalin |
DECLNTRA |
2.1781 |
2.1594 |
decalin (cis/trans mixture) |
DECLNMIX |
2.1960 |
2.1765 |
n-decane |
DECANE |
1.9846 |
1.9887 |
1-decanol |
DECANOL |
7.5305 |
2.0655 |
1,2-dibromoethane |
EDB12 |
4.9313 |
2.3676 |
dibromomethane |
DIBRMETN |
7.2273 |
2.3778 |
dibutyl ether |
BUTYLETH |
3.0473 |
1.9578 |
o-dichlorobenzene |
ODICLBNZ |
9.9949 |
2.4072 |
1,2-dichloroethane |
EDC12 |
10.1250 |
2.0874 |
cis-dichloroethylene |
C12DCE |
9.2000 |
2.0996 |
trans-dichloroethylene |
T12DCE |
2.1400 |
2.0892 |
dichloromethane |
DCM |
8.9300 |
2.0283 |
diethyl ether |
ETHER |
4.2400 |
1.8295 |
diethyl sulfide |
ET2S |
5.7230 |
2.0822 |
diethylamine |
DIETAMIN |
3.5766 |
1.9221 |
diiodomethane |
MI |
5.3200 |
3.0363 |
diisopropyl ether |
DIPE |
3.3800 |
1.8712 |
dimethyl disulfide |
DMDS |
9.6000 |
2.3375 |
dimethyl sulfoxide |
DMSO |
46.8260 |
2.0079 |
n,n-dimethylacetamide |
DMA |
37.7810 |
2.0678 |
cis-1,2-dimethylcyclohexane |
CISDMCHX |
2.0600 |
2.0621 |
n,n-dimethylformamide |
DMF |
37.2190 |
2.0463 |
2,4-dimethylpentane |
DMEPEN24 |
1.8939 |
1.9085 |
2,4-dimethylpyridine |
DMEPYR24 |
9.4176 |
2.2530 |
2,6-dimethylpyridine |
DMEPYR26 |
7.1735 |
2.2359 |
1,4-dioxane |
DIOXANE |
2.2099 |
2.0232 |
diphenyl ether |
PHOPH |
3.7300 |
2.4923 |
dipropylamine |
DPROAMIN |
2.9112 |
1.9740 |
n-dodecane |
DODECAN |
2.0060 |
2.0209 |
1,2-ethanediol |
MEG |
40.2450 |
2.0501 |
ethanethiol |
ETSH |
6.6670 |
2.0478 |
ethanol |
ETHANOL |
24.8520 |
1.8526 |
ethyl acetate |
ETOAC |
5.9867 |
1.8832 |
ethyl formate |
ETOME |
8.3310 |
1.8493 |
ethylbenzene |
EB |
2.4339 |
2.2377 |
ethylphenyl ether |
PHENETOL |
4.1797 |
2.2729 |
fluorobenzene |
C6H5F |
5.4200 |
2.1562 |
1-fluorooctane |
FOCTANE |
3.8900 |
1.9418 |
formamide |
FORMAMID |
108.9400 |
2.0944 |
formic acid |
FORMACID |
51.1000 |
1.8807 |
n-heptane |
HEPTANE |
1.9113 |
1.9260 |
1-heptanol |
HEPTANOL |
11.3210 |
2.0303 |
2-heptanone |
HEPTNON2 |
11.6580 |
1.9847 |
4-heptanone |
HEPTNON4 |
12.2570 |
1.9794 |
n-hexadecane |
HEXADECN |
2.0402 |
2.0578 |
n-hexane |
HEXANE |
1.8819 |
1.8904 |
hexanoic acid |
HEXNACID |
2.6000 |
2.0059 |
1-hexanol |
HEXANOL |
12.5100 |
2.0102 |
2-hexanone |
HEXANON2 |
14.1360 |
1.9620 |
1-hexene |
HEXENE |
2.0717 |
1.9146 |
1-hexyne |
HEXYNE |
2.6150 |
1.9569 |
iodobenzene |
C6H5I |
4.5470 |
2.6244 |
1-iodobutane |
IOBUTANE |
6.1730 |
2.2503 |
iodoethane |
C2H5I |
7.6177 |
2.2901 |
1-iodohexadecane |
IOHEXDEC |
3.5338 |
2.1922 |
iodomethane |
CH3I |
6.8650 |
2.3654 |
1-iodopentane |
IOPENTAN |
5.6973 |
2.2377 |
1-iodopropane |
IOPROPAN |
6.9626 |
2.2674 |
isopropylbenzene |
CUMENE |
2.3712 |
2.2246 |
p-isopropyltoluene |
P-CYMENE |
2.2322 |
2.2228 |
mesitylene |
MESITYLN |
2.2650 |
2.2482 |
methanol |
METHANOL |
32.6130 |
1.7657 |
2-methoxyethanol |
EGME |
17.2000 |
1.9667 |
methyl acetate |
MEACETAT |
6.8615 |
1.8534 |
methyl benzoate |
MEBNZATE |
6.7367 |
2.2995 |
methyl butanoate |
MEBUTATE |
5.5607 |
1.9260 |
methyl formate |
MEFORMAT |
8.8377 |
1.8045 |
4-methyl-2-pentanone |
MIBK |
12.8870 |
1.9494 |
methyl propanoate |
MEPROPYL |
6.0777 |
1.8975 |
2-methyl-1-propanol |
ISOBUTOL |
16.7770 |
1.9474 |
2-methyl-2-propanol |
TERBUTOL |
12.4700 |
1.9260 |
n-methylaniline |
NMEANILN |
5.9600 |
2.4599 |
methylcyclohexane |
MECYCHEX |
2.0240 |
2.0252 |
n-methylformamide (E/Z mixture) |
NMFMIXTR |
181.5600 |
2.0503 |
2-methylpentane |
ISOHEXAN |
1.8900 |
1.8810 |
2-methylpyridine |
MEPYRID2 |
9.9533 |
2.2371 |
3-methylpyridine |
MEPYRID3 |
11.6450 |
2.2620 |
4-methylpyridine |
MEPYRID4 |
11.9570 |
2.2611 |
nitrobenzene |
C6H5NO2 |
34.8090 |
2.4218 |
nitroethane |
C2H5NO2 |
28.2900 |
1.9368 |
nitromethane |
CH3NO2 |
36.5620 |
1.9091 |
1-nitropropane |
NTRPROP1 |
23.7300 |
1.9650 |
2-nitropropane |
NTRPROP2 |
25.6540 |
1.9444 |
o-nitrotoluene |
ONTRTOLU |
25.6690 |
2.3870 |
n-nonane |
NONANE |
1.9605 |
1.9751 |
1-nonanol |
NONANOL |
8.5991 |
2.0543 |
5-nonanone |
NONANONE |
10.6000 |
2.0150 |
n-octane |
OCTANE |
1.9406 |
1.9527 |
1-octanol |
OCTANOL |
9.8629 |
2.0435 |
2-octanone |
OCTANON2 |
9.4678 |
2.0025 |
n-pentadecane |
PENTDECN |
2.0333 |
2.0492 |
pentanal |
PENTANAL |
10.0000 |
1.9444 |
n-pentane |
NPENTANE |
1.8371 |
1.8428 |
pentanoic acid |
PENTACID |
2.6924 |
1.9839 |
1-pentanol |
PENTANOL |
15.1300 |
1.9884 |
2-pentanone |
PENTNON2 |
15.2000 |
1.9307 |
3-pentanone |
PENTNON3 |
16.7800 |
1.9388 |
1-pentene |
PENTENE |
1.9905 |
1.8810 |
E-2-pentene |
E2PENTEN |
2.0510 |
1.9025 |
pentyl acetate |
PENTACET |
4.7297 |
1.9664 |
pentylamine |
PENTAMIN |
4.2010 |
2.0967 |
perfluorobenzene |
PFB |
2.0290 |
1.8981 |
phenylmethanol |
BENZALCL |
12.4570 |
2.3704 |
propanal |
PROPANAL |
18.5000 |
1.8594 |
propanoic acid |
PROPACID |
3.4400 |
1.9235 |
1-propanol |
PROPANOL |
20.5240 |
1.9182 |
2-propanol |
PROPNOL2 |
19.2640 |
1.8978 |
propanonitrile |
PROPNTRL |
29.3240 |
1.8646 |
2-propen-1-ol |
PROPENOL |
19.0110 |
1.9980 |
propyl acetate |
PROPACET |
5.5205 |
1.9160 |
propylamine |
PROPAMIN |
4.9912 |
1.9238 |
pyridine |
PYRIDINE |
12.9780 |
2.2786 |
tetrachloroethene |
C2CL4 |
2.2680 |
2.2659 |
tetrahydrofuran |
THF |
7.4257 |
1.9740 |
tetrahydrothiophene-s,s-dioxide |
SULFOLAN |
43.9620 |
2.2002 |
tetralin |
TETRALIN |
2.7710 |
2.3756 |
thiophene |
THIOPHEN |
2.7270 |
2.3375 |
thiophenol |
PHSH |
4.2728 |
2.5259 |
toluene |
TOLUENE |
2.3741 |
2.2383 |
tributyl phosphate |
TBP |
8.1781 |
2.0232 |
1,1,1-trichloroethane |
TCA111 |
7.0826 |
2.0676 |
1,1,2-trichloroethane |
TCA112 |
7.1937 |
2.1650 |
trichloroethene |
TCE |
3.4220 |
2.1824 |
triethylamine |
ET3N |
2.3832 |
1.9628 |
2,2,2-trifluoroethanol |
TFE222 |
26.7260 |
1.6659 |
1,2,4-trimethylbenzene |
TMBEN124 |
2.3653 |
2.2644 |
2,2,4-trimethylpentane |
ISOCTANE |
1.9358 |
1.9363 |
n-undecane |
UNDECANE |
1.9910 |
2.0730 |
m-xylene |
M-XYLENE |
2.3478 |
2.2416 |
o-xylene |
O-XYLENE |
2.5454 |
2.2665 |
p-xylene |
P-XYLENE |
2.2705 |
2.2374 |
xylene (mixture) |
XYLENEMX |
2.3879 |
2.2485 |
1,1-dichloroethane |
10.1900 |
2.0880 |
|
1-iodopentene |
5.7800 |
2.2350 |
|
1-pentyne |
2.0600 |
1.9182 |
|
2-chlorobutane |
8.3900 |
1.9656 |
|
benzyl alcohol |
11.9200 |
2.3716 |
|
bromooctane |
5.0200 |
2.1083 |
|
butyl ethanoate |
5.0700 |
1.9432 |
|
butyl benzene |
2.3600 |
2.2201 |
|
carbon tet |
2.2300 |
2.1316 |
|
chlorotoluene |
6.8500 |
2.3654 |
|
decalin |
2.1900 |
2.1934 |
|
dimethylacetamide |
DMAC |
37.7800 |
2.0678 |
dimethylformamide |
DMF |
37.2200 |
2.0478 |
dimethylpyridine |
7.1700 |
2.2350 |
|
dodecane |
2.0100 |
2.0221 |
|
E-1,2-dichloroethene |
2.1400 |
2.0880 |
|
ethyl ethanoate |
6.0800 |
1.8824 |
|
ethyl methanoate |
8.3300 |
1.8469 |
|
ethyl eneglycol |
40.2500 |
2.0506 |
|
hexadecyl iodide |
3.5300 |
2.1934 |
|
hexanoic |
2.6000 |
2.0051 |
|
isobutanol |
16.7800 |
1.9460 |
|
isopropyl ether |
3.8800 |
1.8714 |
|
isopropyl toluene |
2.2300 |
2.2231 |
|
methyl ethanoate |
6.8600 |
1.8523 |
|
methyl methanoate |
8.8400 |
1.8036 |
|
methyl phenyl ketone |
17.4400 |
2.3624 |
|
methylformamide |
181.5600 |
2.0506 |
|
hexadecane |
2.0600 |
2.0592 |
|
methylaniline |
5.9600 |
2.4649 |
|
pentane |
1.8400 |
1.8414 |
|
pentadecane |
2.0300 |
2.0478 |
|
pentyl ethanoate |
4.7300 |
1.9656 |
|
phenyl ether |
3.7300 |
2.4932 |
|
propyl ethanoate |
5.5200 |
1.9155 |
|
pyrrolidine |
8.0400 |
2.0822 |
|
sec-butanol |
15.9400 |
1.9544 |
|
t-butanol |
12.4700 |
1.9238 |
|
t-butylbenzene |
2.3400 |
2.2290 |
|
tetrahyrothiophenedioxide |
43.9600 |
2.1993 |
|
tribromomethane |
4.2500 |
2.5632 |
|
trichloromethane |
TCM |
4.7100 |
2.0909 |
Z-1,2-dichloroethene |
9.2000 |
2.0996 |
|
isoquinoline |
11.0000 |
1.0100 |
|
quinoline |
9.1600 |
1.0100 |
|
diethylether |
4.2400 |
1.8295 |
|
dichloroethane |
10.1250 |
2.0874 |
|
carbontetrachloride |
2.2280 |
2.1319 |
|
heptane |
1.9113 |
1.9260 |
|
dimethylsulfoxide |
46.8260 |
2.0079 |
|
argon |
1.4300 |
1.4300 |
|
krypton |
1.5190 |
1.5190 |
|
xenon |
1.7060 |
1.7060 |
|
n-octanol |
9.8629 |
2.0435 |
|
aceticacid |
6.2528 |
1.8824 |
|
a-chlorotoluene |
6.7175 |
2.3688 |
|
benzylalcohol |
12.4570 |
2.3704 |
|
butanoicacid |
2.9931 |
1.9544 |
|
butylethanoate |
4.9941 |
1.9435 |
|
carbondisulfide |
2.6105 |
2.6631 |
|
decalin-mixture |
2.1960 |
2.1106 |
|
dibutylether |
3.0473 |
1.9578 |
|
diethylsulfide |
5.7230 |
2.0822 |
|
diisopropylether |
3.3800 |
1.8712 |
|
dimethyldisulfide |
9.6000 |
2.3375 |
|
diphenylether |
3.7300 |
2.4923 |
|
E-1,2-dichloroethene |
2.1400 |
2.0892 |
|
E-2-pentene |
2.0510 |
1.9025 |
|
ethylethanoate |
5.9867 |
1.8832 |
|
ethylmethanoate |
8.3310 |
1.8493 |
|
ethylphenylether |
4.1797 |
2.2729 |
|
formicacid |
51.1000 |
1.8807 |
|
hexanoicacid |
2.6000 |
2.0059 |
|
methylbenzoate |
6.7367 |
2.2995 |
|
methylbutanoate |
5.5607 |
1.9260 |
|
methylethanoate |
6.8615 |
1.8534 |
|
methylmethanoate |
8.8377 |
1.8045 |
|
methylpropanoate |
6.0777 |
1.8975 |
|
n-methylaniline |
5.9600 |
2.4599 |
|
n-methylformamide-mixture |
181.5600 |
2.0503 |
|
n,n-dimethylacetamide |
37.7810 |
2.0678 |
|
n,n-dimethylformamide |
37.2190 |
2.0463 |
|
pentanoicacid |
2.6924 |
1.9839 |
|
pentylethanoate |
4.7297 |
1.9664 |
|
propanoicacid |
3.4400 |
1.9235 |
|
propylethanoate |
5.5205 |
1.9160 |
|
tetrahydrothiophene-s,s-dioxide |
43.9620 |
2.2002 |
|
tributylphosphate |
8.1781 |
2.0232 |
|
xylene-mixture |
2.3879 |
2.2485 |
|
Z-1,2-dichloroethene |
9.2000 |
2.0996 |
点电荷模型
BDF支持将MM区原子电荷作为点电荷输入进行计算。点电荷以与计算任务同名的 $BDFTASK.extcharge 文件作为输入,具体格式如下:
$COMPASS
Title
water molecule in backgroud of exteral charges
Basis
6-31g
Geometry
O 0.000000 0.000000 0.106830
H 0.000000 0.785178 -0.427319
H 0.000000 -0.785178 -0.427319
End Geometry
Extcharge #表示需要输入点电荷
point #表示输入电荷类型为点电荷
$END
$XUANYUAN
$END
$SCF
RHF
$END
点电荷输入文件(文件名 h2o.extcharge)如下:
External charge, Point charge #第一行为标题和说明行
6 #要输入的点电荷数
C1 -0.732879 0.000000 5.000000 0.114039
C2 0.366440 0.000000 5.780843 -0.456155
C3 0.366440 0.000000 4.219157 -0.456155
C4 -0.732879 0.000000 10.00000 0.114039
C5 0.366440 0.000000 10.78084 -0.456155
C6 0.366440 0.000000 9.219157 -0.456155
点电荷的默认输入格式为: 原子标签、 电荷、 和坐标( x y z) ; 坐标单位默认为埃。坐标输入单位也可以为Bohr,输入格式如下:
External charge, Point charge # title line
6 Bohr # Unit: Bohr
C1 -0.732879 0.000000 5.000000 0.114039
# 省略 #
波函数分析和性质分析
BDF支持的波函数分析有:Mulliken布居分析和Lowdin布居分析,包括原子净电荷和原子自旋密度。
BDF支持的单电子性质有:
SCF:偶极矩,极化率*,超极化率*,穆斯堡尔谱(有效接触密度、电场梯度),核磁共振**
TDDFT:激发态的偶极矩*,荧光吸收光谱的振子强度,磷光吸收光谱的振子强度
* 在
resp模块中计算。** 在nmr模块中计算。
更多的波函数分析及单电子性质,可以通过在 scf 模块中产生molden格式的数据文件,用第三方程序完成。输入示例:
$scf
rks
dft
b3lyp
molden
$end
标准的molden格式仅支持spdfg型高斯基函数,但在BDF中已推广到h函数。
借助第三方程序LModeA-nano或LModeA,还可以对BDF的振动频率计算结果进行局域振动模式分析,并为分子力学计算提取内坐标的力常数。
有效接触密度
计算有效接触密度(ED)需要同时考虑相对论效应(在BDF中用X2C哈密顿,通过 heff =21,22,或23指认)
和有限尺寸的原子核( nuclear =1)。在sf-X2C-AU/B3LYP级别的输入示例如下:
$xuanyuan
heff
23
nuclear
1
$end
$scf
rks
dft
b3lyp
grid
ultra fine
reled
20
$end
其中,reled 调用相对论性质ED的计算,20 表示对原子序数小于20的轻元素不计算ED,从而节省计算时间。
对于密度泛函计算,ED的值对积分格点比较敏感,建议用精密的 ultra fine 。
ED需要对基组进行特殊处理,见 穆斯堡尔谱 。
电场梯度
计算电场梯度(EFG)的要求与ED类似,关键词为 relefg 。见 穆斯堡尔谱 。
molden2aim
下载: https://github.com/zorkzou/Molden2AIM
molden2aim的用途是把BDF产生的molden文件转化为wfn,wfx,或NBO-47格式的数据文件,用于各种分析。支持spdfgh型高斯基函数以及ECP。
Multiwfn
下载: http://sobereva.com/multiwfn/
Multiwfn是功能强大的波函分析程序。通过BDF产生的molden数据文件(支持spdfgh基函数和赝势)或经molden2aim转化的wfn、wfx数据文件, 可以用Multiwfn进行各种波函数分析,例如电子密度拓扑分析(也称 分子中原子的量子理论 ;QTAIM),电子局域函数(ELF),布居分析, 键级分析,原子电荷分析,等,也可以绘制分子轨道、电子密度和各种实空间函数的图像。 细节参见Multiwfn使用手册。
NBO分析
BDF目前不包含NBO( https://nbo7.chem.wisc.edu/ )的接口,但是可以利用molden2aim,把BDF产生的molden文件(支持spdfgh基函数和赝势)转化为NBO-47格式的数据文件, 再利用NBO独立程序gennbo.exe进行NBO分析。
对于RHF/RKS和UHF/UKS类型的波函数(即,MO占据数只能是0,1,2三种),NBO可以计算“Second Order Perturbation Theory Analysis”,这需要在47文件中出现Fock矩阵。
为此需要在molden2aim的配置文件 m2a.ini 中设置 nbopro=1 。
力常数
LModeA-nano(https://lmodea-nano.readthedocs.io/en/latest/)是PyMOL插件,用于固体和分子的局域振动模式分析, 计算化学键、键长、键角的力常数和谐振频率。 中文介绍见:http://bbs.keinsci.com/thread-28658-1-1.html
BDF振动频率计算任务产生的.umv数据文件可以直接被LModeA-nano程序读取。